【树状数组 离散化】bzoj1573: [Usaco2009 Open]牛绣花cowemb

解方程题！

Description

Bessie学会了刺绣这种精细的工作。牛们在一片半径为d(1 <= d <= 50000)的圆形布上绣花. 它们一共绣了N (2 <= N <= 50000)条直线，每条直线连接布的边缘上的两个点(没有两条线通过边上同一个点)。 作为一只热爱数学的牛，Bessie 知道每条线的公式, ax + by + c = 0. a, b, 和 c 为整数(-1000000 <= a <= 1000000; -1000000 <= b <= 1000000; -1000000 <= c <= 1000000).没有两条线完全重合。 不幸的是, 一部分线不通过圆布的内部. 原点(0,0)在布的正中央, 所有边上的点离原点距离为d. 每条线的公式满足至少a,b中的一个非零. 对于牛来说，刺绣作品中线的交点越多，便越有价值。帮助Bessie计算在圆中相交的线的对数，也就是说交点与原点的距离小于d。注意如果三条线在圆内同一点相交,这算3对线。4线共点->6对线.

Input

第1行: 两个空格分开的数, N 和 d 第2..N+1行: 第 i+1 行包含第i条线的参数: a, b 和 c

Output

第1行: 一行，包含一个数,为在园内相交的线的对数.

Sample Input

2 1
1 0 0
0 1 0

输入说明：
两条直线x=0和y=0.

Sample Output

1

HINT

两条线在(0,0)相交, 明显离原点距离小于1.

---

题目分析

模型转化

$n=50000$的数据规模，$n^2$的枚举肯定不行。那么可以省去哪些枚举呢？

先考虑哪些线段才会相交。

因为对于一条直线，有效部分就只有与圆内的公共部分。所以我们只需要记录直线与圆的两个交点。

但是由于会出现如下图所示情况，

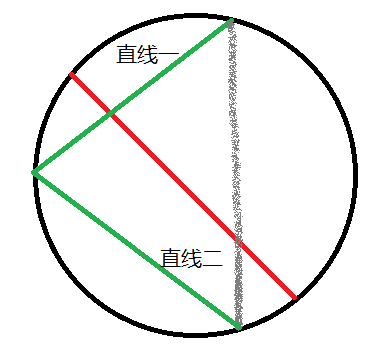
还需要把x轴坐标再映射一下。若$y<0$，则$L=-x-r$；反之$R=x+r$。

自然发现这样映射之后，圆上任意一点都有了唯一的映射值。

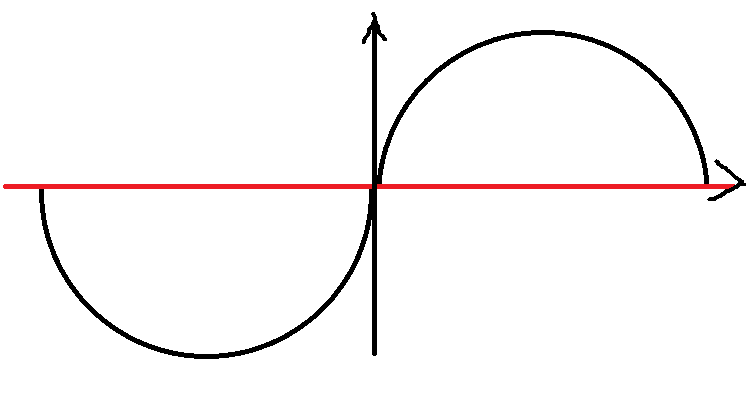
实际上就是变成了这样。

于是直线在圆内相交就等价于映射后的线段下相交（不包含）。

树状数组维护

如何处理相交但不包含的线段条数？

这里有一种挺妙的方法：先把线段按照左端点排序，这样保证了处理时左端点的有序。然后计算线段内的右端点个数。因为之前处理的线段左端点都是小于等于现在处理的左端点的，所以线段内的右端点个数就是与现在处理的线段的相交的线段条数。

这样子就可以离散化后用树状数组做了。

（树状数组好棒啊！）

 #include<bits/stdc++.h>
 const int maxn = ;

 int n,d,cnt;
 long long f[maxn<<],ans;
 double t[maxn<<],xa,xb,ya,yb,a,b,c;
 std::pair<double, double> mp[maxn];

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 int lowbit(int x){return x&-x;}
 void add(int x){for (; x<maxn<<; x+=lowbit(x)) f[x]++;}
 int query(int x)
 {
     int ret = ;
     for (; x; x-=lowbit(x)) ret += f[x];
     return ret;
 }
 double calc(double x, double y){return y < ?-x-d:x+d;}
 int main()
 {
     n = read(), d = read();
     for (int i=; i<=n; i++)
     {
         // int a = read(), b = read(), c = read();
         scanf("%lf%lf%lf",&a,&b,&c);
         bool cte = ;
         xa = xb = ya = yb = ;
         if (!a || !b){
             if (!a){
                 double h = -c/b;
                 if (h*h-d*d > ) cte = ;
                 else{
                     xa = -sqrt(d*d*1.0-h*h), xb = -xa;
                     ya = yb = h;
                 }
             }else{
                 double w = -c/a;
                 if (w*w-d*d > ) cte = ;
                 else{
                     xa = xb = w;
                     ya = sqrt(d*d*1.0-w*w), yb = -ya;
                 }
             }
         }else{
             double equa = a*a+b*b*1.0, equb = *a*c*1.0, equc = c*c*1.0-b*b*d*d*1.0;
             double delta = equb*equb*1.0-4.0*equa*equc;
             if (delta < ) cte = ;
             else{
                 xa = (-equb-sqrt(delta))/(2.0*equa);
                 xb = (-equb+sqrt(delta))/(2.0*equa);
                 ya = -(a*xa+c)/b;
                 yb = -(a*xb+c)/b;
             }
         }
         if (cte) continue;
         double L = calc(xa, ya), R = calc(xb, yb);
         if (L > R) std::swap(L, R);
         mp[++cnt] = std::make_pair(L, R);
         t[cnt*-] = L, t[cnt*] = R;
     }
     std::sort(mp+, mp+cnt+);
     std::sort(t+, t+*cnt+);
     for (int i=; i<=cnt; i++)
     {
         int x = std::lower_bound(t+, t+*cnt+, mp[i].first)-t;
         int y = std::lower_bound(t+, t+*cnt+, mp[i].second)-t;
         ans += query(y)-query(x-);
         add(y);
     }
     printf("%lld\n",ans);
     return ;
 }

END