cf287E Main Sequence

As you know, Vova has recently become a new shaman in the city of Ultima Thule. So, he has received the shaman knowledge about the correct bracket sequences. The shamans of Ultima Thule have been using lots of different types of brackets since prehistoric times. A bracket type is a positive integer. The shamans define a correct bracket sequence as follows:

• An empty sequence is a correct bracket sequence.
• If {a₁, a₂, ..., a_l} and {b₁, b₂, ..., b_k} are correct bracket sequences, then sequence {a₁, a₂, ..., a_l, b₁, b₂, ..., b_k} (their concatenation) also is a correct bracket sequence.
• If {a₁, a₂, ..., a_l} — is a correct bracket sequence, then sequence 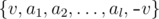also is a correct bracket sequence, where v (v > 0) is an integer.

For example, sequences {1, 1,  - 1, 2,  - 2,  - 1} and {3,  - 3} are correct bracket sequences, and {2,  - 3} is not.

Moreover, after Vova became a shaman, he learned the most important correct bracket sequence {x₁, x₂, ..., x_n}, consisting of n integers. As sequence x is the most important, Vova decided to encrypt it just in case.

Encrypting consists of two sequences. The first sequence {p₁, p₂, ..., p_n} contains types of brackets, that is, p_i = |x_i| (1 ≤ i ≤ n). The second sequence {q₁, q₂, ..., q_t} contains t integers — some positions (possibly, not all of them), which had negative numbers in sequence {x₁, x₂, ..., x_n}.

Unfortunately, Vova forgot the main sequence. But he was lucky enough to keep the encryption: sequences {p₁, p₂, ..., p_n} and {q₁, q₂, ..., q_t}. Help Vova restore sequence x by the encryption. If there are multiple sequences that correspond to the encryption, restore any of them. If there are no such sequences, you should tell so.

Input

The first line of the input contains integer n (1 ≤ n ≤ 10⁶). The second line contains n integers: p₁, p₂, ..., p_n (1 ≤ p_i ≤ 10⁹).

The third line contains integer t (0 ≤ t ≤ n), followed by t distinct integers q₁, q₂, ..., q_t (1 ≤ q_i ≤ n).

The numbers in each line are separated by spaces.

Output

Print a single string "NO" (without the quotes) if Vova is mistaken and a suitable sequence {x₁, x₂, ..., x_n} doesn't exist.

Otherwise, in the first line print "YES" (without the quotes) and in the second line print n integers x₁, x₂, ..., x_n (|x_i| = p_i; x_qj < 0). If there are multiple sequences that correspond to the encrypting, you are allowed to print any of them.

Examples

Input

2
1 1
0

Output

YES
1 -1

Input

4
1 1 1 1
1 3

Output

YES
1 1 -1 -1

Input

3
1 1 1
0

Output

NO

Input

4
1 2 2 1
2 3 4

Output

YES
1 2 -2 -1

题意是有1e9种括号，每种括号的左括号用k表示，右括号用-k表示，现在给出个序列，其中已知一些括号是右括号，可以再把一些左括号变右括号（正数取反）要找到一种括号匹配的方式

从后往前找，维护一个栈，如果当前的括号跟栈顶的匹配就马上匹配，否则改负号扔进栈里去。

如果当前这个括号跟栈顶的匹配，而你又选择不匹配的话，那么这个括号和栈顶都要分别再和后面的某个相同的括号匹配。

如果再后面的括号也真的存在，那么完全可以当前的和栈顶匹配，后面的自己匹配，所以当前和栈顶匹配这里也是可行的。如果后面的不存在，这样无解，只能当前的和栈顶匹配。所以当前的跟栈顶的能匹配就匹配。

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<algorithm>
 #include<cmath>
 #include<queue>
 #include<deque>
 #include<set>
 #include<map>
 #include<ctime>
 #define LL long long
 #define inf 0x7ffffff
 #define pa pair<int,int>
 #define mkp(a,b) make_pair(a,b)
 #define pi 3.1415926535897932384626433832795028841971
 using namespace std;
 inline LL read()
 {
     LL x=,f=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 int n,m;
 int a[];
 int zhan[],top;
 int main()
 {
     n=read();
     for (int i=;i<=n;i++)a[i]=read();
     m=read();
     for (int i=;i<=m;i++)a[read()]*=-;
     for (int i=n;i>=;i--)
     {
         if (a[i]<)zhan[++top]=i;
         else if (top&&a[i]+a[zhan[top]]==)top--;
         else if (top&&a[i]==a[zhan[top]])a[i]*=-,top--;
         else a[i]*=-,zhan[++top]=i;
     }
     if (top)puts("NO");
     else {puts("YES");for (int i=;i<=n;i++)printf("%d ",a[i]);}
 }

cf 287E