51nod 1285 山峰和分段

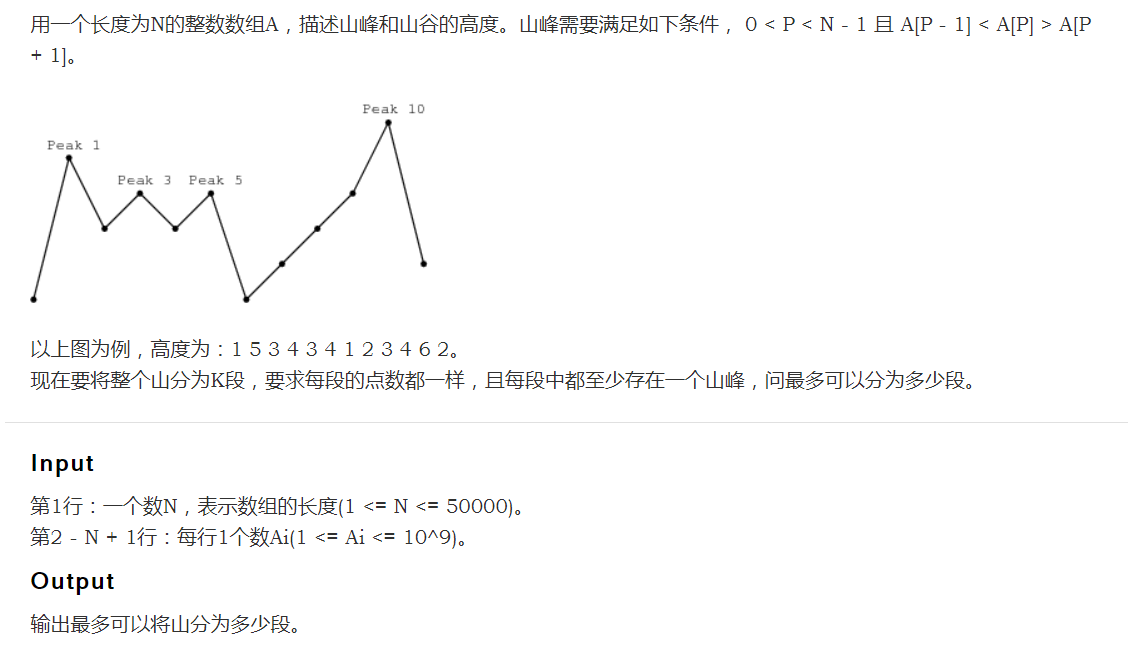
【题解】

　　枚举n的各个因数作为段长，O(n)判断每一段内是否有山峰即可。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 #define LL long long
 #define rg register
 #define N 1000010
 using namespace std;
 int n,m,ans,a[N];
 bool p[N];
 inline int read(){
     int k=,f=; char c=getchar();
     while(c<''||c>'')c=='-'&&(f=-),c=getchar();
     while(''<=c&&c<='')k=k*+c-'',c=getchar();
     return k*f;
 }
 inline bool check(int x){
     int last=,now=x;
     while(now<=n){
         bool ok=;
         for(rg int i=last;i<=now;i++) ok=ok|p[i];
         if(!ok) return ;
         now+=x; last+=x;
     }
     return ;
 }
 int main(){
     n=read(); m=trunc(sqrt(n));
     for(rg int i=;i<=n;i++) a[i]=read();
     for(rg int i=;i<n;i++) if(a[i-]<a[i]&&a[i]>a[i+]) p[i]=;
     for(rg int i=;i<=m;i++)if(n%i==){
         if(check(i)) ans=max(ans,n/i);
         if(check(n/i)) ans=max(ans,i);
     }
     printf("%d\n",ans);
     return ;
 }