Codeforces Round #646 (Div. 2)【C. Game On Leaves 题解】

题意分析

关于这道题，意思就是两个人摘叶子，谁最后摘到编号为x的谁就赢了。既然是叶子，说明其最多只有一个分支，由于题目上说了是无向图，那就是度数小于等于的节点。也就是一步步移除度数小于等于的节点，直到将编号为的节点删掉游戏才结束。

那么我们可以将x这个节点作为根节点，初始时这棵树的样子如下:



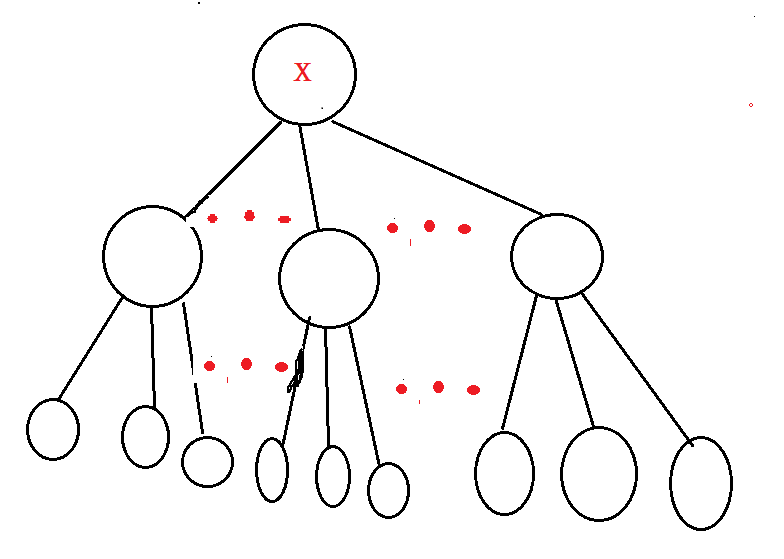
两个人摘来摘去，谁也不想让对方赢，最终的结果必然是这个样子。（这是当节点总数大于等于3的情况）



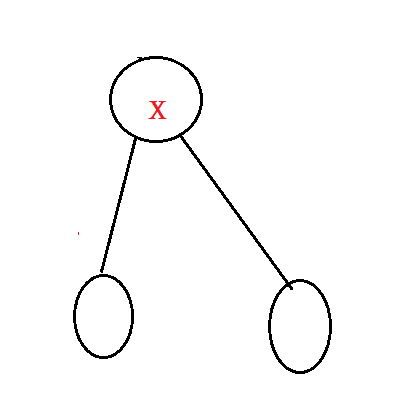
这样我们就不难发现，当节点总数n大于等于3时，若n-3为偶数，那么最终肯定是后摘的那个人赢；反之就是先摘的那个人赢；

当节点总数n小于3时，那一定是先摘的那个人赢。

分析完了，下面看代码。

代码

#include<iostream>
using namespace std;
int t, n, x, u, v;
int main()
{
    cin >> t;
    while(t--)
    {
        cin >> n >> x;
        int degree = 0;         //x这个节点的度数
        for(int i = 0; i < n - 1;i ++)      //注意这里，是n-1行
        {
            cin >> u >> v;
            if(u == x || v == x)        //由于题目中说不会有环，故此处直接这样判断
                degree++;
        }
        if(degree <= 1)         //度数为1，肯定先开始的先赢
            puts("Ayush");
        else
        {
            if((n - 3) % 2 == 0)
                puts("Ashish");
            else
                puts("Ayush");
        }

    }
    return 0;
}