[poj1062][最短路]昂贵的聘礼

（最近总是有想让我的小博客更加充实的冲动，遇见一个不平常的题就想写下来。今天这个题姑且算是同学推荐的好题，很有意思，志之）

题目

题面

年轻的探险家来到了一个印第安部落里。在那里他和酋长的女儿相爱了，于是便向酋长去求亲（哪里都有想桃子的人）。酋长要他用10000个金币作为聘礼才答应把女儿嫁给他。探险家拿不出这么多金币，便请求酋长降低要求。酋长说："嗯，如果你能够替我弄到大祭司的皮袄，我可以只要8000金币。如果你能够弄来他的水晶球，那么只要5000金币就行了。"探险家就跑到大祭司那里，向他要求皮袄或水晶球，大祭司要他用金币来换，或者替他弄来其他的东西，他可以降低价格。探险家于是又跑到其他地方，其他人也提出了类似的要求，或者直接用金币换，或者找到其他东西就可以降低价格。不过探险家没必要用多样东西去换一样东西，因为不会得到更低的价格。探险家现在很需要你的帮忙，让他用最少的金币娶到自己的心上人。另外他要告诉你的是，在这个部落里，等级观念十分森严。地位差距超过一定限制的两个人之间不会进行任何形式的直接接触，包括交易。他是一个外来人，所以可以不受这些限制。但是如果他和某个地位较低的人进行了交易，地位较高的的人不会再和他交易，他们认为这样等于是间接接触，反过来也一样。因此你需要在考虑所有的情况以后给他提供一个最好的方案。
为了方便起见，我们把所有的物品从1开始进行编号，酋长的允诺也看作一个物品，并且编号总是1。每个物品都有对应的价格P，主人的地位等级L，以及一系列的替代品Ti和该替代品所对应的"优惠"Vi。如果两人地位等级差距超过了M，就不能"间接交易"。你必须根据这些数据来计算出探险家最少需要多少金币才能娶到酋长的女儿。

输入第一行是两个整数M，N（1 <= N <=
100），依次表示地位等级差距限制和物品的总数。接下来按照编号从小到大依次给出了N个物品的描述。每个物品的描述开头是三个非负整数P、L、X（X
< N），依次表示该物品的价格、主人的地位等级和替代品总数。接下来X行每行包括两个整数T和V，分别表示替代品的编号和"优惠价格"。

输出最少需要的金币数。

Sample Input

1 4

10000 3 2

2 8000

3 5000

1000 2 1

4 200

3000 2 1

4 200

50 2 0

Sample Output

5250

解说

先说一下大体的思路。这里等级是一个比较特殊的新东西，先不看它，那么一切就会变得极其简单。既然有物品的权值，那么一般来说会需要超级源点（且叫做0号）作为起点。每个物品原本的价值就是从源点到这个物品建一条边。而每个物品的替代品就是从这个替代品到这个物品建一条边，代表买了替代品再花多少钱就能买下目标物品。那么这样的话，最后要花的钱就是从0号点到酋长点（1号节点）的距离最短距离，用什么算法跑都无所谓，毕竟不涉及环（稍微解释一下为什么不涉及环：因为不合实际！我要娶你的女儿，那要魔法球；我要魔法球，那需要皮袄；我要皮袄，那么需要酋长的女儿……就像一个梗：我要来贵公司上班；抱歉不行，因为您没有工作经历；我还没有找到工作哪里来的工作经历？；那您就去找工作啊！；这就是我来这里的原因！……没完了，不是吗？）和负边。下面展示一下样例的图。

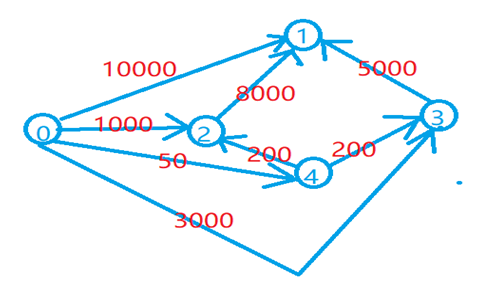
接下来看看等级是个啥。

仔细琢磨一下等级的定义，有几个要注意的点：

1.酋长不一定是最高等级（篡权啦！朕的大清要亡了！！！很不现实但就是这样）

2.由于上述第一点，最大等级差就是交易的人中最高等级与最低等级的差，而非酋长与最低等级的差。

3.交易的人中涉及的最高等级与最低等级之间一定要包含酋长等级。

这样的话，我们就枚举所有可能的等级区间就好了，若酋长等级为level[1]，允许的等级差为m，那么我就枚举[level[1]-m,level[1]]到[level[1],level[1]+m]每一个区间，分别求0到1的最短路，求的时候只要到达点的level不在区间里就直接continue掉。最后求一下最小值就行。

代码

（最短路用的迪杰特斯拉）

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<queue>
 #include<stack>
 #include<algorithm>
 using namespace std;
 const int maxn=+;
 int m,n,tot,ans,head[maxn],dis[maxn],level[maxn];
 struct edge{
     int to,next,len;
 }e[maxn+maxn*(maxn-)];
 void Add(int a,int b,int len){
     e[tot].len=len;
     e[tot].to=b;
     e[tot].next=head[a];
     head[a]=tot;
     tot++;
 }
 struct node{
     int num,dis;
     node(int x,int y){
         num=x;
         dis=y;
     }
     bool operator<(const node &a) const{
         return dis>a.dis;
     }
 };
 void dijs(int l,int r){
     priority_queue<node> q;
     bool f[maxn];
     memset(f,,sizeof(f));
     memset(dis,0x3f,sizeof(dis));
     dis[]=;
     q.push(node(,));
     while(!q.empty()){
         node p=q.top();q.pop();
         int k=p.num;
         if(f[k]) continue;
         f[k]=;
         for(int i=head[k];i;i=e[i].next){
             int u=e[i].to;
             if(level[u]<l||level[u]>r) continue;
             int len;
             len=dis[k]+e[i].len;
             if(len<dis[u]){
                 dis[u]=len;
                 q.push(node(u,len));
             }
         }
     }
 }
 int main(){
     scanf("%d%d",&m,&n);
     tot=; ans=0x3f3f3f3f;
     for(int i=;i<=n;i++){
         int p,x;
         scanf("%d%d%d",&p,&level[i],&x);
         Add(,i,p);
         for(int j=;j<=x;j++){
             int to,len;
             scanf("%d%d",&to,&len);
             Add(to,i,len);
         }
     }
     for(int i=level[]-m;i<=level[];i++){
         dijs(i,i+m);
         ans=min(ans,dis[]);
     }
     printf("%d",ans);
     return ;
 } 

幸甚至哉，歌以咏志。