题目分享E 二代目

题意：一棵点数为n的树，每个节点有点权，要求在树中中找到一个最小的x，使得存在一个点满足max(该点点权，该点相邻的点的点权+1，其他点的点权+2)=x

分析：首先要能把题目转化为上述题意

　　首先题目让你选取一个点为根节点，

　　然后断掉这个点

　　让相邻的点与二次相邻的点的点权+1

　　然后剩下每次只能断掉与该点相邻的点，

　　断掉后处理与根节点断掉的处理一致

　　显然，对于任何一个根节点的儿子来说，他的权值一定只被+1

　　而对于其他节点来说，他的权值一定在他父亲断掉时和爷爷断掉时分别+1，也就是+2

那么我们现在转化完题目，现在剩下的题目其实就是个类似模拟的东西，不过还是有可聊之处的

　　首先，如果只有一个拥有最大点权的点，令该最大点权为maxa

　　　　那么显然一定要以这个节点为根节点，

　　　　因为如果不以该节点为根节点，那么最终结果至少为maxa+1

　　　　而如果以该节点为根节点，显然当点权为maxa-1的点位于根节点相邻以外的节点时，会使结果变成maxa+1，而且这是最坏情况

　　　　最坏情况与最好情况相同，显然要选该节点为根节点

　　那么求最终结果只需要dfs一下，将根节点的儿子+1，其余节点+2，最后在所有节点中求最大值即可

　　然后，如果有多个拥有最大点权的点呢？

　　很容易得到的不一定非要将根节点设在最大点权的点上，比如

　　

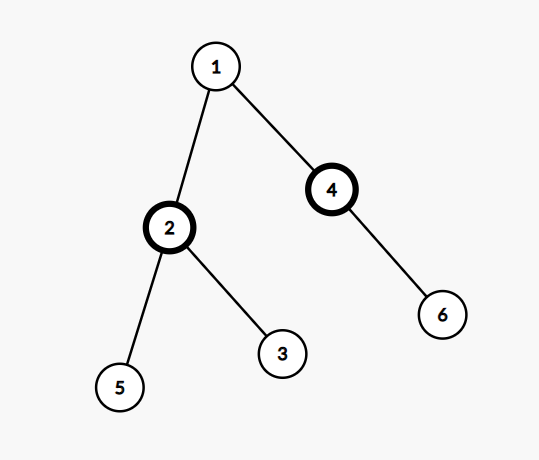
　　加粗的节点是最大点权的点

　　显然将根节点设在1一定比将根节点设在2或4更优

　　那么也很容易得到，当所有的最大点权的点都连在同一个点上时，才会出现maxa+1这种结果，比如

　　或

　　

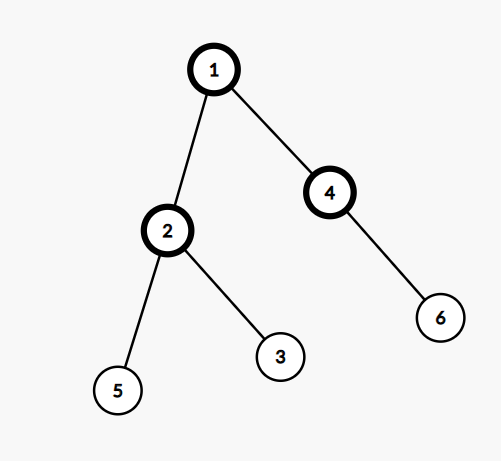
　　而如果不连在同一个节点上，则结果就是maxa+2，如

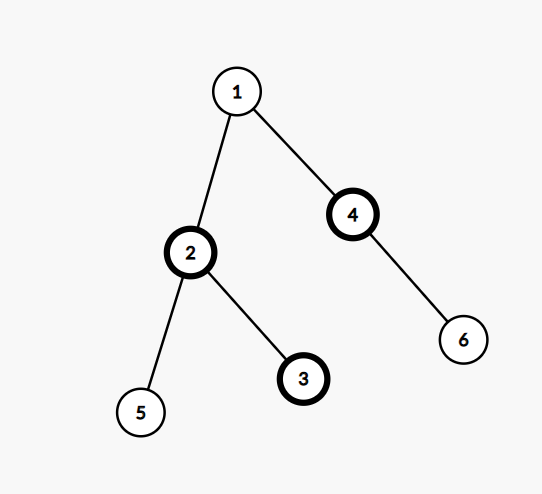
　　那么我们如何判断所有的最大点权的点是否连在同一个节点上呢？

　　最简单的方法肯定是直接用floyd之类的方法求出任意两个最大点权的点之间的距离

　　如果出现有一个距离>2,那么这两个点显然就不可能连在同一个节点上或相邻

　　如果没有出现，那么显然他们一定是连在同一个节点上的

　　那么这样的方法显然是超时的，

　　那么我们能不能省略几次呢？

　　首先如果我们只以其中任意一个节点为根，

　　用dfs求出其他节点到该节点的距离，

　　然后再判断是否存在>2的，

　　显然并不能得到我们想要的结果，比如

　　

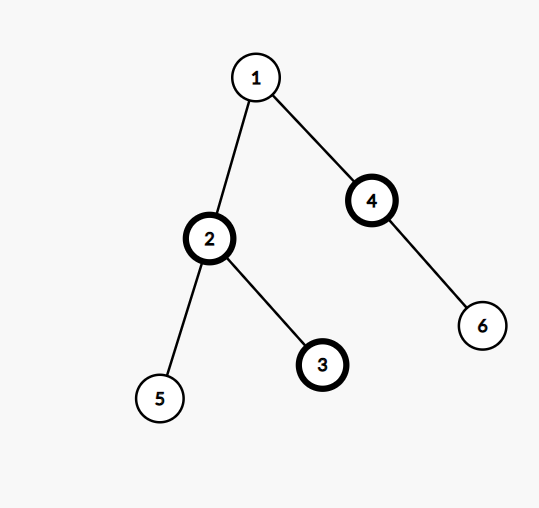
　　如果我选的是节点2，显然与正确答案不符

　　那么如果我任选两个可以吗

　　答案也是不行的，不过这个可能有点难想，比如这个

　　

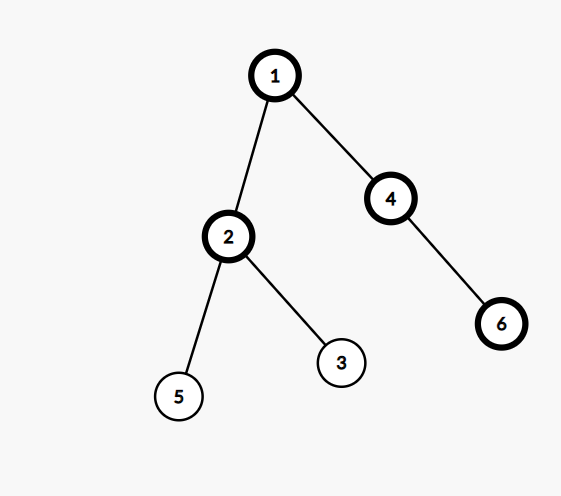
　　如果我选的是1,4，那么得到的结果就与答案不符

　　那么如果我选3个呢？

　　好像没找到反例，那怎么证明一定符合我们的要求呢？

　　　　首先，如果存在3个节点没出现距离大于二，那么他们两两之间距离一定小于等于2

　　　　那么他们只有两种可能

　　　　第一种是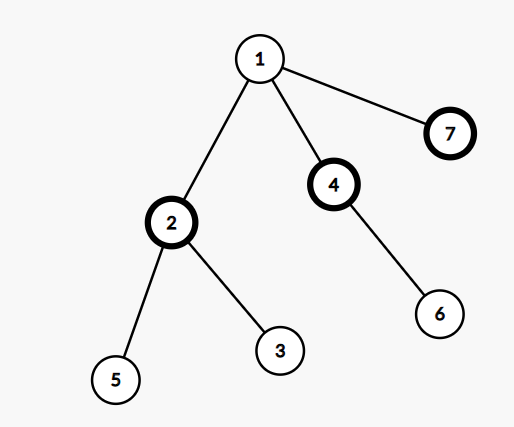

　　　　第二种是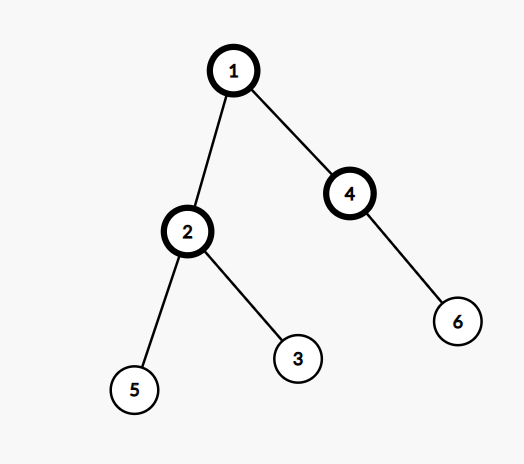

　　　　对于第一种来说，其实只需要两个节点保证没有出现距离大于2的节点就可以得到结果

　　　　　　考虑极端的等于2的情况，我对于任意一个根节点一定满足这个图

　　　　　　

　　　　　　而此时有两个节点满足该情况，如果出现5,6这种情况，显然就不可能出现两个节点满足该情况

　　　　　　所以也就是说只能出现这种情况

　　　　　　

　　　　　　显然这种情况一定是成立的

　　　　那么对于第二种情况来说，

　　　　　　

　　　　　　4会排除2子树中的干扰，2会排除4子树中的干扰，所以剩余的节点只能为1节点的儿子，从而得证

　　　　理一下，刚才较为冗长的证明证明了只需要任选三个最大权值节点dfs即可，这三个节点若找到一个与他们距离>2的最大权值节点，那么最终结果就是maxa+2，否则就是maxa+1

代码：

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;

const int maxn=3e5+;
const int inf=1e9+;

struct Node
{
    int to,next;
}e[maxn<<];
int head[maxn];
int len[maxn];
int a[maxn];
vector<int> q;
int cnt;

void add(int x,int y)
{
    e[++cnt].to=y;
    e[cnt].next=head[x];
    head[x]=cnt;
}

void dfs(int x,int fa)
{
    for(int i=head[x];i;i=e[i].next)
    {
        int v=e[i].to;
        if(v!=fa)
        {
            if(fa==-) a[v]++;
            else a[v]+=;
            dfs(v,x);
        }
    }
}

void dfslen(int x,int fa)
{
    for(int i=head[x];i;i=e[i].next)
    {
        int v=e[i].to;
        if(v!=fa)
        {
            len[v]=len[x]+;
            dfslen(v,x);
        }
    }
}

int chuli()
{
    for(int i=;i<min((int)q.size(),);i++)
    {
        len[q[i]]=;
        dfslen(q[i],-);
        for(int j=;j<q.size();j++) if(len[q[j]]>) return ;
    }
    return ;
}

int main()
{
    int n,x,y;
    scanf("%d",&n);
    int maxa=-inf;
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
        if(a[i]>maxa) maxa=a[i],q.clear(),q.push_back(i);
        else if(a[i]==maxa) q.push_back(i);
    }
    for(int i=;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        add(x,y),add(y,x);
    }
    if(q.size()==)
    {
        dfs(q[],-);
        for(int i=;i<=n;i++) maxa=max(maxa,a[i]);
        printf("%d",maxa);
    }
    else printf("%d",maxa+chuli());
    return ;
}