Miller Rabin算法判定质数(OI向)

　　前言:本篇不太适合那些对数学证明要求严格的Oier，然后本人也是蒟蒻，主要写给自己回顾用的

　　Miller Rabin算法能快速的判断一个数是否为质数，作为一个数学算法它具有一定的玄学成分，但是在OI中通过一些手段可以使其达到100%正确。

　　先让我们对比一下一般算法书教的2种关于质数的算法:

　　1,试除法，相比Miller Rabin它就是不够快，但是试除法的过程有很多好处，例如求其约数，这是Miller Rabin无法比拟的

　　 2,欧拉筛 ，求区间内质数，不是一条赛道的

　　先看复杂度：O(klog³n)

　　让我们开始吧！

　　首先我们明确Miller Rabin算法的原理，或者前置知识:费马小定理&二次探测定理

　　 费马小定理:a^p-1 Ξ 1 (mod p)大家应该不陌生,大部分算法书数学专题都有，而且今年(2024) 的九省联考压轴题也火了一把，没学过的先出门学下，费马小定理主要就用在本算法以及求逆元(同余相关)

　　二次探测定理我们好好介绍下:

　　对于一个质数p,若x² Ξ 1 (mod p)，则小于p的解有且仅有x = 1 或 x =  p - 1

　　为什么呢？(如下图，本人新手写博客  ，不太会数学公式，有点模糊将两4, 不过以后的我看应该没什么问题)

　　注意上述等式全是在mod p意义上的

　　以上知识在我如今看来是显然的，对于初学者的我当时却理解了一下午。。。所以各位加油

　　好，接下来让我们理一下思路

　　由费马小定理容易猜想如果，任取一组小于p的数为a，满足费马小定理形式p会是质数吗？

　　其实吧，我觉得大家学到这了应该容易想到不会的，我不作详细证明。举个反例561,显然这是3的倍数，但是你去按上文取数发现全都符合哦，我们把这些反例成为卡迈尔数

　　这个时候我们就要联系二次探测定理了，我们思考若p是个质数p - 1是不是个偶数啊，显然是(若p - 1 不是偶数，则为奇数对吧,则p为偶数,则一个偶数是质数,除了2都不满足啊，所以我们特判2然后把它当结论)

　　所以费马小定理可以表示成二次探测定理的形式：

　　　　　　　　

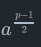　　然后就用到数学算法常用的分治了，如果，则我们把作为x²继续表示成二次探测定理的形式判断直到( p - 1) /2k(k为整数)变成奇数不能使用二次探测定理即可(其本质依然是通过尝试举反例来判断，所以存在玄学性)

　　综上，我们认为不违背二次探测定理的数即为质数，什么叫不违背? 后文和代码下次补，该睡觉了