第9讲、深入理解Scaled Dot-Product Attention

Scaled Dot-Product Attention是Transformer架构的核心组件，也是现代深度学习中最重要的注意力机制之一。本文将从原理、实现和应用三个方面深入剖析这一机制。

1. 基本原理

Scaled Dot-Product Attention的本质是一种加权求和机制，通过计算查询(Query)与键(Key)的相似度来确定对值(Value)的关注程度。其数学表达式为：

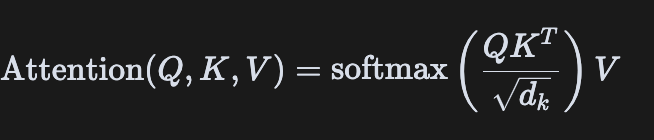
这个公式包含几个关键步骤：

计算相似度：通过点积(dot product)计算Query和Key的相似度，得到注意力分数(attention scores)
缩放(Scaling)：将点积结果除以$\sqrt{d_k}$进行缩放，其中$d_k$是Key的维度
应用Mask(可选)：在某些情况下（如自回归生成）需要遮盖未来信息
Softmax归一化：将注意力分数通过softmax转换为概率分布
加权求和：用这些概率对Value进行加权求和

2. 为什么需要缩放(Scaling)？

缩放是Scaled Dot-Product Attention区别于普通Dot-Product Attention的关键。当输入的维度$d_k$较大时，点积的方差也会变大，导致softmax函数梯度变得极小（梯度消失问题）。通过除以$\sqrt{d_k}$，可以将方差控制在合理范围内。

假设Query和Key的各个分量是均值为0、方差为1的独立随机变量，则它们点积的方差为$d_k$。通过除以$\sqrt{d_k}$，可以将方差归一化为1。

3. 代码实现解析

让我们看看PyTorch中Scaled Dot-Product Attention的典型实现：

def scaled_dot_product_attention(query, key, value, mask=None, dropout=None):

    # 获取key的维度

    d_k = query.size(-1)

    # 计算注意力分数并缩放

    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)

    # 应用mask（如果提供）

    if mask is not None:

        scores = scores.masked_fill(mask == 0, float('-inf'))

    # 应用softmax得到注意力权重

    attn = F.softmax(scores, dim=-1)

    # 应用dropout（如果提供）

    if dropout is not None:

        attn = dropout(attn)

    # 加权求和

    return torch.matmul(attn, value), attn

这个函数接受query、key、value三个张量作为输入，可选的mask用于遮盖某些位置，dropout用于正则化。

4. 张量维度分析

假设输入的形状为：

Query: [batch_size, seq_len_q, d_k]
Key: [batch_size, seq_len_k, d_k]
Value: [batch_size, seq_len_k, d_v]

计算过程中各步骤的维度变化：

Key转置后: [batch_size, d_k, seq_len_k]
Query与Key的点积: [batch_size, seq_len_q, seq_len_k]
Softmax后的注意力权重: [batch_size, seq_len_q, seq_len_k]
最终输出: [batch_size, seq_len_q, d_v]

5. 在Multi-Head Attention中的应用

Scaled Dot-Product Attention是Multi-Head Attention的基础。在Multi-Head Attention中，我们将输入投影到多个子空间，在每个子空间独立计算注意力，然后将结果合并：

class MultiHeadAttention(nn.Module):

    def __init__(self, h, d_model, dropout=0.1):

        super().__init__()

        assert d_model % h == 0

        self.d_k = d_model // h

        self.h = h

        self.linears = clones(nn.Linear(d_model, d_model), 4)

        self.attn = None

        self.dropout = nn.Dropout(dropout)

    def forward(self, query, key, value, mask=None):

        if mask is not None:

            mask = mask.unsqueeze(1)

        nbatches = query.size(0)

        # 1) 投影并分割成多头

        query, key, value = [

            l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)

            for l, x in zip(self.linears, (query, key, value))

        ]

        # 2) 应用注意力机制

        x, self.attn = scaled_dot_product_attention(query, key, value, mask, self.dropout)

        # 3) 合并多头结果

        x = x.transpose(1, 2).contiguous().view(nbatches, -1, self.h * self.d_k)

        return self.linears[-1](x)

6. 实际应用场景

Scaled Dot-Product Attention在多种场景下表现出色：

自然语言处理：捕捉句子中词与词之间的依赖关系
计算机视觉：关注图像中的重要区域
推荐系统：建模用户与物品之间的交互
语音处理：捕捉音频信号中的时序依赖

7. 优势与局限性

优势：

计算效率高（可以通过矩阵乘法并行计算）
能够捕捉长距离依赖关系
模型可解释性强（可以可视化注意力权重）

局限性：

计算复杂度为O(n²)，对于长序列计算开销大
没有考虑位置信息（需要额外的位置编码）
对于某些任务，可能需要结合CNN等结构以捕捉局部特征

8. 总结

Scaled Dot-Product Attention是现代深度学习中的关键创新，通过简单而优雅的设计实现了强大的表达能力。它不仅是Transformer架构的核心，也启发了众多后续工作，如Performer、Linformer等对注意力机制的改进。理解这一机制对于掌握现代深度学习模型至关重要。

通过缩放点积、应用softmax和加权求和这三个简单步骤，Scaled Dot-Product Attention成功地让模型"关注"输入中的重要部分，这也是它能在各种任务中取得卓越表现的关键所在。

9、Scaled Dot-Product Attention应用案例

敬请关注下一篇