斑点检测(LoG,DoG) [上]

维基百科，LoG，DoG，DoH

在计算机视觉中，斑点检测是指在数字图像中找出和周围区域特性不同的区域，这些特性包括光照或颜色等。一般图像中斑点区域的像素特性相似甚至相同，某种程度而言，斑点块中所有点是相似的。

如果将兴趣点的特性形式化表达为像素位置的函数，那么主要有两类斑点检测方法:

差分方法。这类方法主要基于函数在对应像素点处的导数。
局部极值方法。这类方法主要是在找出函数的局部极值。

在该领域中，斑点检测也被称为兴趣点检测或者兴趣区域检测。

研究斑点检测的目的有几点。其中最主要的是斑点检测能够完整的刻画像素所在区域信息，而这些信息是边缘检测和焦点检测所不能获得的。斑点检测获得的局部区域特征可以被用于后续进一步处理，比如在目标出现和部分遮挡的目标识别或追踪问题中准确刻画目标信息等。在其他领域，斑点检测还可以通过对直方图的尖峰检测实现分割。斑点检测子的另一个常见的应用是作为文本分析和识别中的基元。最新研究中，斑点检测越来越多的被应作图像宽基线立体匹配中的兴趣点检测和基于表观的目标识别中的局部图像特征。

这里主要介绍两种斑点检测方法--LoG和DoG。在介绍这两种斑点检测方法时，我们简单回顾下边缘检测方法--梯度算子和Laplacian算子。

边缘检测回顾

图像中的边缘一般分为两种：屋脊型边缘和阶跃型边缘，如下图是边缘剖面，纵坐标表示像素值

1474353422075.jpg

其中a,c子图是屋脊型边缘，向a那种函数趋势像屋脊的类型称为屋脊型边缘，c是a反方向情况，b,d是阶跃型边缘。

边缘的检测可以通过一阶导数、二阶导数计算，我们以a,b图为例(c,d类似)，其一阶导数，二阶导数图如下

1474354168223.jpg

在实际应用中，一般只考虑阶跃边缘，因为只要采样足够或者说窗口足够小，屋脊型边缘也可以看做是阶跃边缘。

对于阶跃边缘可以使用一阶导数的极值来判断边缘。 梯度算子定义是：

为了简化计算，一般将梯度算子写成

在图像中，导数运算离散成差分运算，于是得到下面一些一阶算子

罗伯特算子

对应卷积模板为

1474354921637.jpg

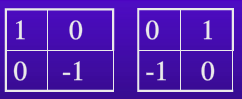
可见该算子对对角边缘检测效果较好。

Sobel算子

对应的卷积模板为

1474355261670.jpg

该算子其实是经过了高斯平滑后计算差分。

Prewitt算子(方向模板)

对应的卷积模板为

1474355378621.jpg

即不同方向的一阶导数。

对于阶跃边缘还可以使用二阶导数的过零点(zero-acrossing)判定

Laplace算子就是二阶导数算子，其定义为两个方向上一阶导数的内积。

我们用表示Laplace算子,则二维的laplace算子为

对于图像使用二阶差分代替二阶导数，则

于是二阶laplace算子的卷积模板可以为

如果我们考虑到四个方向，即

则卷积模板为

计算出每一像素点的二阶导数值之后，我们希望找到过零点，但图像是离散的，要找过零点还需进行拟合，拟合后的曲线找到过零点还要在离散过程很麻烦且完全没必要。这里可以直接寻找二阶导数正负交替的点作为边缘点。

二维图像的例子

1474357107462.jpg

对于阶跃边缘，梯度算子检测的范围较广，如下图中绿色线波峰很宽域内值都近似，而laplace算子(蓝色线)计算的是过零点，显然精确很多，下图中红色线是阶跃信号。

1474357684604.jpg

但是laplace算子是一种高通滤波模型，对于出现的独立噪声非常敏感，所以一般先对图像进行平滑之后再使用laplace算子检测边缘，使用Gaussian平滑和Laplace算子就形成了LoG算子。

高斯拉普拉斯算子(LoG,Laplacian of Gaussian)

假设对图像,使用尺度为的高斯平滑

然后再使用Laplace算子检测边缘

其中*是卷积符号，这是因为

定义高斯拉普拉斯算子

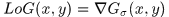
相当于对高斯模板先进行Laplace再与图像进行平滑。

将LoG展开，看其具体形式

所以

即高斯平滑后乘以与位置有关的系数。

一维情形下高斯函数及其一阶导数，和LoG的曲线图

1474362270473.jpg

LoG模板可以为

高斯差分算子(DoG,Difference of Gaussian)

类似于高斯拉普拉斯算子，DoG同样首先对图像进行高斯平滑。

定义DoG算子：

则高斯平滑后差分图像为

为什么DoG可以检测边缘，具体理论我们稍后再分析，这里先给出一个直观感受

1474363017387.jpg

我们发现这里DoG算子曲线和上文中的LoG算子曲线非常相似，因此它可以作为LoG的近似来检测边缘。

未完待续，下面我们将分析尺度不变的LoG，以及DoG和LoG的关系。

参考文献：

1. Blob detection https://en.wikipedia.org/wiki/Blob_detection#The_determinant_of_the_Hessian

2. 边缘检测 http://fourier.eng.hmc.edu/e161/lectures/gradient/node6.html

3. Laplace Operator http://fourier.eng.hmc.edu/e161/lectures/gradient/node7.html

4. Laplacian of Gaussian http://fourier.eng.hmc.edu/e161/lectures/gradient/node8.html

5. Difference of Gaussian http://fourier.eng.hmc.edu/e161/lectures/gradient/node9.html

6. LoG http://homepages.inf.ed.ac.uk/rbf/HIPR2/log.htm