*POJ 1222 高斯消元

EXTENDED LIGHTS OUT

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 9612		Accepted: 6246

Description

In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right.


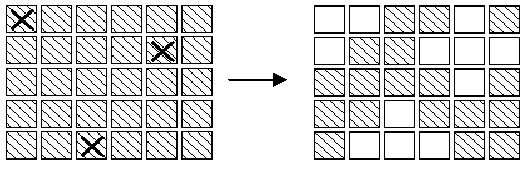
The aim of the game is, starting from any initial set of lights on
in the display, to press buttons to get the display to a state where all
lights are off. When adjacent buttons are pressed, the action of one
button can undo the effect of another. For instance, in the display
below, pressing buttons marked X in the left display results in the
right display.Note that the buttons in row 2 column 3 and row 2 column 5
both change the state of the button in row 2 column 4,so that, in the
end, its state is unchanged.



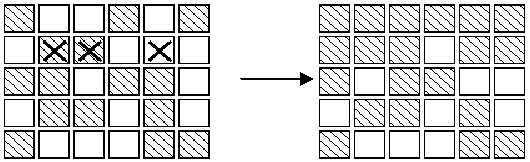
Note:

1. It does not matter what order the buttons are pressed.

2. If a button is pressed a second time, it exactly cancels the
effect of the first press, so no button ever need be pressed more than
once.

3. As illustrated in the second diagram, all the lights in the first
row may be turned off, by pressing the corresponding buttons in the
second row. By repeating this process in each row, all the lights in the
first

four rows may be turned out. Similarly, by pressing buttons in
columns 2, 3 ?, all lights in the first 5 columns may be turned off.

Write a program to solve the puzzle.

Input

The
first line of the input is a positive integer n which is the number of
puzzles that follow. Each puzzle will be five lines, each of which has
six 0 or 1 separated by one or more spaces. A 0 indicates that the light
is off, while a 1 indicates that the light is on initially.

Output

For
each puzzle, the output consists of a line with the string: "PUZZLE
#m", where m is the index of the puzzle in the input file. Following
that line, is a puzzle-like display (in the same format as the input) .
In this case, 1's indicate buttons that must be pressed to solve the
puzzle, while 0 indicate buttons, which are not pressed. There should be
exactly one space between each 0 or 1 in the output puzzle-like
display.

Sample Input

2
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0
0 0 1 0 1 0
1 0 1 0 1 1
0 0 1 0 1 1
1 0 1 1 0 0
0 1 0 1 0 0

Sample Output

PUZZLE #1
1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0
PUZZLE #2
1 0 0 1 1 1
1 1 0 0 0 0
0 0 0 1 0 0
1 1 0 1 0 1
1 0 1 1 0 1

Source

Greater New York 2002

题意：

有5行6列共30个开关，每按动一个开关，该开关及其上下左右共5个开关的状态都会改变，初始给你这30个开关的状态求按动那些开关能够使这些开关的状态都是0.

思路：因为每盏灯，如果操作两次就相当于没有操作，所以相当于(操作次数)%2，即异或操作。

考虑一个2*3的图，最后需要的状态是 ：，如果初始状态为：。对这两个矩阵的每个数字做异或操作可以得到线性方程组每个方程的答案。

总共6盏灯，0-5。那么可以列出6个方程。

对于第0盏灯，会影响到它的是第0, 1, 3盏灯，因此可以列出方程1*x0 + 1*x1 + 0*x2 + 1*x3 + 0*x4 + 0*x5= 0。

对于第1盏灯，会影响到它的是第0, 1, 2,4盏灯，因此可以列出方程1*x0 + 1*x1 + 1*x2 + 0*x3 + 1*x4 + 0*x5 = 1。

对于第2盏灯，会影响到它的是第1, 2, 5盏灯，因此可以列出方程0*x0 + 1*x1 + 1*x2 + 0*x3 + 0*x4 + 1*x5 = 0。

.....

所以最后可以列出增广矩阵：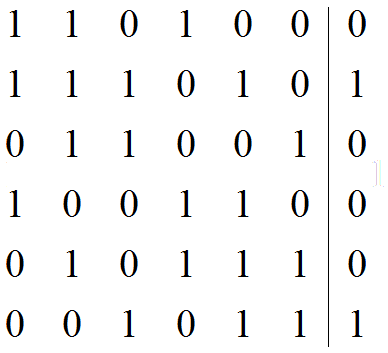

然后用高斯消元求这个矩阵的解就可以了。

30个变量30个方程组

代码：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 using namespace std;
 const int MAX=;
 int a[MAX][MAX]; //增广矩阵
 int x[MAX];  //解集
 int equ,var;  //行数和列数
 void init()
 {
     equ=;var=;
     memset(a,,sizeof(a));
     for(int i=;i<;i++)      //t点和上下左右都改变
         for(int j=;j<;j++)
         {
             int t=*i+j;
             a[t][t]=;
             if(i>) a[*(i-)+j][t]=;
             if(i<) a[*(i+)+j][t]=;
             if(j>) a[t-][t]=;
             if(j<) a[t+][t]=;
         }
 }
 void gaos()
 {
     int maxr;
     for(int k=,col=;k<equ&&col<var;k++,col++)
     {
         maxr=k;                      /****变为行阶梯形矩阵***/
         for(int i=k+;i<equ;i++)
             if(abs(a[i][col])>abs(a[maxr][col]))
             maxr=i;
         if(maxr!=k)
         {
             for(int i=col;i<var+;i++)
                 swap(a[maxr][i],a[k][i]);
         }
         if(a[k][col]==)  //第k行后的第col列全部是0了，换下一列
         {
             k--;
             continue;
         }
         for(int i=k+;i<equ;i++)   //第k行减去第i行的值赋给第i行，变为行阶梯型矩阵，由于都是01型矩阵，不用找lcm直接减就行
         {
             if(a[i][col]!=)
             {
                 for(int j=col;j<var+;j++)
                     a[i][j]^=a[k][j];
             }
         }
         for(int i=var-;i>=;i--)   //算出解集
         {
             x[i]=a[i][var];
             for(int j=i+;j<var;j++) //该行第var列是1说明该行有且只有一个x取1，若为0说明没有取1的x.
                 x[i]^=(a[i][j]&x[j]);
         }
     }
 }
 int main()
 {
     int t,ca=;
     scanf("%d",&t);
     while(t--)
     {
         ca++;
         init();
         for(int i=;i<;i++)
             scanf("%d",&a[i][]);
         gaos();
         printf("PUZZLE #%d",ca);
         for(int i=;i<;i++)
         {
             if(i%==) printf("\n%d",x[i]);
             else printf(" %d",x[i]);
         }
         printf("\n");
     }
     return ;
 }