三维空间中xoy平面上特定抛物线的正等测投影解析解的一种求法

背景

背景：为锻炼代同学，老师给了她一个反向工程微信“跳一跳”小游戏的任务，希望做一个一样的出来。跳一跳中，有方块，有小人，小人站在方块上。

这个游戏的玩法是，用手指按住手机屏幕，松开手指小人飞出。随着屏幕按压时间的增加，跳跃距离也会增加。希望得到小人跳跃的曲线。

观察到游戏中的抛物线并不对称，猜测它是在三维空间建模投影到一个平面上的。看《交互式计算机图形学》（Edward Angel，交互式计算机图形学，电子工业出版社，2012.5，p141）中，正等测（正等测等价于等轴测）的例子（图一）和跳一跳游戏中方块（图二）很相似（感谢代同学提供图片），猜测它使用的是三维空间正等测投影到二维平面上的投影。假设跳一跳的方块是由三维直角坐标系下的方块做正等测投影得到的，观察跳一跳方块中朝向我们的角，三个角都是120度，这和正等测的定义相符合。
图一
图二

解析解是什么

此前我的文章中讲了数值解的求法，按顺序给出了几百个点作为抛物线的采样，但有了解析式（参数方程也是一种解析式），就可以通过在公式中代入参数来求得坐标，而且可以求得精确的坐标（数值解并不精确）。比如，y=x^2精确的描述了一条抛物线。

一段题外话

与张慧杰老师讨论了计算机图形学opengl库的本质。都是矢量图形，用矩阵运算可以实现各种变换，光栅化后得到点。屏幕是一个一个的像素点，矢量图形要变成像素点才能显示在屏幕上。

矩阵与坐标变换

在计算机图形学中，三维的点用四维齐次坐标表示。点的投影，可以通过点左乘一个变换矩阵来实现。正等测的变换矩阵是：

将抛物线y=x^2表示为参数方程形式。
x=t
y=t^2
z=0
观察该参数方程知，该抛物线可看作齐次坐标下点（t，t^2，0，1），其中t为实数。
点乘以变换矩阵，得到变换后的点。
结果为：
x = 0.7071 t - 0.7071 t^2
y = 0
z = -0.4082 t - 0.4082 t^2
于是
x = 0.7071 t - 0.7071 t^2
y = 0
z = -0.4082 t - 0.4082 t^2
就是三维空间中抛物线y=x^2正等测投影后的抛物线参数方程。
在跳一跳游戏的三维空间中，如图1….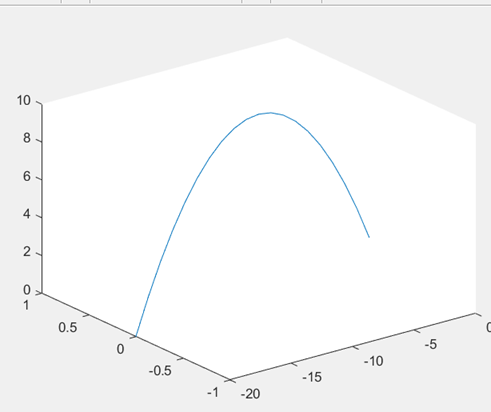
所示的抛物线的隐函数表达式是z=(100-(x-10)(x-10))/10（0<x<=20）
这条抛物线的参数方程为
x=-i
z=(100-(i-10)(i-10))/10（0<i<=20）
正等测变换过程就是矩阵乘法，将（x，y，z，i）左乘正等测投影矩阵，得到变换后的参数方程。
变换后的参数方程为
x=0.7071t
y=-0.4082t+0.8165(100-(t-10)(t-10))/10 （0<t<=20）

正等测变换后的抛物线如图2所示

在研发中的应用

在跳一跳游戏中，代秋彤同学调用由代秋彤同学提供的函数，抛物线数组 foo(起始点坐标，x的系数)。采样数量事先约定为采样共八个点。x是平面中抛物线的二次项。
由起始点坐标、x的系数可以确定抛物线。
根据平移变换，把抛物线的起点平移到起始点坐标。根据伸缩变换，改变投影前的抛物线的x的系数，抛物线将被拉长。我们观察到，跳一跳小游戏中不管抛物线多长，其高度不变。于是我们只拉长/缩短抛物线，这样符合我们观察到的现象。

应用示例

如，根据如图3所示的抛物线，代秋彤同学传来起始坐标（62,221）和x的系数1/2
隐函数方程：
z(x)=100 - (x/2-10)*(x/2-10))/2

参数方程：
x=t
z=100 - (t/2-10)*(t/2-10))/2

正等测变换后的参数方程：
x = 0.7071t
z = -0.4082t + 0.8165(100 - (t/2-10)(t/2-10))/2

平移：
x = 0.7071t-14.1422
z = -0.4082t + 0.8165(100 - (t/2-10)(t/2-10))/2+8.1642

根据采样间隔得到采样点:
(65,221) (65,199) (69,187) (72,176) (77,172) (81,176) (86,187) (90,205)

根据采样点，我们可以用小人在屏幕上画出曲线。
感谢小霞给出写作意见。
感谢刘典老师，没有他我们还在错误的路线上继续。
感谢代同学与我讨论、帮助我给出数据。