平衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree)又称AVL树

平衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree)又称AVL树

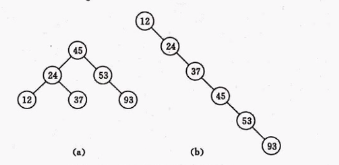
(a)和(b)都是排序二叉树，但是查找（b）的93节点就需要查找6次，查找（a）的93节点就需要查找3次，所以（b）的效率不高。

平衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree)又称AVL树。它或者是一颗空树，或者是具有下列性质的二叉树：它的左子树和右子树的深度只差的绝对值不超过1。若将二叉树上节点的平衡因子BF（Balance Factor)定义为该节点的左子树的深度减去它右子树的深度，则平衡二叉树上所有节点的平衡因子只可能是-1，0，1。只要二叉树上有一个节点的平衡因子的绝对值大于1，则该二叉树就是不平衡的。

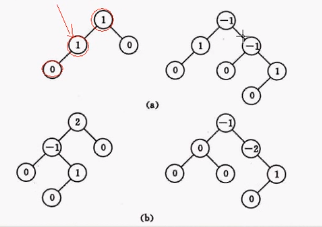
上图（a)是平衡二叉树，(b)不是平衡二叉树，因为有的节点的平衡因子大于1了。

插入节点的大致思路：

• 首先找到插入节点的位置，插入节点
• 插入节点后，调整相关节点的平衡因子
• 调整平衡因子后，如果发现树不平衡了，就要进行节点的调整（单左旋转，或单右旋转，或双旋转（先左后又，或者先右后左）。

avl_tree.h

#ifndef __AVLTREE__
#define __AVLTREE__

#include<stdio.h>
#include<malloc.h>
#include<assert.h>
#include "nodestack.h"

#define Type int
#define FALSE 0
#define TRUE 1
#define BOOL int

typedef struct AVLNode{
  Type data;
  struct AVLNode* left;
  struct AVLNode* right;
  int bf;//平衡因子
}AVLNode;

typedef struct AVLTree{
  struct AVLNode* root;
}AVLTree;

void init_avl_tree(AVLTree* avl);
//插入节点
BOOL insert_avl(AVLTree* avl, Type t);

#endif

avl_tree.c

#include "avl_tree.h"

void init_avl_tree(AVLTree* avl){
  avl->root = NULL;
}
AVLNode* malNode(Type x){
    AVLNode* t = (AVLNode*)malloc(sizeof(AVLNode));
    assert(NULL != t);
    t->data  = x;
    t->left  = NULL;
    t->right = NULL;
    t->bf    = 0;
    return t;
}
//右旋转
void rotateR(AVLNode** t){
  AVLNode* subR = *t;
  *t = (*t)->left;
  subR->left = (*t)->right;
  (*t)->right = subR;
  (*t)->bf = 0;
  subR->bf = 0;

}
//左旋转
void rotateL(AVLNode** t){
  AVLNode* subL = *t;
  *t = (*t)->right;
  subL->right = (*t)->left;
  (*t)->left = subL;
  (*t)->bf = 0;
  subL->bf = 0;

}
//左右旋转
void rotateLR(AVLNode** t){
  AVLNode* subR = *t;
  AVLNode* subL = subR->left;
  *t = subL->right;

  subL->right = (*t)->left;
  (*t)->left = subL;
  if((*t)->bf <= 0){///??
    subL->bf = 0;
  }
  else{
    subL->bf = -1;
  }

  subR->left = (*t)->right;
  (*t)->right = subR;
  if((*t)->bf == -1){
    subR->bf = 1;//???
  }
  else{
    subR->bf = 0;//???
  }

  (*t)->bf = 0;
}
//右左旋转
void rotateRL(AVLNode** t){
  AVLNode* subL = *t;
  AVLNode* subR = subL->right;
  *t = subR->left;

  subR->left = (*t)->right;
  (*t)->right = subR;
  if((*t)->bf >= 0){
    subR->bf = 0;
  }
  else{
    subR->bf = 1;
  }

  subL->right = (*t)->left;
  (*t)->left = subL;
  if((*t)->bf == 1){
    subL->bf = -1;
  }
  else{
    subL->bf = 0;
  }

  (*t)->bf = 0;
}
//插入树的节点
BOOL insert_avl_node(AVLNode** t, Type x){
  AVLNode* p = *t;
  AVLNode* parent = NULL;

  nodestack st;
  init(&st);

  while(p != NULL){
    if(x == p->data)
      return FALSE;
    parent = p;
    push(&st, parent);
    if(x < p->data)
      p = p->left;
    else
      p = p->right;
  }
  p = malNode(x);
  //插入节点为root节点
  if(parent == NULL){
    *t = p;
    return TRUE;
  }
  //插入节点不是root节点
  if(x < parent->data)
    parent->left = p;
  else
    parent->right = p;

  //调整BF
  while(length(&st) != 0){
    parent = getTop(&st);
    pop(&st);
    if(parent->left == p){
      parent->bf--;
    }
    else{
      parent->bf++;
    }

    if(parent->bf == 0){
      break;
    }
    if(parent->bf == 1 || parent->bf == -1){
      p = parent;
    }
    else{
      //旋转树，让树变成平衡树
      int flag = (parent->bf < 0) ? -1 : 1;
      //符号相同，说明是一条直线，不是折线，所以单旋转
      if(p->bf == flag){
	//因为是撇/，所以右旋转
	if(flag == -1){
	  rotateR(&parent);
	}
	//因为是捺\，所以左旋转
	else{
	  rotateL(&parent);
	}
      }
      //符号不同，说明是折线，所以双旋转
      else{
	//折线的角指向右>
	if(flag == 1){
	  rotateRL(&parent);
	}
	//折线的角指向左<
	else{
	  rotateLR(&parent);
	}
      }
      break;
    }
  }

  if(length(&st) == 0){
    *t = parent;
  }
  else{
    AVLNode* q = getTop(&st);
    if(q->data > parent->data){
      q->left = parent;
    }
    else{
      q->right = parent;
    }
  }

  clear(&st);
  return TRUE;
}
//插入节点
BOOL insert_avl(AVLTree* avl, Type t){
  return insert_avl_node(&avl->root, t);
}

avl_treemain.c

#include "avl_tree.h"

int main(){
  AVLTree avl;
  init_avl_tree(&avl);

  //Type ar[] = {13,24,37,90,53};
  //Type ar[] = {30,20,10};
  //Type ar[] = {30,20,40,10,25,5,22,28,21};
  //Type ar[] = {30,20,10};
  //Type ar[] = {50,40,60,10,45,70,5,30,20,12};
  Type ar[] = {30,20,50,10,40,70,60,80,55};

  int n = sizeof(ar) / sizeof(Type);
  for(int i = 0; i < n; ++i){
    insert_avl(&avl, ar[i]);
  }
  return 0;
}

完整代码

编译方法：g++ -g nodestack.c avl_tree.c avl_treemain.c