C++二分图匹配基础：zoj1002 FireNet 火力网

直接给出题目吧。。。

问题 D(1988): 【高级算法】火力网

时间限制: 1 Sec 内存限制: 128 MB

题目描述

给出一个N*N的网格，用'.'表示空地，用'X'表示墙。在网格上放碉堡，可以控制所在的行和列，但不能穿过墙。

问：最多能放多少个碉堡？

输入

第1行：一个整数N(N<=20)

接下来N行，每行N个字符

输出

第1行：1个整数，表示最多可放碉堡数。

样例输入

4

.X..

....

XX..

....

样例输出

5

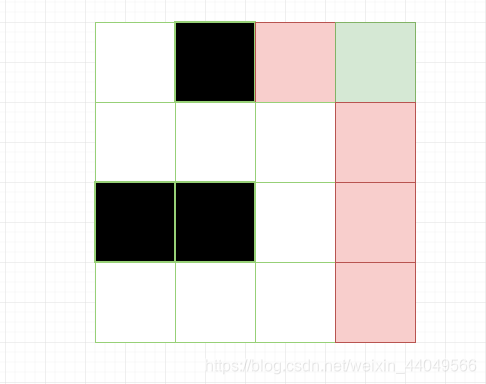
不知为何此题的图片居然莫名其妙的消失了，于是自己动手画了一张关于样例的图。



来解释一下样例吧。

现在我们要做的就是在白色格子上放上碉堡。每个碉堡都可以控制它所在的行和列，直到遇到了黑色格子。下图便是一个碉堡的攻击范围。



我们要做的便是在这个地图中放入尽量多的骑士，使他们都不能互相攻击。

题意应该说的很明显了吧，现在我们就要思考一下此题的做法。

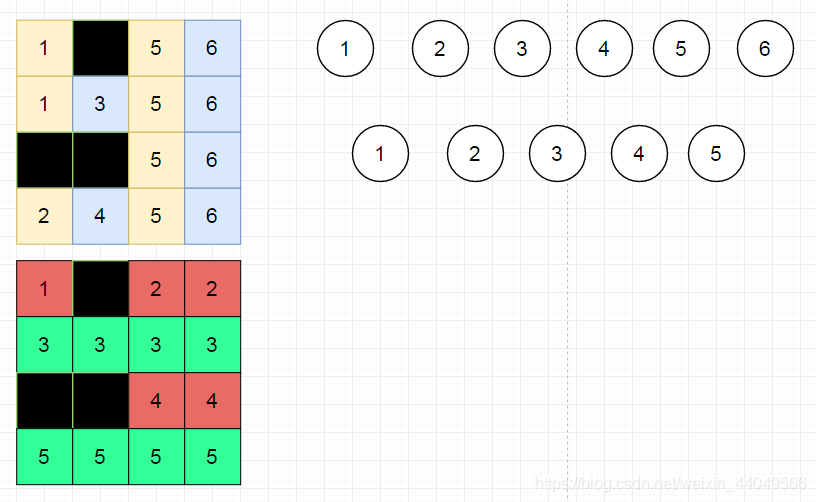
骑士的攻击有两个方向，到黑格子为止。所以我们不妨将所有的独立的横向块和独立的竖向块分为两个部，并给它们编上号。

我们可以发现如果任选两个相交的横块与竖块，在它们的交点上放上一个碉堡，则这两个块中都不能再放上碉堡了。这便符合二分图的性质。而最多的可放骑士数则是二分图的最大匹配。

于是我们的方法就出来了，将所有的横块与竖块编上号，如果它们相交便连上边。最后只需要求出最大匹配数即可。具体实现详见代码。

代码

#include <iostream>
#include <cstring>
#include <vector>
using namespace std;

#define N 50

char map[N][N];
int fuck[N][N],n,m,vis[N],match[N];
vector <int> G[N];

void Handle() {
    int cnt=1;
    for(int j=1;j<=n;j++) {
        int flag=0;
        for(int i=1;i<=n;i++) {
            if(map[i][j]!='X')
                fuck[i][j]=cnt,flag=0;
            else if(map[i-1][j]!='X')
                cnt++,flag=1;
        }
        cnt++;
    }

    m=cnt;cnt++;
    for(int i=1;i<=n;i++) {
        for(int j=1;j<=n;j++) {
            if(map[i][j]!='X')
                G[fuck[i][j]].push_back(cnt);
            else if(map[i][j-1]!='X')
                cnt++;
        }
        cnt++;
    }

}

bool dfs(int u) {
    for(int i=0,v;i<G[u].size();i++) {
        v=G[u][i];
        if(vis[v]) continue;
        vis[v]=1;
        if( !match[v] || dfs( match[v] )) {
            match[v]=u;
            return 1;
        }
    }
    return 0;
}

int hungary() {
    int ans=0;
    for(int i=1;i<=m;i++) {
        memset(vis,0,sizeof(vis));
        if(dfs(i)) ans++;
    }
    return ans;
}

int main() {
    cin>>n;
    for(int i=1;i<=n;i++ ) for(int j=1;j<=n;j++)
        cin>>map[i][j];
    Handle();
    /*for(int i=1;i<=m;i++) {
        for(int j=0;j<G[i].size();j++)
            cout<<G[i][j]<<' ';
        cout<<endl;
    } */

    cout<<hungary();
}

最后说一句。有个奇怪的想法，如果这个地图是三维的，是不是就需要用到“三分图最大匹配”了？