SGD训练时收敛速度的变化研究。

一个典型的SGD过程中，一个epoch内的一批样本的平均梯度与梯度方差，在下图中得到了展示。

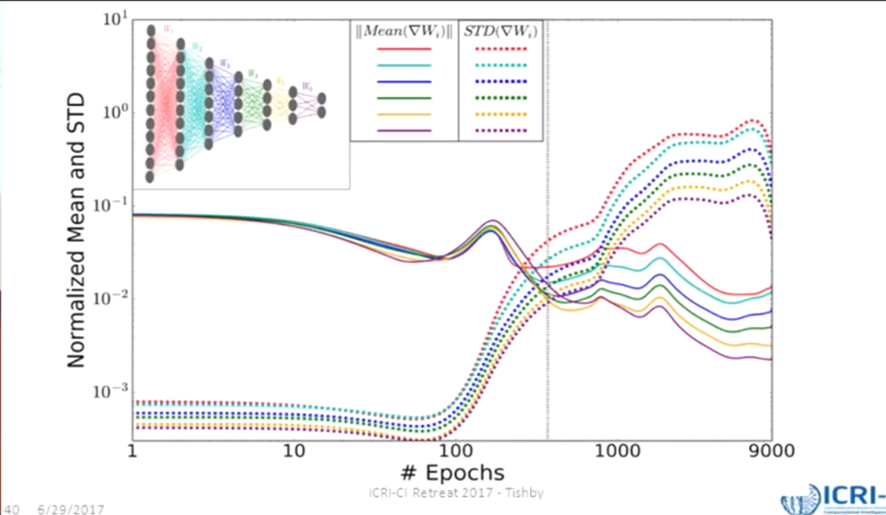
无论什么样的网络结构，无论是哪一层网络的梯度，大体上都遵循下面这样的规律：

高信号/噪音比一段时间之后，信号/噪音比逐渐降低，收敛速度减缓，梯度的方差增大，梯度均值减小。

噪音增加的作用及其必要性会在另一篇文章中阐述，这里仅讨论噪音的产生对于模型收敛速度能够产生怎样的影响。

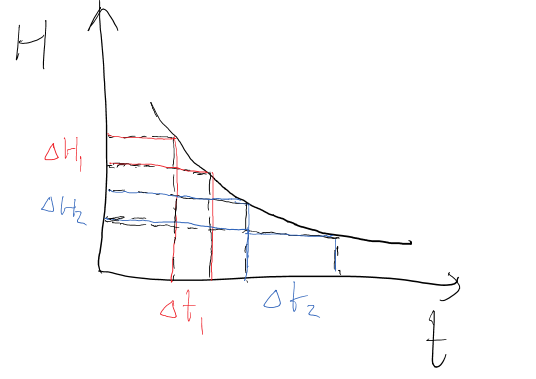
首先定义模型收敛速度：训练后期，噪音梯度导致权重更新时，导致系统新增的熵 H（混乱度）对于SGD迭代次数 t 的导数。

对于第k层的权重的梯度，每一轮（时间t）更新：

\[\frac{\partial {{\mathbf{W}}^{\left( k \right)}}}{\partial t}=-\nabla \operatorname{E}({{\mathbf{W}}^{\left( k \right)}})+\beta _{\left( k \right)}^{-1}\xi \left( t \right)\]

其中E是全局损失函数， $\beta $是信号/噪音比，$\xi $是高斯白噪音， $P\left( \xi \left( t \right) \right)=Norm\left( 0,\sigma \left( t \right) \right)$ ，方差$\sigma \left( t \right)$随着时间增加而变大。

因为使用高噪音进行梯度下降更新权重W时引进了额外的熵，考虑熵的变化$\Delta H({{\mathbf{W}}^{(k)}})$

假设将损失函数E分割成非常多个小区间，问题转化为：$\Delta H({{\mathbf{W}}^{(k)}})\text{=}\Delta H({{\text{E}}_{1}}({{\mathbf{W}}^{(k)}}),{{\text{E}}_{2}}({{\mathbf{W}}^{(k)}})......{{\text{E}}_{N}}({{\mathbf{W}}^{(k)}}))$

已知$\operatorname{H}\left( E \right)=-\underset{\text{i}}{\mathop{\sum }}\,p\left( {{\text{E}}_{\text{i}}} \right)\log p\left( {{\text{E}}_{\text{i}}} \right)$

\[\frac{\partial \operatorname{H}}{\partial p}=-\left( \sum\limits_{\text{i}}{\log \left( p\left( {{E}_{i}} \right) \right)+1} \right)\]

又已知系统达到热平衡后，使熵最大的p(W)分布是玻尔兹曼分布（参见Boltzmann与最大熵的关联文章）

${{p}_{E={{E}_{i}}}}\left( \mathbf{W} \right)=\frac{1}{\text{Z}}{{\text{e}}^{-\beta {{E}_{i}}\left( \mathbf{W} \right)}}$ ，Z是配分函数partition function $Z=\sum\limits_{E'}{{{e}^{-\beta E'(\mathbf{W})}}}$

考虑热平衡附近时，p怎样随着E改变：

\[\frac{\partial p}{\partial E}=\frac{\partial }{\partial {{E}_{\text{i}}}}\left( {{{e}^{-\beta {{E}_{i}}}}}/{\left( {{e}^{-\beta {{E}_{i}}}}+\sum\nolimits_{k\ne i}{{{e}^{-\beta {{E}_{k}}}}} \right)}\; \right)=-\beta p(1-p)\]

使用链式法则得到：

$\frac{\partial \text{H}}{\partial t}=\sum\limits_{i}{\frac{\partial \text{H}}{\partial {{p}_{i}}}\frac{\partial {{p}_{i}}}{\partial {{\text{E}}_{i}}}\frac{\partial {{\text{E}}_{i}}}{\partial \mathbf{W}}\frac{\partial \mathbf{W}}{\partial t}}$

训练到接近收敛时，尽管每次更新权重时计算的loss的白噪音会越来越大，但全局loss E会稳定得多，并且逐渐下降到一个比较小的区间内，所以只考虑该区间内对应的$\Delta \text{H}$以及$\Delta \text{t}$，带入前面求出的偏导得到：

\[\frac{\partial H}{\partial t}=\sum\limits_{\text{i}}{\left( \log \left( {{p}_{\text{i}}} \right)+1 \right)\beta {{p}_{i}}(1-{{p}_{i}})\nabla {{E}_{i}}(\mathbf{W})(-\nabla {{E}_{i}}(\mathbf{W})+\beta _{(k)}^{-1}\xi (t))}\]

噪音项在求期望时被平均成0，同时使用泰勒级数在p=1附近展开ln(p) ：$\ln (p)=(p-1)-\frac{1}{2}{{(p-1)}^{2}}+\frac{1}{3}{{(p-1)}^{3}}-......$

可推出

$(\log (p)+1)(1-p)=-p\log p+1-p+\log p\approx -p\log p+1-p+(p-1)-\frac{1}{2}{{(p-1)}^{2}}=-p\log p-\frac{1}{2}{{(p-1)}^{2}}$

当p_i接近1时，忽略二次项，得到熵H，既 -plogp

继续带入可得（注意beta后面是预期值符号，不是损失函数E）

\[\frac{\partial H}{\partial t}\approx \beta \sum\limits_{\text{i}}{-{{p}_{i}}{{\left( \nabla {{E}_{i}}(\mathbf{W}) \right)}^{2}}}H=-\beta \operatorname{E}\left[ {{\left( \nabla E(\mathbf{W}) \right)}^{2}} \right]H\]

这里看出当训练时在全局loss逐渐收敛到一个小区间E_i内，p_i趋近于1，这时候熵的该变量与训练迭代次数满足上述微分方程。

解微分方程得到：

$H=H_{0}\exp\left(-\beta\mathbb{E}\left[(\nabla E(W))^{2}\right])t\right)$

该方程只在全局loss相对稳定之后成立，此时SGD噪音带来的熵随训练时间的增加而指数减少。

半衰期之前一直被当做常量来看待，但其实半衰期随着全局梯度平方的预期值的减小，会逐渐增大。

也就是说要从噪音里引入固定量的熵，所消耗的时间（迭代轮数）会越来越多，甚至比普通的指数衰减花费更多的时间。

第k层权重更新噪音引入的熵 会以 给定下一层特征层时输入数据X的熵 的形式展现。

\[\Delta H(\delta {{\mathbf{W}}^{(k)}})=\Delta H(X|{{T}^{(k+1)}})\]

噪音引入的熵的作用，会在下面几篇介绍信息瓶颈理论的文章里详细阐述。