P2047 [NOI2007]社交网络（洛谷）

题目描述

在社交网络 ( Social Network ) 的研究中，我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题:
在一个社交圈子里有 nn 个人，人与人之间有不同程度的关系。我们将这个关系网络对应到一个 nn 个结点的无向图上，两个不同的人若互相认识，则在他们对应的结点之间连接一条无向边，并附上一个正数权值 cc ，cc 越小，表示两个人之间的关系越密切。我们可以用对应结点之间的最短路长度来衡量两个人 ss 和 tt 之间的关系密切程度，注意到最短路径上的其他结点为 ss 和 tt 的联系提供了某种便利，即这些结点对于 ss 和 tt 之间的联系有一定的重要程度。我们可以通过统计经过一个结点 vv 的最短路径的数目来衡量该结点在社交网络中的重要程度。考虑到两个结点 AA 和 BB 之间可能会有多条最短路径。我们修改重要程度的定义如下：令 C_{s,t}Cs,t 表示从s到t的不同的最短路的数目，C_{s,t}(v)Cs,t(v) 表示经过 vv 从 ss 到 tt 的最短路的数目；则定义：

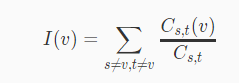
为结点 vv 在社交网络中的重要程度。为了使 I(v)I(v) 和 C_{s,t}(v)Cs,t(v) 有意义，我们规定需要处理的社交网络都是连通的无向图，即任意两个结点之间都有一条有限长度的最短路径。现在给出这样一幅描述社交网络的加权无向图，请你求出每一个结点的重要程度。

输入输出格式

输入格式：

输入第一行有两个整数 nn 和 mm ，表示社交网络中结点和无向边的数目。

在无向图中，我们将所有结点从 11 到 nn 进行编号。

接下来 mm 行，每行用三个整数 a , b , ca,b,c 描述一条连接结点 aa 和 bb ，权值为 cc 的无向边。注意任意两个结点之间最多有一条无向边相连，无向图中也不会出现自环（即不存在一条无向边的两个端点是相同的结点）。

输出格式：

输出包括 nn 行，每行一个实数，精确到小数点后 33 位。第 ii 行的实数表示结点 ii 在社交网络中的重要程度。

输入输出样例

输入样例#1：复制

输出样例#1：复制

说明

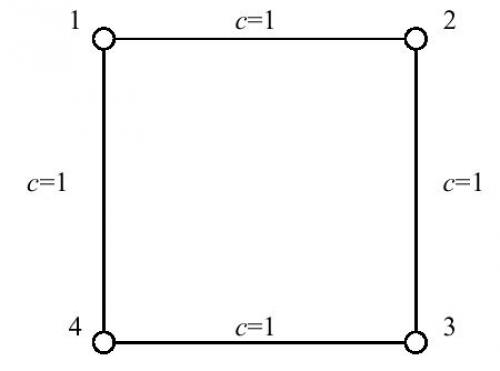
对于1号结点而言，只有2号到4号结点和4号到2号结点的最短路经过1号结点，而2号结点和4号结点之间的最短路又有2条。因而根据定义，1号结点的重要程度计算为1/2+1/2=1。由于图的对称性，其他三个结点的重要程度也都是1。

对于 50\%50% 的数据， n \le 10 , m \le 45n≤10,m≤45。
对于 100\%100% 的数据， n \le 100 , m \le 4500n≤100,m≤4500 ，任意一条边的权值 cc 是正整数且 1 \leqslant c \leqslant 10001⩽c⩽1000 。
所有数据中保证给出的无向图连通，且任意两个结点之间的最短路径数目不超过 10^{10}1010。

解析：

a:是图的邻接矩阵，d是图中任意两点直接的最短距离、c记录两点间最短路径的数目，f[v]记录经过v点的重要程度。


floyd算法: 
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
利用floyd算法求两点间最短路径的数目

 if(d[i][j]>d[i][k]+d[k][j]){

                    d[i][j]=d[i][k]+d[k][j];

                    c[i][j]=c[i][k]*c[k][j];

                }

 else if(d[i][j]==d[i][k]+d[k][j]){

                    c[i][j]+=c[i][k]*c[k][j];

                }

floyd后，再求每个点的重要程度：

 if(c[i][j]&&d[i][j]==d[i][k]+d[k][j])

                    f[k]+=double(c[i][k]*c[k][j])/c[i][j];

#include<iostream>

#include<cstring>

#include<cstdio>

using namespace std;

int n,m;

const int maxn=;

long long a[maxn][maxn],d[maxn][maxn],c[maxn][maxn];//注意数据类型

double f[maxn];

void floy(){

    for(int i=;i<=n;i++)

        for(int j=;j<=n;j++) d[i][j]=a[i][j];

    for(int k=;k<=n;k++)

        for(int i=;i<=n;i++)

            for(int j=;j<=n;j++)

                if(d[i][j]>d[i][k]+d[k][j]){

                    d[i][j]=d[i][k]+d[k][j];

                    c[i][j]=c[i][k]*c[k][j];

                }

                else if(d[i][j]==d[i][k]+d[k][j]){

                    c[i][j]+=c[i][k]*c[k][j];

                }

    for(int k=;k<=n;k++)

        for(int i=;i<=n;i++)

            for(int j=;j<=n;j++)

                if(c[i][j]&&d[i][j]==d[i][k]+d[k][j])

                    f[k]+=double(c[i][k]*c[k][j])/c[i][j];

}

int main(){

    cin>>n>>m;

    memset(a,0x3f,sizeof(a));

    for(int i=;i<=n;i++) a[i][i]=;

    for(int i=;i<=m;i++){

        int x,y,w;

        cin>>x>>y>>w;

        a[x][y]=a[y][x]=w;

        c[x][y]=c[y][x]=;

    }

    floy();

    for(int i=;i<=n;i++)

        printf("%.3lf\n",f[i]);

    return ;

}