2019-2020 ICPC, NERC, Southern and Volga Russian Regional Contest

目录

• Contest Info
• Solutions
  • A. Berstagram
  • C. Trip to Saint Petersburg
  • E. The Coronation
  • F. Data Center
  • G. Discarding Game
  • H. Happy Birthday
  • J. The Parade
  • L. Divide The Students
  • M. SmartGarden
  • N. Wires

Contest Info

---

[Practice Link](https://codeforces.com/contest/1250)

Solved	A	B	C	D	E	F	G	H	I	J	K	L	M	N
9/14	O	O	O	-	O	O	-	O	-	O	-	O	-	O

• O 在比赛中通过
• Ø 赛后通过
• ! 尝试了但是失败了
• - 没有尝试

Solutions

---

A. Berstagram

题意：

给出\(n\)个数，刚开始第\(i\)个数在第\(i\)个位置，有\(m\)次操作，将标号为\(a_i\)的数和它前面那个数交换位置，如果它已经在最前面了，那么不操作。

最后输出\(n\)行，表示每个数所待过的位置的下标的最小值和最大值

思路：

每次交换只会影响两个数，暴力即可。

代码：

view code

```c++
#include
using namespace std;
using pII = pair;
#define fi first
#define se second
const int N = 4e5 + 10;
int n, m, a[N], fa[N], b[N];
pII res[N];
void up(int x, int y) {
res[x].fi = min(res[x].fi, y);
res[x].se = max(res[x].se, y);
}

int main() {

while (scanf("%d%d", &n, &m) != EOF) {

for (int i = 1; i <= n; ++i) a[i] = i, fa[i] = i, res[i] = pII(i, i);

for (int i = 1; i <= m; ++i) scanf("%d", b + i);

for (int i = 1; i <= m; ++i) {

int x = b[i];

if (fa[x] == 1) continue;

int pre = a[fa[x] - 1];

swap(fa[x], fa[pre]);

swap(a[fa[x]], a[fa[pre]]);

up(x, fa[x]);

up(pre, fa[pre]);

// for (int j = 1; j <= n; ++j)

// printf("%d%c", a[j], " \n"[j == n]);

}

for (int i = 1; i <= n; ++i)

printf("%d %d\n", res[i].fi, res[i].se);

}

return 0;

}

</details>

### B. The Feast and the Bus

题意：
有$n$个人，$k$个小组，每个人属于一个小组，每个小组至少有一个人。
现在要租$r$辆巴士，每辆巴士的容量都为$s$，但是$s$和$r$可以自己定，使得能够装下所有人，并且满足以下两个限制条件：
- 同一组的人在同一辆巴士
- 一辆巴士最多有两个小组的人

使得$r \cdot s$最小

思路：
考虑$k$很小，我们可以枚举$r$，然后可以算出有多少辆巴士必须要两个小组，然后贪心放，让小组人数多的占用单组巴士，小组人数少的贪心配对，即最大的配最小的，次大的配次小的$\cdots$
时间复杂度$O(k^2)$

代码：
<details>
<summary>view code</summary>

```c++
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
int n, k, a[N];
ll gao(int x) {
	ll s = 0;
	int need = k - (2 * x - k);
	for (int i = 1, j = need; i < j; ++i, --j) {
		s = max(s, 1ll * a[i] + a[j]);
	}
	for (int i = need + 1; i <= k; ++i)
		s = max(s, 1ll * a[i]);
	return s;
}

int main() {
	while (scanf("%d%d", &n, &k) != EOF) {
		memset(a, 0, sizeof a);
		for (int i = 1, x; i <= n; ++i) {
			scanf("%d", &x);
			++a[x];
		}
		sort(a + 1, a + 1 + k);
		ll res = 1e18;
		for (int i = (k + 1) / 2; i <= k; ++i) {
			res = min(res, 1ll * i * gao(i));
		}
		printf("%lld\n", res);
	}
	return 0;
}

C. Trip to Saint Petersburg

题意：

给出\(n\)个工作，和一个参数\(k\)。

每个工作的工作时间为\([l_i, r_i]\)，可以获得\(p_i\)的利润，并且工作随便选，工作时间可以重叠。

唯一的代价就是所选择的工作中的最小的\(L = l_i\)，最大的\(R = r_i\)，代价就是\(k \cdot (R - L + 1)\)。

问所能获得的最大利润。

思路：

枚举右端点\(R\)，然后线段树维护左端点的贡献，每次要将\(r_i = R\)的工作的贡献加给左端点在\([1, l_i]\)范围内的。

然后查询区间最值即可。

代码：

view code

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pIL = pair<int, ll>;
#define fi first
#define se second
const int N = 2e5 + 10;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int n, m, pl[N], pr[N]; ll k;
vector <vector<pIL>> vec;

struct SEG {
	struct node {
		ll Max, lazy; int pos;
		node() { Max = -INF; lazy = pos = 0; }
		void up(ll x) {
			Max += x;
			lazy += x;
		}
		node operator + (const node &other) const {
			node res = node();
			if (Max >= other.Max) {
				res.Max = Max;
				res.pos = pos;
			} else {
				res.Max = other.Max;
				res.pos = other.pos;
			}
			return res;
		}
	}t[N << 2], res;
	void build(int id, int l, int r) {
		t[id] = node();
		if (l == r) {
			t[id].Max = 0;
			t[id].pos = l;
			return;
		}
		int mid = (l + r) >> 1;
		build(id << 1, l, mid);
		build(id << 1 | 1, mid + 1, r);
		t[id] = t[id << 1] + t[id << 1 | 1];
	}
	void down(int id) {
		ll &lazy = t[id].lazy;
		if (lazy) {
			t[id << 1].up(lazy);
			t[id << 1 | 1].up(lazy);
			lazy = 0;
		}
	}
	void update(int id, int l, int r, int ql, int qr, ll v) {
		if (l >= ql && r <= qr) {
			t[id].up(v);
			return;
		}
		int mid = (l + r) >> 1;
		down(id);
		if (ql <= mid) update(id << 1, l, mid, ql, qr, v);
		if (qr > mid) update(id << 1 | 1, mid + 1, r, ql, qr, v);
		t[id] = t[id << 1] + t[id << 1 | 1];
	}
	void query(int id, int l, int r, int ql, int qr) {
		if (l >= ql && r <= qr) {
			res = res + t[id];
			return;
		}
		int mid = (l + r) >> 1;
		down(id);
		if (ql <= mid) query(id << 1, l, mid, ql, qr);
		if (qr > mid) query(id << 1 | 1, mid + 1, r, ql, qr);
	}
}seg;

int main() {
	while (scanf("%d%lld", &n, &k) != EOF) {
		vec.clear(); vec.resize(N);
		m = 2e5;
		for (int i = 1; i <= n; ++i) {
			int l, r; ll p;
			scanf("%d%d%lld", &l, &r, &p);
			pl[i] = l, pr[i] = r;
			vec[r].push_back(pIL(l, p));
		}
		ll p = 0; int L = -1, R = -1;
		seg.build(1, 1, m);
		for (int i = 1; i <= m; ++i) {
			seg.update(1, 1, m, 1, i, -k);
			for (auto &it : vec[i])
				seg.update(1, 1, m, 1, it.fi, it.se);
			seg.res = SEG::node();
			seg.query(1, 1, m, 1, i);
			if (seg.res.Max > p) {
				p = seg.res.Max;
				L = seg.res.pos;
				R = i;
			}
		}
		if (p == 0) puts("0");
		else {
			vector <int> vec;
			for (int i = 1; i <= n; ++i)
				if (pl[i] >= L && pr[i] <= R)
					vec.push_back(i);
			int sze = vec.size();
			printf("%lld %d %d %d\n", p, L, R, sze);
			for (int i = 0; i < sze; ++i)
				printf("%d%c", vec[i], " \n"[i == sze - 1]);
		}
	}
	return 0;
}

E. The Coronation

题意：

给出\(n\)个\(01\)串，每个\(01\)串可以\(reverse\)，求最少的\(reverse\)次数，使得任意两个串的有大于等于\(k\)个位置的字符是相同的。

代码：

view code

#include <bits/stdc++.h>

using namespace std;

const int N = 60;

struct Edge {
	int v, p;//1 same

	Edge() {}

	Edge(int v, int p): v(v), p(p) {}
};

bool F;
int n, m, k;
string s[N];
vector<vector<Edge> > G;

bool ok(const string &S, const string &T) {
	int cnt = 0;
	for (int i = 0; i < m; ++i) {
		if (S[i] == T[i]) ++cnt;
	}
	return cnt >= k;
}

int col[N], vis[N];
vector<int> vec, res;

void DFS(int u) {
	if (!F) return ;
	vis[u] = 1;
	vec.push_back(u);
	for (auto &it: G[u]) {
		if (col[it.v] == -1) {
			if (it.p) {
				col[it.v] = col[u];
			} else {
				col[it.v] = col[u] ^ 1;
			}
			DFS(it.v);
		} else {
			if (it.p) {
				if (col[it.v] != col[u]) {
					F = false;
					break;
				}
			} else {
				if (col[it.v] != (col[u] ^ 1)) {
					F = false;
					break;
				}
			}
		}
	}
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	int T;
	cin >> T;
	while (T--) {
		cin >> n >> m >> k;
		G.clear();
		G.resize(n + 1);
		memset(vis, 0, sizeof vis);
		memset(col, -1, sizeof col);
		for (int i = 1; i <= n; ++i) {
			cin >> s[i];
		}
		F = true;
		for (int i = 1; i <= n; ++i) {
			for (int j = i + 1; j <= n; ++j) {
				int cnt = 0;
				int same = 0;
				if (ok(s[i], s[j])) {
					cnt++;
					same = 1;
				}
				reverse(s[j].begin(), s[j].end());
				cnt += ok(s[i], s[j]);
				reverse(s[j].begin(), s[j].end());
				if (cnt == 0) {
					F = false;
					break;
				}
				if (cnt == 1) {
					G[i].push_back(Edge(j, same));
					G[j].push_back(Edge(i, same));
				}
			}
			if (!F) {
				F = false;
				break;
			}
		}
		if (!F) {
			cout << "-1\n";
			continue;
		}
		res.clear();
		for (int i = 1; i <= n; ++i) {
			if (!vis[i]) {
				col[i] = 1;
				vec.clear();
				DFS(i);
				int cnt[2] = {0, 0};
				for (auto &it: vec) {
					cnt[col[it]]++;
				}
				int now = 0;
				if (cnt[1] < cnt[0]) {
					now = 1;
				}
				for (auto &it : vec) {
					if (col[it] == now) {
						res.push_back(it);
					}
				}
			}
		}
		if (!F) {
			cout << "-1\n";
		} else {
			int sze = res.size();
			cout << sze << "\n";
			for (int i = 0; i < sze; ++i) {
				if (i) cout << " ";
				cout << res[i];
			}
			cout << "\n";
		}
	}
	return 0;
}

F. Data Center

题意：

给出一个矩形的面积\(n\)，求所有合法矩形中的最小周长。

思路：

暴力分解。

代码：

view code

#include <bits/stdc++.h>
using namespace std;

int main() {
	int n;
	while (scanf("%d", &n) != EOF) {
		int res = 1e9;
		for (int i = 1; i <= n; ++i) {
			if (n % i == 0) {
				res = min(res, i + n / i);
			}
		}
		res *= 2;
		printf("%d\n", res);
	}
	return 0;
}

G. Discarding Game

题意：

有两个人玩游戏，刚开始两个人的分数都是\(0\)，每一轮，\(A\)的分数会加上\(a_i\)，\(B\)的分数会加上\(b_i\)，如果某个人的分数大于等于\(k\)，它就输了，如果两个人都大于等于\(k\)，两个人都输了。

如果最后过完了\(n\)轮，两人的分数都小于\(k\)，那么是平局。

赢的情况是其中某个人输了，那么另一个人就赢了。

现在\(A\)有超能力，它可以在每一轮加分结束后按下一个按钮，假定此时\(A\)的分数为\(x\)，\(B\)的分数为\(y\), \(A\)的分数变成\(max(0, x - y)\)，\(B\)的分数变成\(max(0, y - x)\)。

现在求最少次数使得\(A\)赢了。

H. Happy Birthday

题意：

给出\([0, 9]\)每种数字的个数，问最小的不能被拼出来的数是多少。

代码：

view code

#include <bits/stdc++.h>

using namespace std;

int a[100];

int main() {
	int T;
	scanf("%d", &T);
	while (T--) {
		for (int i = 0; i < 10; ++i) scanf("%d", a + i);
		int Min = a[0] + 2;
		for (int i = 1; i < 10; ++i) Min = min(Min, a[i] + 1);
		if (Min == a[0] + 2) {
			printf("1");
			for (int i = 1; i <= a[0] + 1; ++i) printf("0");
			puts("");
		} else {
			for (int i = 1; i < 10; ++i) {
				if (Min == a[i] + 1) {
					for (int j = 1; j <= a[i] + 1; ++j) printf("%d", i);
					puts("");
					break;
				}
			}
		}
	}
	return 0;
}

J. The Parade

代码：

view code

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int N = 1e5 + 10;

int n;
ll k;
ll a[N], b[N];

bool check(ll x) {
	ll cnt = 0, remind = 0;
	for (int i = 1; i <= n; ++i) {
		b[i] = a[i];
		if (b[i] >= x - remind) {
			cnt++;
			b[i] -= x - remind;
			remind = 0;
		}
		cnt += b[i] / x;
		remind = b[i] % x;
		if (cnt >= k) return true;
	}
	return cnt >= k;
}

int main() {
	int T;
	scanf("%d", &T);
	while (T--) {
		scanf("%d %lld", &n, &k);
		for (int i = 1; i <= n; ++i) {
			scanf("%lld", a + i);
		}
		ll l = 1, r = 1e17, res = 0;
		while (r - l >= 0) {
			ll mid = (l + r) >> 1;
			if (check(mid)) {
				res = mid;
				l = mid + 1;
			} else {
				r =  mid - 1;
			}
		}
		printf("%lld\n", res * k);
	}
	return 0;
}

L. Divide The Students

题意：

有三类人，每类人有\(a, b, c\)个。

现在要将这三类人分成三组，使得第一类和第三类人不能在同一组，并且使得所有组的最大人数最少。

思路：

令\(a > c\)，那么将\(c\)单独放在一组，将\(a\)均分成两组，然后\(b\)每次选一个人数最少的组放。

代码：

view code

#include <bits/stdc++.h>
using namespace std;

int main() {
	int _T; scanf("%d", &_T);
	while (_T--) {
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
	//	int res = max((a + b + c + 2) / 3, min(a, c));
	//	printf("%d\n", res);
		if (a < c) swap(a, c);
		int A[3] = {a / 2, a - a / 2, c};
		while (b) {
			sort(A, A + 3);
			++A[0];
			--b;
		}
		printf("%d\n", max(A[0], max(A[1], A[2])));
	}
	return 0;
}

M. SmartGarden

题意：

给出一个\(n \cdot n\)的矩形，其中对角线和对角线下面一条线是墙，其他地方是蔬菜，类似这样：



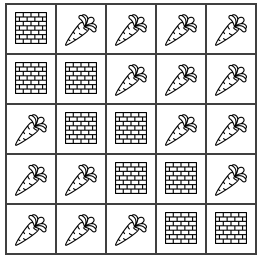
现在每次可以选择若干个行，若干个列，将这些行列相交的地方浇上水，次数最多为\(50\)次，并且不能浇到墙，并且每棵蔬菜都要被浇到。

N. Wires

题意：

给出\(n\)条边，点的标号在\([1, 10^9]\)，现在可以修改某条边的某个端点，使得这\(n\)条边所构成的图是一个连通块。

使得修改次数最少。

思路：

显然最少修改次数为连通块个数 - 1。

随便选取一个连通块出来，让其他连通块都连向这个连通块。

然后考虑每个连通块里：

• 如果有\(1\)度顶点，直接改掉这个\(1\)度顶点
• 那么没有\(1\)度顶点，那么必然有环，随便改掉环上的一条边即可

代码：

view code

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10, INF = 0x3f3f3f3f;
struct Hash {
	vector <int> a;
	void init() { a.clear(); }
	void add(int x) { a.push_back(x); }
	void gao() { sort(a.begin(), a.end()); a.erase(unique(a.begin(), a.end()), a.end()); }
	int get(int x) { return lower_bound(a.begin(), a.end(), x) - a.begin() + 1; }
}hs;
struct E {
	int u, v;
	E() {}
	E(int u, int v) : u(u), v(v) {}
}e[N];
struct node {
	int id, u, v;
};
vector <vector<node>> G;
vector <node> res;
int n, m, d[N], fa[N], vis[N], Insta[N], used[N], usede[N], F;
int find(int x) { return fa[x] == 0 ? x : fa[x] = find(fa[x]); }
void merge(int u, int v) {
	u = find(u); v = find(v);
	if (u != v) fa[u] = v;
}
void dfs(int u) {
	used[u] = 1;
	Insta[u] = 1;
	for (auto &it : G[u]) if (!usede[it.id]) {
		usede[it.id] = 1;
		int v = it.v;
		if (Insta[v]) {
			if (!F) {
				res.push_back({it.id, hs.a[it.u - 1], hs.a[0]});
				F = 1;
				return;
			}
		}
		if (used[v] == 0) {
			dfs(v);
		}
		if (F) return;
	}
	Insta[u] = 0;
}

int main() {
	int _T; scanf("%d", &_T);
	while (_T--) {
		scanf("%d", &n);
		hs.init();
		for (int i = 1, u, v; i <= n; ++i) {
			scanf("%d%d", &u, &v);
			hs.add(u); hs.add(v);
			e[i] = E(u, v);
			usede[i] = 0;
		}
		hs.gao();
		m = hs.a.size();
		for (int i = 1; i <= m; ++i) {
			d[i] = fa[i] = 0;
			vis[i] = 0;
			Insta[i] = used[i] = 0;
		}
		G.clear(); G.resize(m + 1);
		for (int i = 1; i <= n; ++i) {
			e[i].u = hs.get(e[i].u);
			e[i].v = hs.get(e[i].v);
			++d[e[i].u];
			++d[e[i].v];
			merge(e[i].u, e[i].v);
			int u = e[i].u, v = e[i].v;
			G[u].push_back({i, u, v});
			G[v].push_back({i, v, u});
		}
		int rt = 1, frt = find(rt);
		vis[frt] = 1;
		res.clear();
		for (int i = 1; i <= n; ++i) {
			int &u = e[i].u, &v = e[i].v;
			if (d[u] > d[v]) swap(u, v);
			int fu = find(u);
		    if (vis[fu]) continue;
			if (d[u] == 1) {
				res.push_back({i, hs.a[u - 1], hs.a[0]});
				vis[fu] = 1;
			}
		}
		for (int i = 1; i <= m; ++i) {
			int fi = find(i);
			if (vis[fi]) continue;
			F = 0;
			vis[fi] = 1;
			dfs(i);
		}
		int sze = res.size();
		printf("%d\n", sze);
		for (int i = 0; i < sze; ++i) {
			printf("%d %d %d\n", res[i].id, res[i].u, res[i].v);
		}
	}
	return 0;
}