P5020 货币系统

P5020 货币系统

题解

仔细分析。。。

这道题其实就是求所给数组中有多少个数字不能被该数组中的数字自由组合表示出来

比如样例1

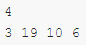
3,10 不能被该集合里的数字表示出来，所以他们组成目标集合

6=3+3   19=10+6+3

那么问题来了，只知道思路不会写（于是我们翻开题解）

solution 1

考虑到对于任意一个数字 x ，如果它能被集合里面的数字表示出来，并且表示它的数字中包含数字 a[i] ，那么 x-a[i] 一定也可以被集合里的数字表示出来

这就涉及到了集合的并集

can[i] 表示数字 i 能不能被表示出来（为什么用can而不是f而不是vis？？？因为惨）

can[i] = can[i] ∪ can[ i-a[k] ]

注意初始化 can[0]=1

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<queue>
#include<cstdlib>

using namespace std;

typedef long long ll;

inline int read(){
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return  ans;
}

const int maxn=;
int T,n,ans;
int can[maxn];
int a[];

int main()
{
    T=read();
    while(T--){
        memset(a,,sizeof(a));
        memset(can,,sizeof(can));
        can[]=;
        n=read();ans=n;
        for(int i=;i<=n;i++) a[i]=read();
        sort(a+,a+n+);
        for(int i=;i<=n;i++){
            if(can[a[i]]) ans--;
            else{
                for(int j=a[i];j<=maxn;j++)
                    can[j]=can[j]|can[j-a[i]];
            }
        }
        printf("%d\n",ans);
    }

    return ;
}

solution 2

可以完全背包一下

f[i] 表示数字 i 最多可以被几个数字表示出来

显然上一个做法的结论成立：考虑到对于任意一个数字 x ，如果它能被集合里面的数字表示出来，并且表示它的数字中包含数字 a[i] ，那么 x-a[i] 一定也可以被集合里的数字表示出来

f[i] = max( f[i] , f[i-a[k]]+1 )

那么只能被一个数字表示出来的，显然就是答案啦

注意初始化负无穷 这里用到了指针写法 f i l l 

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<queue>
#include<cstdlib>

using namespace std;

typedef long long ll;

inline int read(){
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return  ans;
}

const int maxn=;
int f[maxn],a[];
int T,n,ans=;

int main()
{
    T=read();
    while(T--){
        memset(a,,sizeof(a));
        fill(f + , f + maxn + , -);
//        memset(f,-0x7f,sizeof(f));
        f[]=;
        ans=;

        n=read();
        for(int i=;i<=n;i++) a[i]=read();

        sort(a+,a+n+);

        for(int i=;i<=n;i++)
          for(int j=a[i];j<=maxn;j++)
             f[j]=max(f[j],f[j-a[i]]+);

        for(int i=;i<=n;i++)
            if(f[a[i]]==)
                ans++;

        printf("%d\n",ans);
    }
    return ;
}