P3384 【模板】树链剖分 题解&&树链剖分详解

题外话：

一道至今为止做题时间最长的题：

begin at 8.30A.M

然后求助_yjk dalao后

最后一次搞取模：

awsl。

正解开始：

题目链接。

树链剖分，指的是将一棵树通过两次遍历后将一棵树分成重链，轻边的过程。

我们定义：

重儿子：每个点的子树中，子树大小(即节点数)最大的子节点

轻儿子：除重儿子外的其他子节点

重边：每个节点与其重儿子间的边

轻边：每个节点与其轻儿子间的边

重链：重边连成的链

轻链：轻边连成的链（目前没用到过，还是太菜）

于是乎，我们来举个栗子：

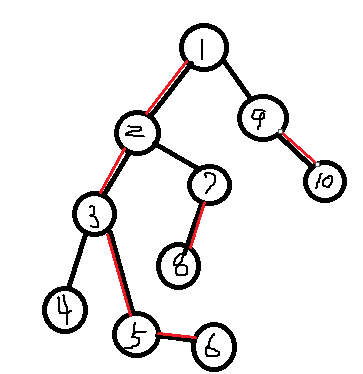
其中，红色边为重边，自然，它们组成的链就是重链喽。你可以按照定义从根节点往下人脑dfs（？？？）一遍模拟过程，方便理解dfs代码。

窝们发现：重链和轻边交替出现（没什么用）。

然后，理解完上面的部分呢，我们先安排一下两个dfs，用来剖分整棵树以及dfs过程中顺便搞一下其他东西（面向题目编程）。。

第一个dfs：

作用：求出每一个节点的深度dep，定义father指针fa[]指向自己的父亲节点，求出子树的大小size并顺便找到重儿子son

代码如下：

inline void dfs1(int now,int f,int deep)
{
    dep[now]=deep;//now指的是当前节点
    fa[now]=f;//指向父亲节点
    size[now]=;//加上自己
    int maxn=-,maxson=;//初始
    for(int i=hea[now];i;i=edge[i].next)//链式存图
    {
        int v=edge[i].to;
        if(v==f)continue;//不要再找回去了。。
        dfs1(v,now,deep+);//先把自己子树的信息确定好
        size[now]+=size[v];//这时候size[v]已经确定了，我们就往上统计大小
        if(size[v]>maxn)maxson=v,maxn=size[v];//根据定义，求出子树最大的儿子重儿子
    }
    son[now]=maxson;//for完了就找最大的赋值
}

到这里，我们成功地把重儿子都给找了出来，下一步差连成链了。

第二遍dfs：

在第一遍dfs已经找到了重儿子的基础上，我们将每一条重链上的节点的编号弄成相邻的，也就是一条重链上节点编号相邻，这样保证了一条重链可以被划分为一个区间，方便以后的跳跃和区间查询操作。

自然地，我们需要在遍历时先遍历重儿子来保证区间顺序相连。

代码如下：

inline void dfs2(int now,int ttop)//top代表一个重链的头，也就是dfs序最小的那个
{
    dfn[now]=++num2;//num1在链式前向星中用到了。233
    a0[num2]=a[now];//新的顺序，来使一条重链上节点编号相邻
    top[now]=ttop;//记指针指向一条重链中的链头。
    if(!son[now])return;//如果没儿子，直接返回了
    dfs2(son[now],ttop);//先搜重儿子
    for(int i=hea[now];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v==fa[now]||v==son[now])continue;//father和son已经搜过了
        dfs2(v,v);//以当前节点为重链头部搜下去，而不再是ttop
    }
}

树链剖分主体部分完结。。。（大雾）

因为最重要的部分不是剖分而是与其他知识结合。。（霾）

最重要的部分（也是我一直不懂的部分）：

关于询问树上两点路径权值之和以及修改权值之和的问题：

自然，我们要把路径检索出来。。

众所周知，对于一棵树，任意两个点间，有且仅有一条路径，且这条路径经过他们的LCA。这说明，在查询和修改两点路径时，我们可以将树链剖分求lca与线段树区间修改有机结合？。

怎么结合呢：

注意一下描述：

对于我们要求的两个点的lca，容易想到加速的方法为：顺着一条树链往上跳，直接跳到树链头部，这样一次能够跨越整条树链。具体的方法：

1.找到深度更大的那个节点。

2.如果两个节点所在重链的头部不为同一个节点的话，说明他们的lca比他们的树链头部的深度还要浅，那么我们就可以将深度较深的节点跳到他的上一个重链的尾部（也就是x=fa[top[x]]）来继续查找，这样我们就可以跳过一整条重链了。

（2的话呢，使劲循环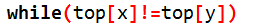

3.当不再满足上面的条件，就说明他们已经在一条重链中了。那么自然的，深度更小，在上面的节点为他们的lca。

那么，顺着这个思路，我们在跳过重链的时候顺便query一下整个重链，一直query到lca。就完成了整条路径上的查询。

错！

你会发现，还差那么一段没有被覆盖上（绿色）：

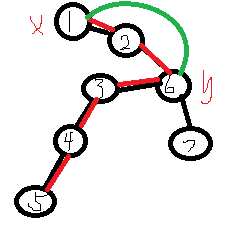
那么，我们只需要这样一段指令：

再把x和y相差的那一段区间再查一下就可以了。

路径查询部分代码：

inline int querylj(int x,int y)
{
    int ans=;
    while(top[x]!=top[y])//还没有跳到同一个树链上的话
    {
        if(dep[top[x]]<dep[top[y]])swap(x,y);//把x作为深度更深的节点方便处理
        ans+=query(,,n,dfn[top[x]],dfn[x])%p;//一次查询从链头到尾部
        ans%=p;
        x=fa[top[x]];//跳跃
    }
    if(dep[x]>dep[y])swap(x,y);
    ans+=query(,,n,dfn[x],dfn[y])%p;//最后一段的查询
    return ans%p;
}

至于区间路径修改，一个原理。

就是把query函数换成update区间修改，然后函数没有返回值罢了。

代码：

inline void queryupdlj(int x,int y,int k)//注释就不加了
{
    int ans=;
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        update(,,n,dfn[top[x]],dfn[x],k);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    update(,,n,dfn[x],dfn[y],k);
}

至于子树修改，更简单了：

自然而然的，因为dfs续的缘故，我们不难想到一个子树内所有的节点的dfs序都是一个连续区间，区间开头是子树根节点的dfn，区间长度为子树大小size，那么对应的区间就为（设根节点为x的话）x到x+size[x]-1。

所以这就是个简单的区间修改，一步到位。

inline int queryson(int x)//查询
{return query(,,n,dfn[x],dfn[x]+size[x]-);}
inline void queryupdson(int x,int k)//修改{update(1,1,n,dfn[x],dfn[x]+size[x]-1,k);}

此题代码：

#include<cstdio>
#include<cstring>
#include<queue>
#include<cmath>
#include<iostream>
#define N 100003
using namespace std;
void swap(int &x,int &y){int temp=x;x=y,y=temp;}
int read()
{
    int ans=;
    char ch=getchar(),last=' ';
    while(ch<''||ch>'')last=ch,ch=getchar();
    while(ch>=''&&ch<='')ans=(ans<<)+(ans<<)+ch-'',ch=getchar();
    return last=='-'?-ans:ans;
}
struct edg{
    int next,to;
}edge[N*];
int n,fr,to,m,r,p,a0[N],a[N],a1[N*],son[N],top[N],size[N],fa[N],dep[N],dfn[N],num1,num2,hea[N],lazy[N*];
inline void add(int from,int to){num1++;edge[num1]=(edg){hea[from],to};hea[from]=num1;}
inline void pushdown(int rt,int lenn){
    lazy[rt<<]+=lazy[rt]%p;
    lazy[rt<<|]+=lazy[rt]%p;
    a1[rt<<]+=lazy[rt]*(lenn-(lenn>>))%p;
    a1[rt<<|]+=lazy[rt]*(lenn>>)%p;
    a1[rt<<]%=p;
    a1[rt<<|]%=p;
    lazy[rt]=;
}
inline void build(int l,int r,int now)
{
    if(l==r)
    {
        a1[now]=a0[l];a1[now]%=p;return;
    }
    int mid=(l+r)>>;
    build(l,mid,now<<);
    build(mid+,r,now<<|);
    a1[now]=(a1[now<<]+a1[now<<|])%p;
}
void update(int now,int l,int r,int L,int R,int k)
{
    if(l>=L&&r<=R){lazy[now]+=k%p;a1[now]+=k*(r-l+)%p,a1[now]%=p;return;}
    if(lazy[now])pushdown(now,r-l+);
    int mid=(l+r)>>;
    if(L<=mid)update(now<<,l,mid,L,R,k);
    if(R>mid)update(now<<|,mid+,r,L,R,k);
    a1[now]=(a1[now<<]+a1[now<<|])%p;
//  printf("1次upd\n");
}
inline int query(int now,int l,int r,int L,int R)
{
    int ans=;
    if(l>=L&&r<=R){ans+=a1[now]%p,ans%=p;return ans;}
    if(lazy[now])pushdown(now,r-l+);
    int mid=(l+r)>>;
    if(L<=mid)ans+=query(now<<,l,mid,L,R),ans%=p;
    if(R>mid)ans+=query(now<<|,mid+,r,L,R),ans%=p;
    return ans;
//  printf("1次query\n");
}
inline void dfs1(int now,int f,int deep)
{
    dep[now]=deep;
    fa[now]=f;
    size[now]=;
    int maxn=-,maxson=;
    for(int i=hea[now];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v==f)continue;
        dfs1(v,now,deep+);
        size[now]+=size[v];
        if(size[v]>maxn)maxson=v,maxn=size[v];
    }
    son[now]=maxson;
}
inline void dfs2(int now,int ttop)
{
    dfn[now]=++num2;
    a0[num2]=a[now];
    top[now]=ttop;
    if(!son[now])return;
    dfs2(son[now],ttop);
    for(int i=hea[now];i;i=edge[i].next)
    {
        int v=edge[i].to;
        if(v==fa[now]||v==son[now])continue;
        dfs2(v,v);
    }
}
inline int querylj(int x,int y)
{
    int ans=;
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        ans+=query(,,n,dfn[top[x]],dfn[x])%p;
        ans%=p;
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    ans+=query(,,n,dfn[x],dfn[y])%p;
    return ans%p;
}
inline void queryupdlj(int x,int y,int k)
{
    int ans=;
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        update(,,n,dfn[top[x]],dfn[x],k);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    update(,,n,dfn[x],dfn[y],k);
}
inline int queryson(int x){return query(,,n,dfn[x],dfn[x]+size[x]-);}
inline void queryupdson(int x,int k){update(,,n,dfn[x],dfn[x]+size[x]-,k);}
int main()
{
    n=read(),m=read(),r=read(),p=read();
    for(int i=;i<=n;i++)
        a[i]=read();
    for(int i=;i<=n-;i++)
    {
        fr=read(),to=read();
        add(fr,to);add(to,fr);
    }
    dfs1(r,,);
    dfs2(r,r);
    build(,n,);
    for(int i=;i<=m;i++)
    {
        int k,x1,y1,z1;
        k=read();
        if(k==){
            x1=read(),y1=read(),z1=read();
            queryupdlj(x1,y1,z1);
        }
        else if(k==){
           x1=read();y1=read();
            printf("%d\n",querylj(x1,y1)%p);
        }
        else if(k==){
            x1=read();y1=read();
            queryupdson(x1,y1);
        }
        else{
            x1=read();
            printf("%d\n",queryson(x1)%p);
        }
    }
}

心力交猝。。

完结。

希望对各位有所帮助，有什么不对的地方评论指出。