Leetcode题解（33）

113. Path Sum II

题目

分析：

主要考察二叉树深度优先遍历（DFS），递归调用当前节点的左右结点即可，代码如下（copy网上）：

 /**
  * Definition for binary tree
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
  * };
  */
 class Solution {
 private:
     vector<vector<int> > ret;
 public:
     void dfs(TreeNode *node, int sum, int curSum, vector<int> a)
     {
         if (node == NULL)
             return;

         if (node->left == NULL && node->right == NULL)
         {
             if (curSum + node->val == sum)
             {
                 a.push_back(node->val);
                 ret.push_back(a);
             }
             return;
         }

         a.push_back(node->val);
         dfs(node->left, sum, curSum + node->val, a);
         dfs(node->right, sum, curSum + node->val, a);
     }

     vector<vector<int> > pathSum(TreeNode *root, int sum) {
         // Start typing your C/C++ solution below
         // DO NOT write int main() function
         ret.clear();
         vector<int> a;
         dfs(root, sum, , a);
         return ret;
     }
 };

上面的方法中，采用了递归，代码简单也利于理解，如果要是不采用递归该怎么求解呢？

如果不采用递归，就需要在迭代过程中“回溯”，也就需要保存当前节点左右子节点是否已经遍历过，如果没有遍历，则继续往下遍历，如果都遍历过了，则往其父节点回溯

代码如下：

 /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
  * };
  */
 class Solution {
 public:
     vector<vector<int>> pathSum(TreeNode* root, int sum) {
         vector<vector<int>> res;
         vector<int> temp;
         vector<TreeNode*> myStack;//用vector模拟stack
         stack<bool> isVisitedLeft;//记录左节点是否访问过
         stack<bool> isVisitedRight;//记录右节点是否访问过
         TreeNode *top;
         int index;
         int count=;
         if(NULL == root)
             return res;
         if(root->left == NULL && root->right == NULL)
         {
             if(root->val == sum)
             {
                 temp.push_back(root->val);
                 res.push_back(temp);
             }

             return res;
         }
         myStack.resize();
         myStack[] = root;
         isVisitedLeft.push(false);
         isVisitedRight.push(false);
         index=;
         count += root->val;
         while(index>=)
         {
             top = myStack[index];
             if(!(isVisitedLeft.top()))//左节点没有被访问
             {
                 isVisitedLeft.pop();
                 isVisitedLeft.push(true);
                 if(top->left != NULL)
                 {
                     myStack[index+]= top->left;//插入左节点
                     isVisitedLeft.push(false);//该节点左右节点都没被访问过
                     isVisitedRight.push(false);
                     index++;
                     count+=top->left->val;
                 }

             }
             else if(!(isVisitedRight.top()))
             {
                 isVisitedRight.pop();
                 isVisitedRight.push(true);
                 if(top->right != NULL)
                 {
                     myStack[index+]= top->right;
                     isVisitedLeft.push(false);//该节点左右节点都没被访问过
                     isVisitedRight.push(false);
                     index++;
                     count+=top->right->val;
                 }    

             }
             else
             {
                 if(count == sum && top->left == NULL && top->right == NULL)
                 {
                     temp.clear();
                     //for(int i=0;i<myStack.size();i++)不能这样写
                     for(int i=;i<=index;i++)
                     {
                         temp.push_back(myStack[i]->val);//这里就知道为啥用vector模拟stack，主要是为了遍历方便，也可以用stack，只不过遍历stack需要逐个出栈
                     }
                     res.push_back(temp);
                 }

                 count -=top->val;
                 index--;
                 isVisitedLeft.pop();
                 isVisitedRight.pop();

             }
         }
         return res;
     }
 };

--------------------------------------------------------------------------------分割线--------------------------------------------------------------------------------

114. Flatten Binary Tree to Linked List

题目

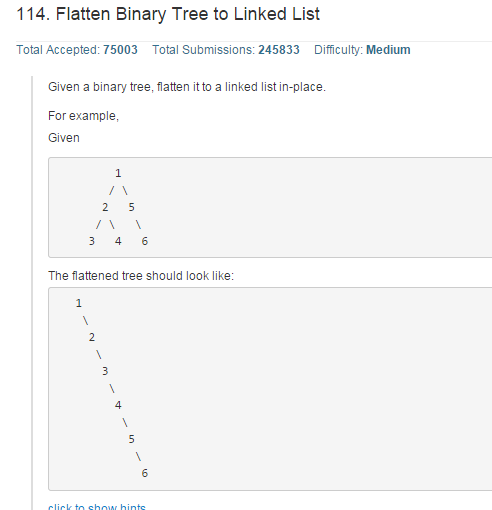
分析：

根据题目的例子可以发现，最终得到的结果其实是二叉树前序遍历得到的序列顺序。因此可以仿照前序遍历的递归思想进行操作，代码如下：

代码中有一个lastNode 指针，用于指向当前链表的最后一个节点。

 /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
  * };
  */
 class Solution {
 public:
     TreeNode* lastNode;
     void flatten(TreeNode* root) {
         if(NULL == root)
             return;
         lastNode = root;
         preOrder(root);
     }
     void preOrder(TreeNode* root)
     {
         if(root== NULL)
         {
             return ;
         }
         TreeNode *temp=NULL;
         lastNode = root;
         temp = root->right;//切断右子树，用temp指向右子树
         root->right = root->left;
         root->left = NULL;
         preOrder(root->right);
         lastNode->right = temp;//右子树的所有节点是lastNode节点之后的
         preOrder(temp);
     }
 };

如果采用非递归的，则需要一个stack，但是不符合题目要求：在本地处理节点（in-place）。