Machine Learning - week 3
Classification
使用线性回归来分类,会很不准确。并且,它的范围也会超出 {0, 1}。所以使用下面的逻辑回归模型。
Hypothesis representation
线性回归中 hθ(x) = θTx,而在逻辑回归中,我们想要 hθ(x) ∈ [0, 1]。对结果进行双曲化处理:
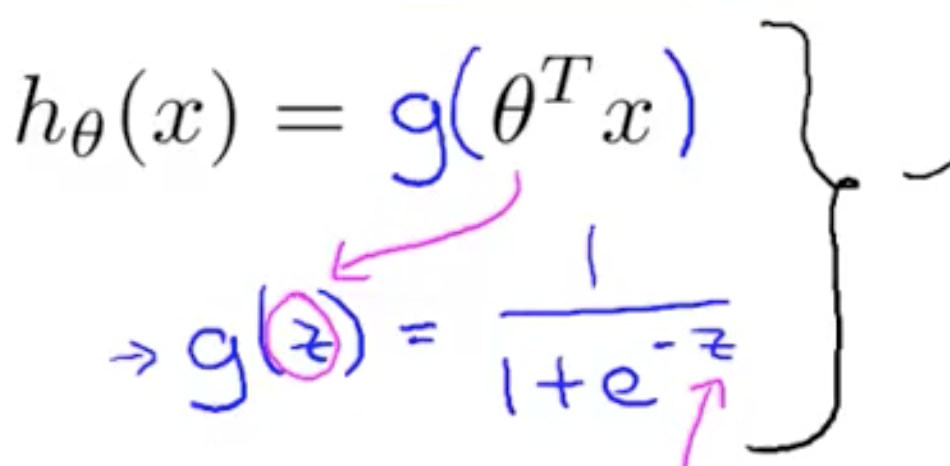
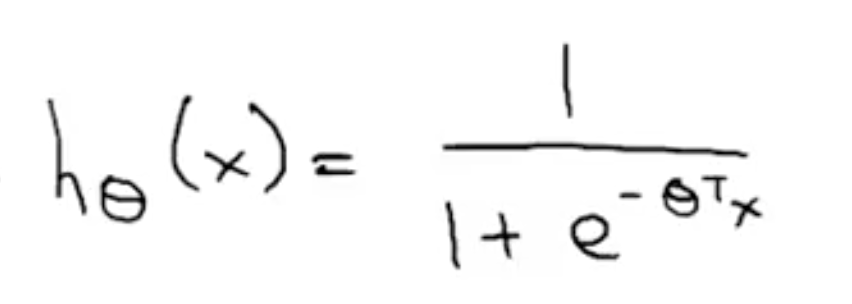
,图象如右图: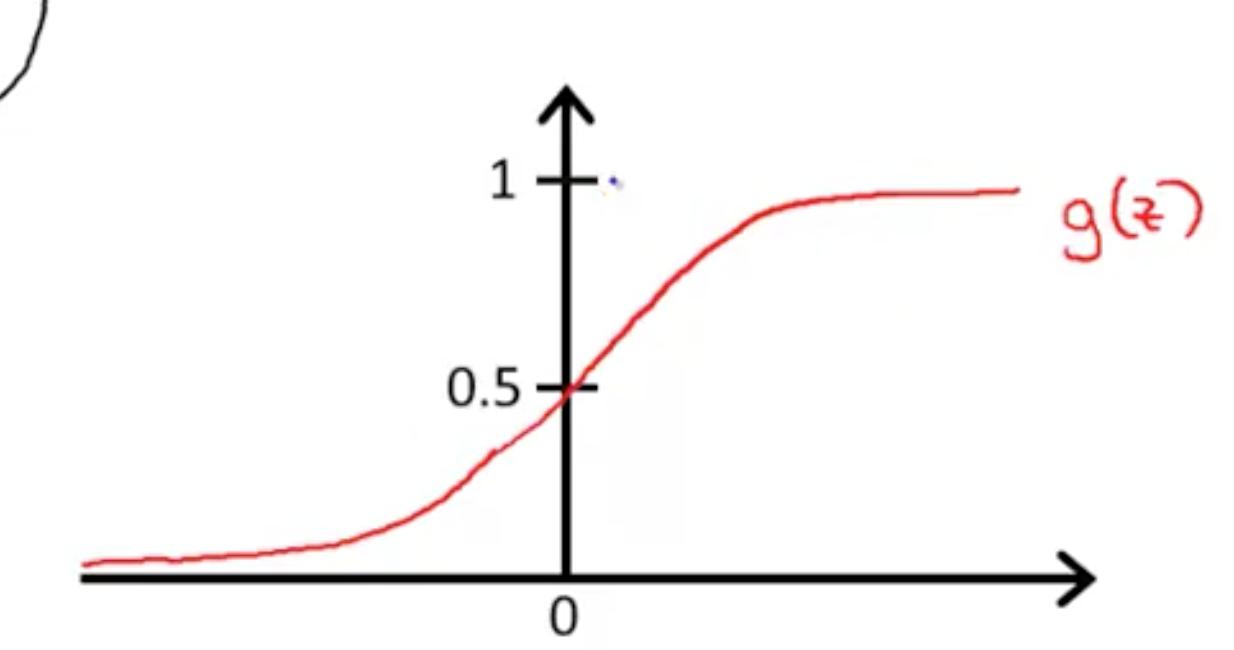 ,范围是 (0, 1)。
,范围是 (0, 1)。
在线性回归中,hθ(x) 就表示 y 的值。在逻辑回归中,表示『基于输入的 x,y=1 的概率是多少』。用数学形式表示: 。
。
Desicion boundary
逻辑回归中, hθ(x) 是属于 (0, 1) 范围内的连续的值。但我们的分类结果只有 0 或者 1,所以就需要一个决策边界。这里,取平均值, y = 0.5。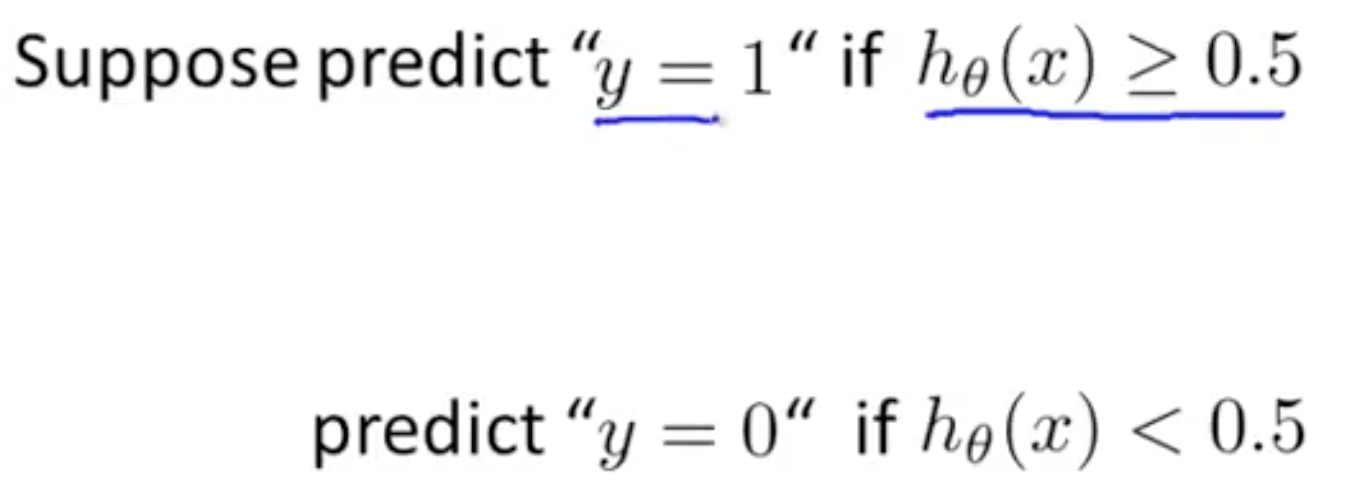 。从上方的双曲线图中可以看出,当 z > 0,y=1,即 θTx >= 0 时,hθ(x) >= 0.5。将区域分为 y=0 和 y=1 的两个区域。
。从上方的双曲线图中可以看出,当 z > 0,y=1,即 θTx >= 0 时,hθ(x) >= 0.5。将区域分为 y=0 和 y=1 的两个区域。
决策边界是针对与 θ 的属性,所以 θ 不同,决策边界也不同。
非线性的决策边界
当 hθ(x) 是多项式的时候,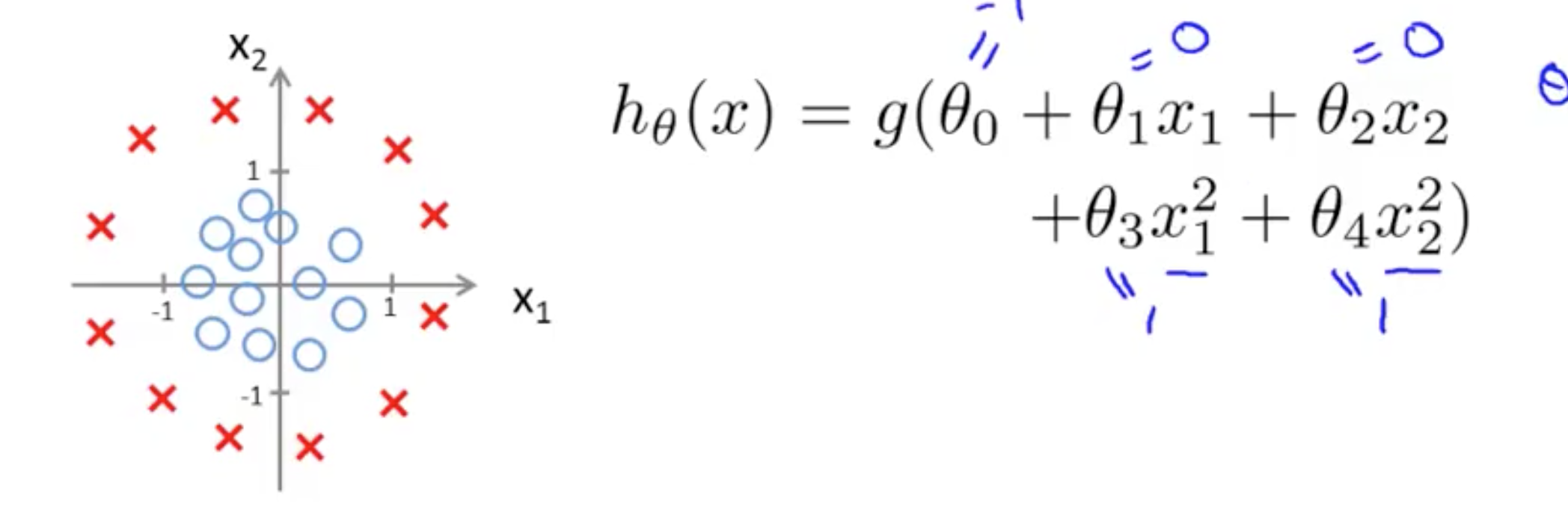 。
。
当多项式更加复杂的时候,决策边界的形状也会更加复杂。
Cost Function

当 y = 1 时,如果 hθ(x) = 0,那么 cost 接近无限大。因为你预测不是恶性肿瘤,但实际上是恶性肿瘤。同样,如果不是恶性肿瘤,你预测 y = 1 的概率越接近 1,那么误差越小。
y = 0 时的情况同理可得。
化简的 Cost Function 和 Gradient Descent
化简后(通过遍历所有情况能够证明)
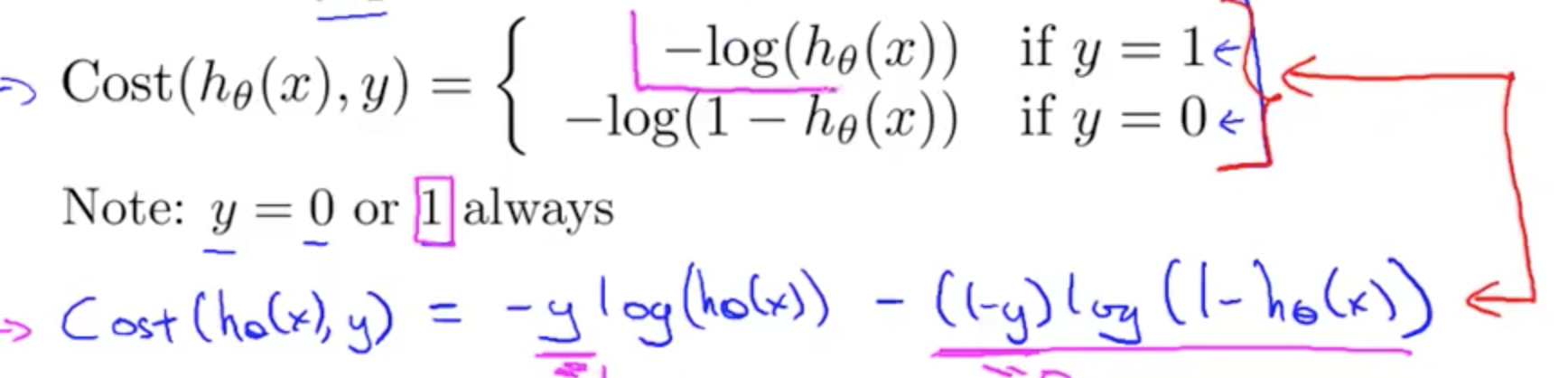
J(θ) 为
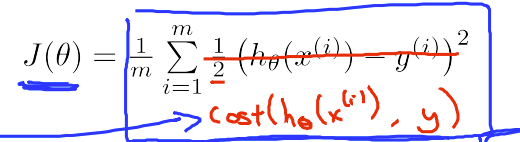
Gradient Descent

Logistic Regression 与 Linear Regression 在 Gradient Descent 上的不同,就是 hθ(x) 的不同。
用矩阵计算为:
grad = (X' * (h - y)) / m;
这里是求和,所以最终是 1*1,所以转置成这样的形式 [1 * n] * [n * 1]。
Advanced Optimization
使用更高级的算法,不需要手动选择 learning rate;通常比 gradient descent 更快;缺点是更复杂。
可以使用库直接调用这些算法,不需要深入理解它们。

% 我们传入了 GradObj,最大循环次数为 100 次
octave:1> options = optimset('GradObj', 'on', 'MaxIter', '100')
options = scalar structure containing the fields: GradObj = on
MaxIter = 100 octave:2> initialTheta = zeros(2,1 )
initialTheta = 0
0
jVal 表示 j(θ) 的计算方法
gradient 表示对应 θ 的计算方法(求导)
Multiclass Classfication
大于 2 个类别,如邮件分类:工作、朋友、家庭。
使用 one-vs-rest 方法。
假设有 3 类,我们将测试数据分为 C32 类别,把一类看作 positive,其他类看做 negative。这样我们就能得到三个 h(θ)
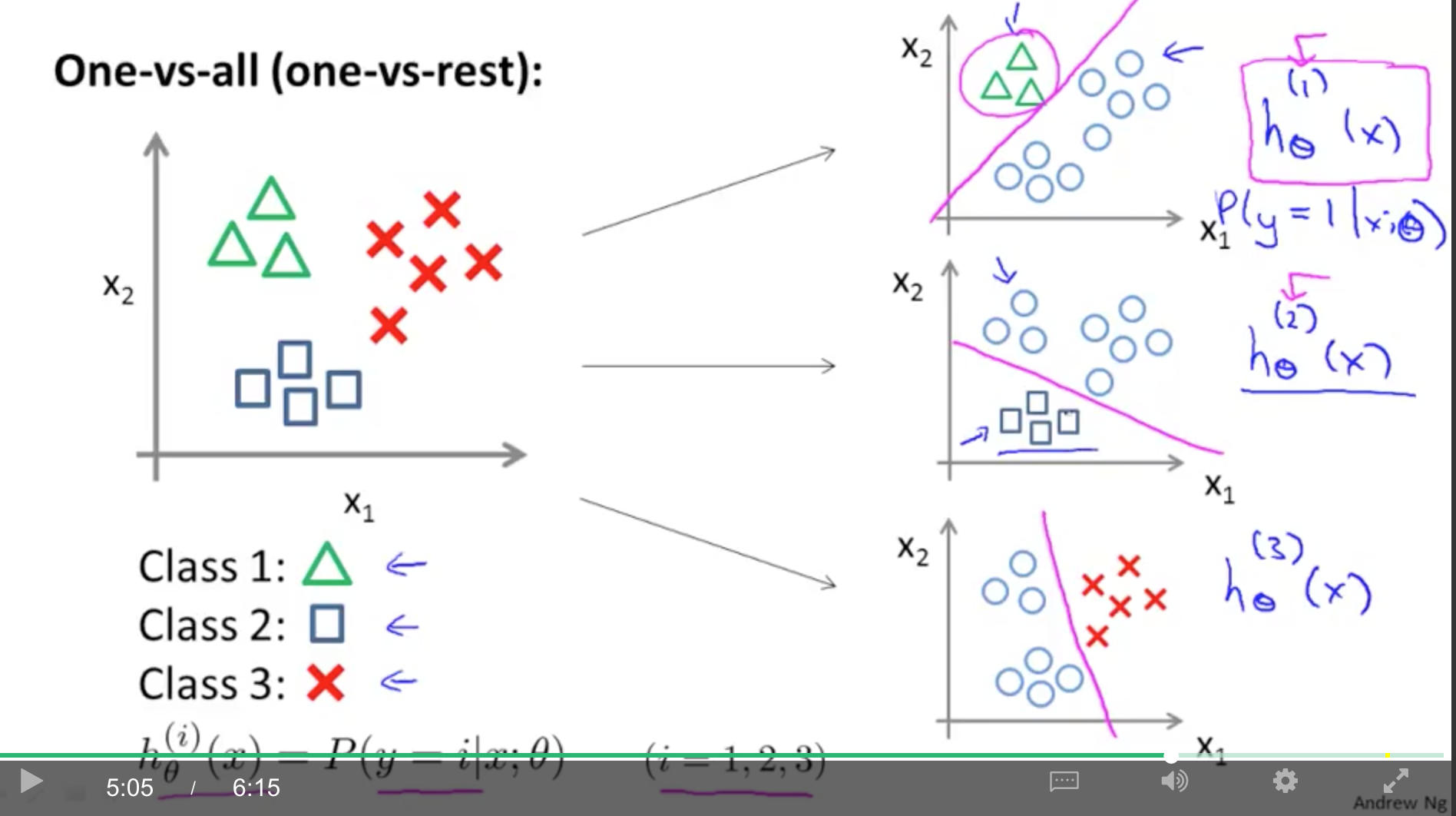
在预测时,由于有三个 h(θ) 函数,所以有三个结果。一般是取概率最大的作为最终预测结果。
习题
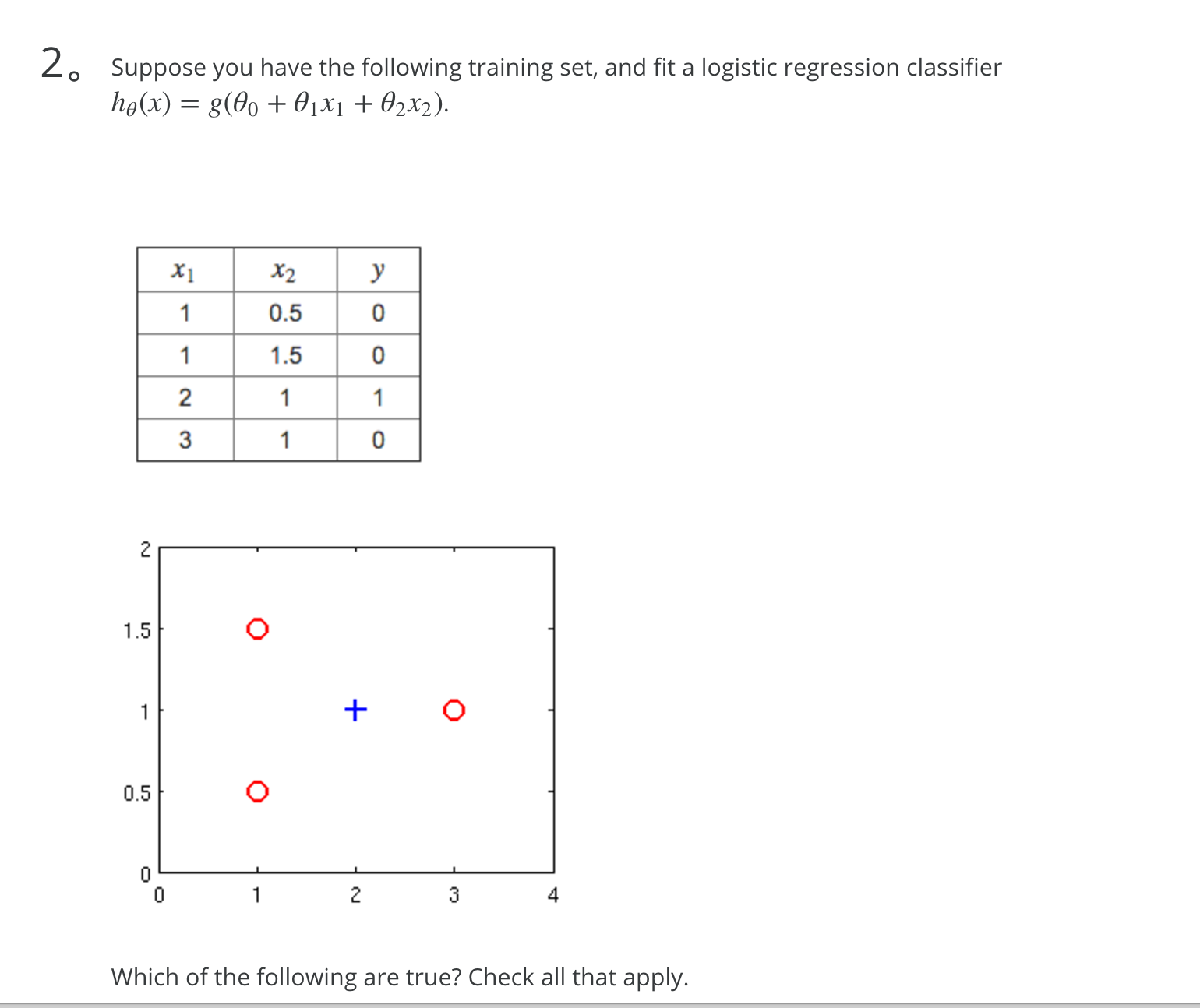

从图中可以可以看出,应该是一个圆把蓝色的圈住,所以应该有两个 x2
1. 如何判断是否 convex,gradient 什么情况下(能/否) converge
- 判断 convex 要由数学证明完成,我们是选择别人证明好的 cost function,这里不做证明。
- 确保 learning rate α 被设置合适。
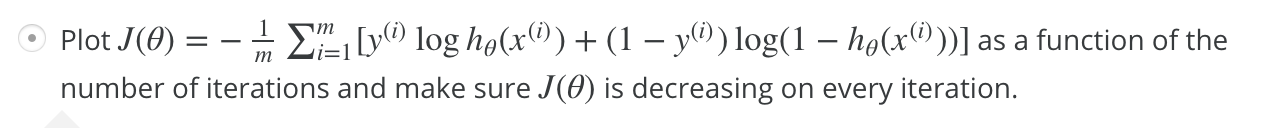
2. 增加多项式 features 可以增加对训练数据的匹配。更匹配的意思是:使曲线与数据更贴近。
对。
3. 能否被直线分割为两段有什么区别?对 converge 有影响吗?
不知道。应该没有
non-linear decision boundaries

4. linear regression 与 logistic regeress 的区别?两者会相同吗?在什么情况下会相同?
Gradient Descent 的公式是一样的,但是 hθ(x) 不一样

为什么 hθ(x) 要不一样呢?
想要 0 < hθ(x) < 1,所以定义了 Logistic function (sigmoid function)。
还是有错误。

有错误
第二个选项:应该对的。J(θ) 表示的是误差。
第三个选项:没有理解清楚。算错误的
第四个选项:

没有提到 local minimum,但我认为有这个原因。
如何用 vector 表示 J(θ)
3. 
从课件中查到公式为  ,所以 3、4 是对的。
,所以 3、4 是对的。
1 是错误的。
θTx - y(i) 为 n * 1 的 vector。乘以 x 第 i 行。应该是乘以 x 第 i 行第 j 个,其中 j 是不变的。所以是错误。

第一个,对的
第二个,意思是:允许你对于每个 y 来自固定的、离散的几组值。对的。
第三个,对。范围就是 >= 0 不会变
第四个,对
存在错误。
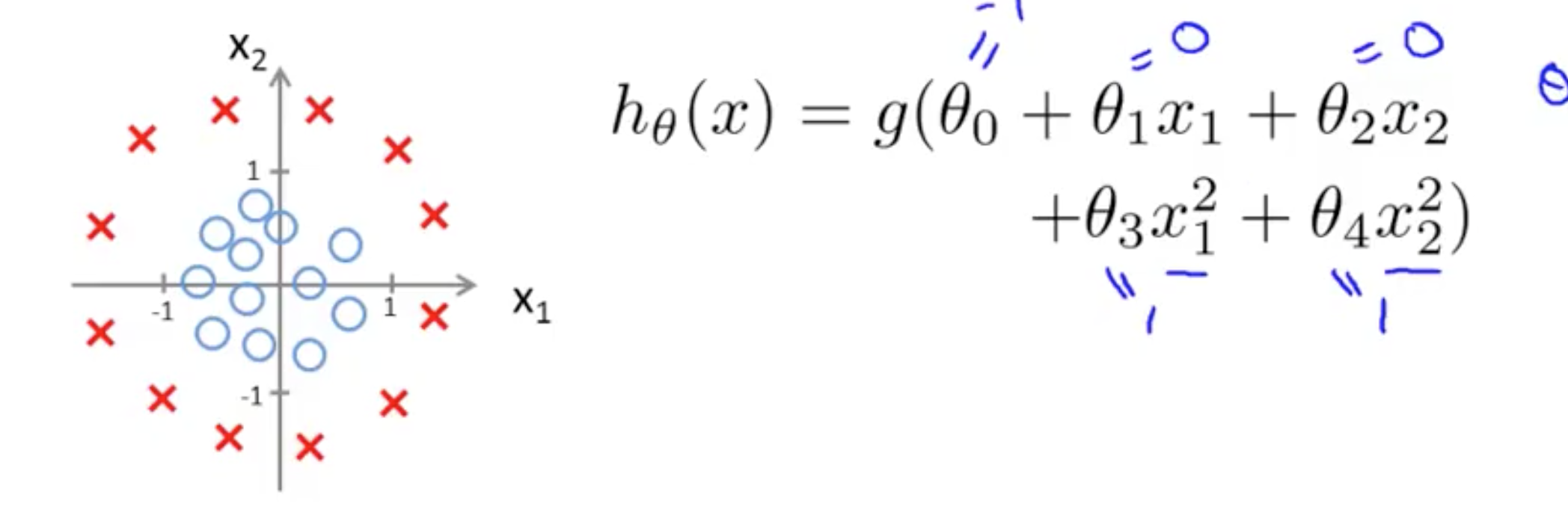
Machine Learning - week 3的更多相关文章
- 【Machine Learning】KNN算法虹膜图片识别
K-近邻算法虹膜图片识别实战 作者:白宁超 2017年1月3日18:26:33 摘要:随着机器学习和深度学习的热潮,各种图书层出不穷.然而多数是基础理论知识介绍,缺乏实现的深入理解.本系列文章是作者结 ...
- 【Machine Learning】Python开发工具:Anaconda+Sublime
Python开发工具:Anaconda+Sublime 作者:白宁超 2016年12月23日21:24:51 摘要:随着机器学习和深度学习的热潮,各种图书层出不穷.然而多数是基础理论知识介绍,缺乏实现 ...
- 【Machine Learning】机器学习及其基础概念简介
机器学习及其基础概念简介 作者:白宁超 2016年12月23日21:24:51 摘要:随着机器学习和深度学习的热潮,各种图书层出不穷.然而多数是基础理论知识介绍,缺乏实现的深入理解.本系列文章是作者结 ...
- 【Machine Learning】决策树案例:基于python的商品购买能力预测系统
决策树在商品购买能力预测案例中的算法实现 作者:白宁超 2016年12月24日22:05:42 摘要:随着机器学习和深度学习的热潮,各种图书层出不穷.然而多数是基础理论知识介绍,缺乏实现的深入理解.本 ...
- 【机器学习Machine Learning】资料大全
昨天总结了深度学习的资料,今天把机器学习的资料也总结一下(友情提示:有些网站需要"科学上网"^_^) 推荐几本好书: 1.Pattern Recognition and Machi ...
- [Machine Learning] Active Learning
1. 写在前面 在机器学习(Machine learning)领域,监督学习(Supervised learning).非监督学习(Unsupervised learning)以及半监督学习(Semi ...
- [Machine Learning & Algorithm]CAML机器学习系列2:深入浅出ML之Entropy-Based家族
声明:本博客整理自博友@zhouyong计算广告与机器学习-技术共享平台,尊重原创,欢迎感兴趣的博友查看原文. 写在前面 记得在<Pattern Recognition And Machine ...
- machine learning基础与实践系列
由于研究工作的需要,最近在看机器学习的一些基本的算法.选用的书是周志华的西瓜书--(<机器学习>周志华著)和<机器学习实战>,视频的话在看Coursera上Andrew Ng的 ...
- matlab基础教程——根据Andrew Ng的machine learning整理
matlab基础教程--根据Andrew Ng的machine learning整理 基本运算 算数运算 逻辑运算 格式化输出 小数位全局修改 向量和矩阵运算 矩阵操作 申明一个矩阵或向量 快速建立一 ...
- Machine Learning
Recently, I am studying Maching Learning which is our course. My English is not good but this course ...
随机推荐
- redis基础二
前面已经学习了redis的基本的命令行操作和数据类型,下面开始redis一些有趣的功能. 订阅和发布机制 定义:发布者相当于电台,订阅者相当于客户端,客户端发到频道的消息,将会被推送到所有订阅此频道的 ...
- Python中import机制
Python语言中import的使用很简单,直接使用import module_name语句导入即可.这里我主要写一下"import"的本质. Python官方定义:Python ...
- Mac下nvm管理node.js版本问题
本篇文章主要是针对已经安装了node.js和nvm管理工具小伙伴遇到的问题. 管理工具有两个,一个是nvm,还有一个是nnvm的好处就是可以管理多个node版本,而且可以切换想要的版本,可以安装一个稳 ...
- selenium 封装
周末无聊 在家封装一个pyselenium.可能这些封装大家都会使用,但是我还是根据我自己的习惯去选择性的去封装一些在我工作中用的,这样的话,我就不用去看selenium的api的,我可以根据我自己的 ...
- vue基础学习(二)
02-01 vue事件深入-传参.冒泡.默认事件 <div id="box"> <div @click="show2()"> < ...
- Kettle中忽略错误行继续执行
在kettle执行的过程中,如果遇到错误,kettle会停止运行.在某些时候,并不希望kettle停止运行,所以就要处理下这些错误行. 例如这两天发现在一个转换中,总数出现一些不规则数据,这些数据一出 ...
- javascript字符串与数组转换汇总
本文给大家分享的是Js中字符串转换成数组,数组转换成字符串的函数,十分的简单实用,有需要的小伙伴可以参考下. 数组转字符串 1.join()方法 ? 1 2 3 4 var s= ["a&q ...
- 【读书笔记】A Swift Tour
素材:A Swift Tour 推荐下载Playground:Download Playground objc 自己较为熟悉,想熟悉下风头正劲的 swift.就先从官方的入门手册开始撸. 每一小节,我 ...
- Tengine 安装配置全过程(nginx 同理)
1.安装必要的编译环境好 yum update yum install gcc gcc-c++ autoconf automake 2.安装需要的组件 A.PCRE PCRE(Perl Compati ...
- S2 深入.NET和C#编程 一: 深入C#.NET框架
深入C#.NET框架 1..NET框架 之一 推荐一个代码管理平台,博客发布平台 git 之前的复习: 学习的网站: git github.com 2.类和对象的关系 Dept de ...
