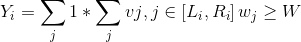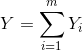[NOIP 2011]聪明的质监员
聪明的质监员
题目
小 T 是一名质量监督员,最近负责检验一批矿产的质量。这批矿产共有n个矿石,从 1 到n逐一编号,每个矿石都有自己的重量wi以及价值vi。检验矿产的流程是:
1. 给定 m个区间[Li,Ri];
2. 选出一个参数W;
3. 对于一个区间[Li,Ri],计算矿石在这个区间上的检验值Yi:
j是矿石编号。
这批矿产的检验结果Y为各个区间的检验值之和。即:
若这批矿产的检验结果与所给标准值 S 相差太多,就需要再去检验另一批矿产。小 T 不想费时间去检验另一批矿产,所以他想通过调整参数 W 的值,让检验结果尽可能的靠近标准值 S,即使得S−Y的绝对值最小。请你帮忙求出这个最小值。
INPUT
输入文件 qc.in。
第一行包含三个整数n,m,S,分别表示矿石的个数、区间的个数和标准值。
接下来的n 行,每行2 个整数,中间用空格隔开,第i+1 行表示i 号矿石的重量wi 和价值vi 。
接下来的m 行,表示区间,每行2 个整数,中间用空格隔开,第i+n+1 行表示区间[Li,Ri]的两个端点Li 和Ri。注意:不同区间可能重合或相互重叠。OUTPUT
输出文件名为qc.out。
输出只有一行,包含一个整数,表示所求的最小值。SAMPLE
INPUT
5 3 15
1 5
2 5
3 5
4 5
5 5
1 5
2 4
3 3OUTPUT
10
EXPLAIN
当W 选4 的时候,三个区间上检验值分别为20、5、0,这批矿产的检验结果为25,此时与标准值S 相差最小为10。
解题报告
考试时打了暴力- -,本来想到二分的,结果脑子一抽,以为单峰性,又不会打三分,只能爆炸- -
正解:
二分答案加验证
容易知道,当W增大时,满足条件的wi数目会减少,从而v会减少,我们就可以用这个作为二分条件,进行二分
在进行验证时,可以根据W建前缀和数组,以保证查询时的复杂度,剩下的就很简单了= =
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long L;
inline L read(){
L sum();
char ch(getchar());
for(;ch<''||ch>'';ch=getchar());
for(;ch>=''&&ch<='';sum=sum*+(ch^),ch=getchar());
return sum;
}
L ans(0x7fffffffffffffffLL),sum[],quan[],s;
int n,m;
int edge_mn(0x7fffffff),edge_mx();
int w[],v[];
int l[],r[];
inline L my_min(L a,L b){
return a<b?a:b;
}
inline L my_max(L a,L b){
return a>b?a:b;
}
inline void ST(int x){
sum[]=quan[]=;
for(int i=;i<=n;i++){
sum[i]=sum[i-],quan[i]=quan[i-];
if(w[i]>=x)
sum[i]++,quan[i]+=v[i];
}
}
inline L jdz(L x){
return x>=?x:-x;
}
inline bool judge(int u){
ST(u);
L tmp();
for(int i=;i<=m;i++)
tmp+=(sum[r[i]]-sum[l[i]-])*(quan[r[i]]-quan[l[i]-]);
ans=my_min(ans,jdz(tmp-s));
if(tmp>s)
return true;
return false;
}
inline void ef(int l,int r){
if(l==r)
return;
int mid((l+r)>>);
if(judge(mid))
ef(mid+,r);
else
ef(l,mid);
}
inline int gg(){
freopen("qc.in","r",stdin);
freopen("qc.out","w",stdout);
n=read(),m=read(),s=read();
for(int i=;i<=n;i++){
w[i]=read(),v[i]=read();
edge_mn=my_min(edge_mn,w[i]),edge_mx=my_max(edge_mx,w[i]);
}
for(int i=;i<=m;i++)
l[i]=read(),r[i]=read();
ef(edge_mn,edge_mx+);
printf("%lld",ans);
}
int K(gg());
int main(){;}
[NOIP 2011]聪明的质监员的更多相关文章
- [NOIP 2011] 聪明的质检员
聪明的质检员 描述 小 T 是一名质量监督员,最近负责检验一批矿产的质量.这批矿产共有n个矿石,从1到n逐一编号,每个矿石都有自己的重量wi以及价值vi.检验矿产的流程是:1.给定m个区间[Li,Ri ...
- Codevs 1138 聪明的质监员 2011年NOIP全国联赛提高组
1138 聪明的质监员 2011年NOIP全国联赛提高组 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 黄金 Gold 题目描述 Description 小 T 是一名质量监督员, ...
- 聪明的质监员 2011年NOIP全国联赛提高组(二分+前缀和)
聪明的质监员 2011年NOIP全国联赛提高组 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 黄金 Gold 题目描述 Description 小 T 是一名质量监督员, ...
- NOIP2011提高组 聪明的质监员 -SilverN
题目描述 小T 是一名质量监督员,最近负责检验一批矿产的质量.这批矿产共有 n 个矿石,从 1到n 逐一编号,每个矿石都有自己的重量 wi 以及价值vi .检验矿产的流程是: 1 .给定m 个区间[L ...
- Luogu P1314 聪明的质监员(二分+前缀和)
P1314 聪明的质监员 题意 题目描述 小\(T\)是一名质量监督员,最近负责检验一批矿产的质量.这批矿产共有\(n\)个矿石,从\(1\)到\(n\)逐一编号,每个矿石都有自己的重量\(w_i\) ...
- P1314 聪明的质监员(前缀和+二分)
P1314 聪明的质监员 显然可以二分参数W 统计Y用下前缀和即可. #include<iostream> #include<cstdio> #include<cstri ...
- AC日记——聪明的质监员 洛谷 P1314
聪明的质监员 思路: 二分: 代码: #include <bits/stdc++.h> using namespace std; #define maxn 200005 #define l ...
- 【洛谷P1314】[NOIP2011]聪明的质监员
聪明的质监员 题目链接:https://www.luogu.org/problemnew/show/P1314 Y(W)随W的值增大而减小 二分W的值,找到最小的W使得Y(W)>S: 比较Y(W ...
- 洛谷P1314 聪明的质监员
P1314 聪明的质监员 题目描述 小T 是一名质量监督员,最近负责检验一批矿产的质量.这批矿产共有 n 个矿石,从 1到n 逐一编号,每个矿石都有自己的重量 wi 以及价值vi .检验矿产的流程是: ...
随机推荐
- css3动画小案例
今天与大家来分享一下我做的css3动画案例. 在展示我的案例之前先给大家说说实现这个案例所需要的一些属性. transform 属性允许我们对元素进行旋转.缩放.移动或倾斜. 通过 CSS3 2D转换 ...
- 原生js二级联动
今天说的这个是原生js的二级联动,在空白页面里动态添加并作出相对应的效果. 1 //创建两个下拉列表 select标签 是下拉列表 var sel = document.createElement(& ...
- cygwin vi编辑器左右上下键和删除键乱码错误
安装cygwin后使用其中的vi编辑器时发现上下左右键和删除键乱码,搜索了中文的帮助方案,没有解决,最后搜索了英文的网站,找到了解决方案.参考链接如下:http://superuser.com/que ...
- 【Android Developers Training】 76. 用Wi-Fi创建P2P连接
注:本文翻译自Google官方的Android Developers Training文档,译者技术一般,由于喜爱安卓而产生了翻译的念头,纯属个人兴趣爱好. 原文链接:http://developer ...
- 如何使用apktool反编译,查看androidmanifest的内容
1.下载apktool http://pan.baidu.com/s/1o7Jy090 2.使用方法
- java网络编程之socket
网络编程是什么 网络编程的本质是两个设备之间的数据交换,当然,在计算机网络中,设备主要指计算机.数据传递本身没有多大的难度,不就是把一个设备中的数据发送给两外一个设备,然后接受另外一个设备反馈的数据. ...
- 利用CSS3新特性实现完全兼容的自定义滚动条。
背景:最近项目里面因为统一页面风格,用到了自定义滚动条,在完成之前的那个滚动条的时候,与网上各个滚动条插件实现的方法类似,相当于造了轮子,通过css3的 网上看到的滚动条插件多数是通过监听内容的滚动事 ...
- protobuf转json
方法介绍 protobuf的介绍在这里就不详细介绍了,主要是俺也是刚接触,感兴趣的同学可以去搜索相关博客或者直接去看源码以及google的官方文档(官方文档表示很吃力)或者去这个网站:https:// ...
- KBEngine简单RPG-Demo源码解析(2)
七:服务端资产库文件夹结构http://kbengine.org/cn/docs/concepts/directorys.html看assets, 注意:demo使用的不是默认的assets资产目录, ...
- VMwareTools安装失败提示找不到C headers和gcc目录
在VMware虚拟机上安装好linux系统后,发现往往不能全屏,也不能设置共享文件夹进行文件共享,这时候可以通过安装VMwareTools这个工具来实现文件拖拽.共享和全屏. 安装的过程不再赘述,关键 ...