HDU6333 求组合数前m项的和

@

目录

• 分块
• 莫队

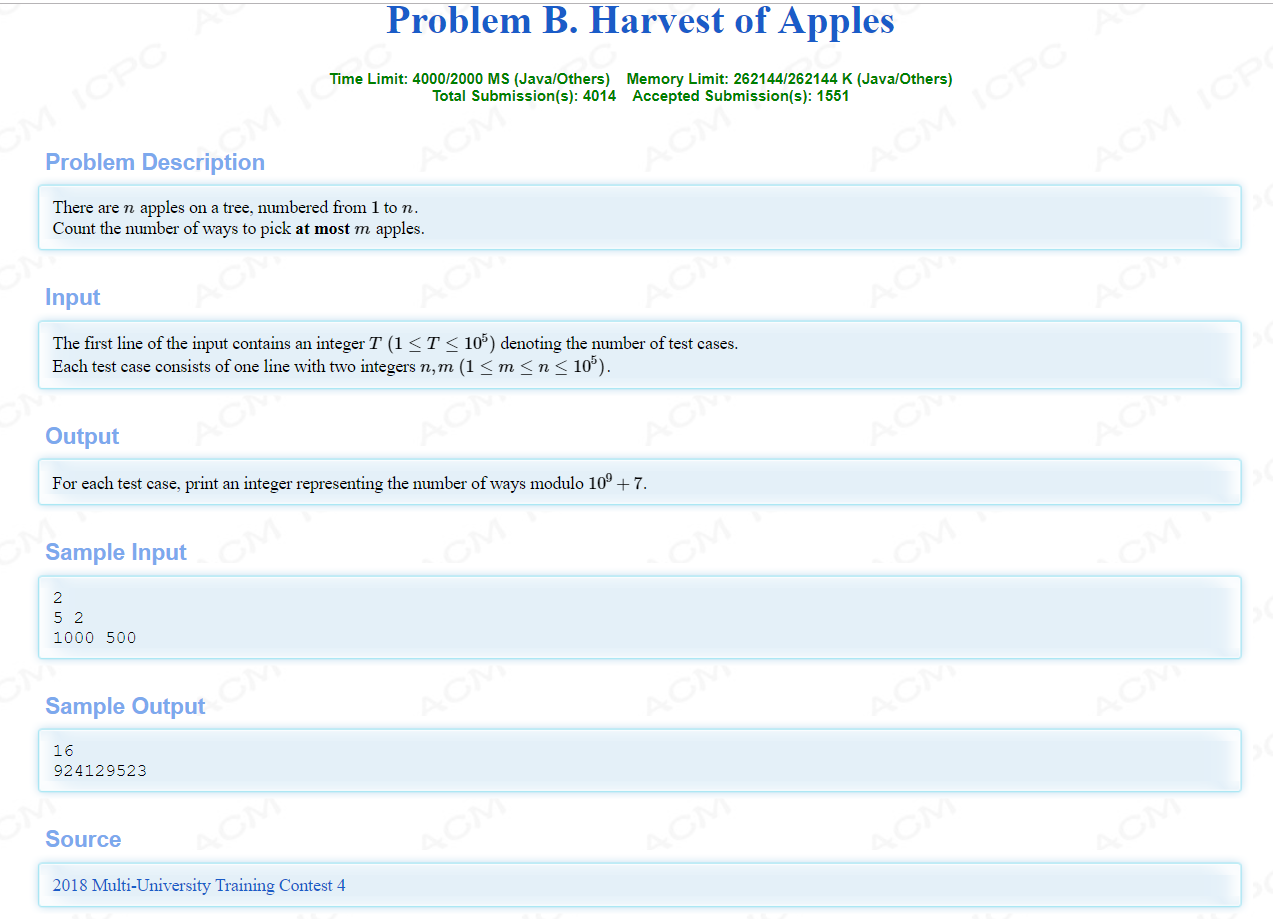
HDU6333：传送门

题意：求组合数前m项的和。

在线分块or离线莫队

分块

重要的一个定理:

\[C_{n}^{m} = 0\;\;m > n
\]

\[C_{n}^{m} = C_{a}^{0}\times C_{b}^{m}+C_{a}^{1}\times C_{b}^{m-1}...+C_{a}^{m}\times C_{b}^{0}\;\;\;a+b = n
\]

\[ans = \sum_{i=0}^m C_n^i=\sum_{i=0}^m(C_a^i\times \sum_{j=0}^{m-i} C_b^j)\;\;a+b=n
\]

然后分块处理，b为整块的大小，块内枚举i求解。

#include<bits/stdc++.h>
#define lson rt<<1
#define rson rt<<1|1
#define all(x) (x).begin(),(x).end()
#define mme(a,b) memset((a),(b),sizeof((a)))
#define fuck(x) cout<<"* "<<x<<"\n"
#define iis std::ios::sync_with_stdio(false)
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
const int MXN = 1e5 + 7;
const int MXE = 1e6 + 7;
const int INF = 0x3f3f3f3f;
const LL MOD = 1e9 + 7;
const LL mod = 1e9 + 7;

int n;
LL l, r;

const int MX = 1e5 + 7;
LL F[MX], invF[MX];
LL ksm(LL a, LL b){
  LL res = 1;
  for(;b;b>>=1,a=a*a%mod){
    if(b&1)res = res * a % mod;
  }
  return res;
}
void init() {
  F[0] = 1;
  for (int i = 1; i < MX; i++) F[i] = F[i - 1] * i % mod;
  invF[MX - 1] = ksm(F[MX - 1], mod - 2);
  for (int i = MX - 2; i >= 0; i--) invF[i] = invF[i + 1] * (i + 1) % mod;
}
LL COMB(int n, int m) {
  if(n == m)return 1;
  if(n < m) return 0;
  return F[n]*invF[m]%mod*invF[n-m]%mod;
}

LL bpre[505][MXN];//bpre[i][j] = sigma(COMB(500*i,k)), k从[0, j]
int blocks = 500;
void yuchuli(){
  for(int i = 1; i < MXN/blocks; ++i){
    for(int j = 0; j < MXN; ++j){
      if(j==0)bpre[i][j] = COMB(blocks*i, j);
      else bpre[i][j] = (bpre[i][j-1] + COMB(blocks*i, j))%MOD;
    }
  }
}

int main(int argc, char const *argv[]){
#ifndef ONLINE_JUDGE
    freopen("E://ADpan//in.in", "r", stdin);
    //freopen("E://ADpan//out.out", "w", stdout);
#endif
  init();
  yuchuli();
  int tim = 1;
  scanf("%d", &tim);
  while(tim--){
    scanf("%lld%lld", &r, &l);
    LL p = r/blocks, re = r - p * blocks, ans = 0;
    LL tmp = min(l, re), limit = p*500;
    //printf("%lld %lld\n", p, re);
    if(p == 0) p = 1, limit = 0;
    for(int i = 0; i <= tmp; ++i){
      ans = (ans + COMB(re, i)*bpre[p][min(l-i, limit)])%MOD;
    }
    printf("%lld\n", ans);
  }
  return 0;
}

莫队

\(S_n^m=\sum C_n^m=Cn^0+Cn^1...+Cn^m\)

\(S_n^{m-1}=\sum C_n^{m-1}=Cn^0+Cn^1...+Cn^{m-1}=S_n^m-C_n^m\)

\(S_n^{m+1}=\sum C_n^{m+1}=Cn^0+Cn^1...+Cn^{m+1}=S_n^m+C_n^{m+1}\)

\(S_{n-1}^m=\sum C_{n-1}^m=C_{n-1}^0+C_{n-1}^1...+C_{n-1}^m=(S_n^m+C_{n-1}^m)\div 2\)

\(S_{n+1}^m=\sum C_{n+1}^m=C_{n+1}^0+C_{n+1}^1...+C_{n+1}^m
=C_{n}^0+(C_{n}^0+C_n^1)+...+(C_n^{m-1}+C_n^m)
=2\times S_n^m-C_n^m\)

若已知S(m,n),则可在O(1)的时间内得到S(m-1,n),S(m+1,n),S(m,n-1),S(m,n+1),莫队即可。

#include<bits/stdc++.h>
#define lson rt<<1
#define rson rt<<1|1
#define fi first
#define se second
#define all(x) (x).begin(),(x).end()
#define lowbit(x) (x&(-(x)))
#define mme(a,b) memset((a),(b),sizeof((a)))
#define test printf("**-**\n")
#define fuck(x) cout<<"* "<<x<<"\n"
#define iis std::ios::sync_with_stdio(false)
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
const int MXN = 2e5 + 7;
const int MXE = 1e6 + 7;
const int INF = 0x3f3f3f3f;
const LL mod = 1e9 + 7;

int n;

const int MX = 1e5 + 5;
LL F[MX], invF[MX];
LL ksm(LL a, LL b){
  LL res = 1;
  for(;b;b>>=1,a=a*a%mod){
    if(b&1)res = res * a % mod;
  }
  return res;
}
void init() {
  F[0] = 1;
  for (int i = 1; i < MX; i++) F[i] = F[i - 1] * i % mod;
  invF[MX - 1] = ksm(F[MX - 1], mod - 2);
  for (int i = MX - 2; i >= 0; --i) invF[i] = invF[i + 1] * (i + 1) % mod;
}
LL COMB(LL n, LL m) {
  if(n == m)return 1;
  if(n < m) return 0;
  return F[n]*invF[m]%mod*invF[n-m]%mod;
}

struct lp{
  int l, r, id;
}cw[MX];
int belong[MX];
LL ans, Ans[MX];
bool cmp(lp &a,lp &b){
  if(belong[a.l]!=belong[b.l])return belong[a.l]<belong[b.l];
  return a.r<b.r;
}

int main(){
#ifndef ONLINE_JUDGE
    freopen("E://ADpan//in.in", "r", stdin);
    //freopen("E://ADpan//out.out", "w", stdout);
#endif
  init();
  scanf("%d", &n);
  int block = sqrt(MX*1.0);
  for(int i = 1; i < MX; ++i)belong[i] = (i-1)/block;
  for(int i = 1; i <= n; ++i){
    scanf("%d%d", &cw[i].r, &cw[i].l);
    cw[i].id = i;
  }
  sort(cw+1,cw+n+1,cmp);
  int L = 1, R = 0;
  ans = 1LL;
  LL two = ksm(2LL, mod-2);
  for(int i = 1; i <= n; ++i){
    while(R<cw[i].r)ans = ((ans * 2LL - COMB(R++, L))%mod+mod)%mod ;
    while(R>cw[i].r)ans = (ans + COMB(--R, L))*two%mod ;
    while(L<cw[i].l)ans = (ans + COMB(R,++L))%mod ;
    while(L>cw[i].l)ans = (ans - COMB(R,L--) + mod)%mod ;
    Ans[cw[i].id] = ans;
  }
  for(int i = 1; i <= n; ++i){
    printf("%lld\n", Ans[i]);
  }
  return 0;
}