【CF1243B2】Character Swap (Hard Version)【思维】

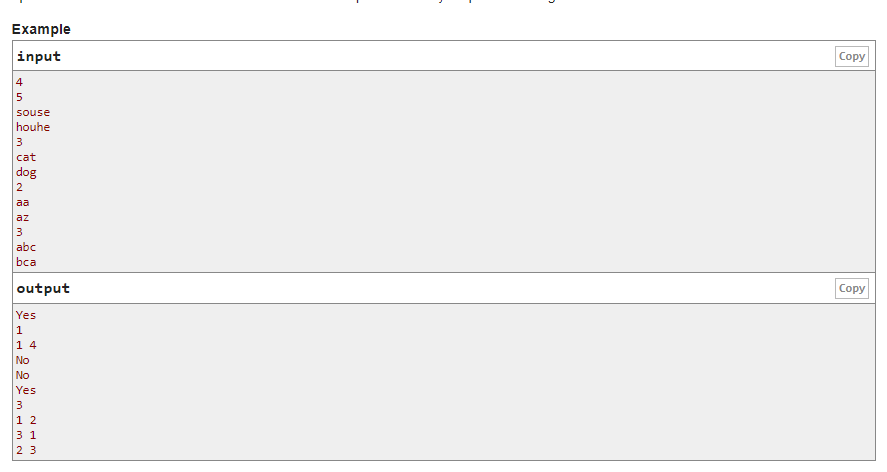
题意：给定两个字符串，问是否存在交换方案使得两个字符串相同，方案为交换次数小于等于2n，且每次只交换s1与s2中的一个字符

题解：考虑从前往后枚举，当第i位不同时，考虑找后边的第j位，若存在这样的第j位，则存在方案

1、存在aj==ai且j>i，那么交换aj,bi

2、存在bj==ai且j>i，那么先交换aj,bj，在交换aj,bi

这样对于每个位置最多两次操作，故若存在方案则一定在2n次内交换完成

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
using namespace std;
int T,n;
char s1[],s2[];
struct node
{
    int a,b;
}mdf[];
int mdfn;
int main()
{
    scanf("%d",&T);
    while(T--)
    {
      scanf("%d%s%s",&n,s1,s2);
      bool fl=;mdfn=;
      for(int i=;i<n;i++)
      {
        if(s1[i]!=s2[i])
        {
          fl=;
          for(int j=i+;j<n;j++)
          {
            if(s1[j]==s1[i])
            {
              mdf[++mdfn]=(node){j,i};
              swap(s1[j],s2[i]);
              fl=;break;
            }
            if(s2[j]==s1[i])
            {
              mdf[++mdfn]=(node){j,j};
              swap(s1[j],s2[j]);
              mdf[++mdfn]=(node){j,i};
              swap(s1[j],s2[i]);
              fl=;break;
            }
          }
          if(!fl){printf("No\n");fl=;break;}
          fl=;
        }
        if(i==n-)fl=;
      }
      if(fl)
      {
        printf("Yes\n%d\n",mdfn);
        for(int i=;i<=mdfn;i++)printf("%d %d\n",mdf[i].a+,mdf[i].b+);
      }
    }
    return ;
}