[洛谷P1864] NOI2009 二叉查找树

问题描述

已知一棵特殊的二叉查找树。根据定义，该二叉查找树中每个结点的数据值都比它左儿子结点的数据值大，而比它右儿子结点的数据值小。

另一方面，这棵查找树中每个结点都有一个权值，每个结点的权值都比它的儿子结点的权值要小。

已知树中所有结点的数据值各不相同；所有结点的权值也各不相同。这时可得出这样一个有趣的结论：如果能够确定树中每个结点的数据值和权值，那么树的形态便可以唯一确定。因为这样的一棵树可以看成是按照权值从小到大顺序插入结点所得到的、按照数据值排序的二叉查找树。

一个结点在树中的深度定义为它到树根的距离加1。因此树的根结点的深度为1。

每个结点除了数据值和权值以外，还有一个访问频度。我们定义一个结点在树中的访问代价为它的访问频度乘以它在树中的深度。整棵树的访问代价定义为所有结点在树中的访问代价之和。

现在给定每个结点的数据值、权值和访问频度，你可以根据需要修改某些结点的权值，但每次修改你会付出K的额外修改代价。你可以把结点的权值改为任何实数，但是修改后所有结点的权值必须仍保持互不相同。现在你要解决的问题是，整棵树的访问代价与额外修改代价的和最小是多少？

输入格式

输入文件中的第一行为两个正整数N，K。其中：N表示结点的个数，K表示每次修改所需的额外修改代价。

接下来的一行为N个非负整数，表示每个结点的数据值。

再接下来的一行为N个非负整数，表示每个结点的权值。

再接下来的一行为N个非负整数，表示每个结点的访问频度。

其中：所有的数据值、权值、访问频度均不超过400000。每两个数之间都有一个空格分隔，且行尾没有空格。

输出格式

输出文件中仅一行为一个数，即你所能得到的整棵树的访问代价与额外修改代价之和的最小值。

样例输入

4 10

1 2 3 4

1 2 3 4

1 2 3 4

样例输出

29

说明

【样例说明】

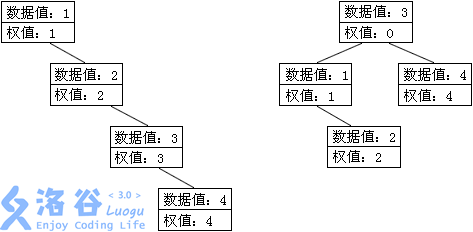
输入的原图是左图，它的访问代价是：1×1+2×2+3×3+4×4=30。

最佳的修改方案是把输入中的第3个结点的权值改成0，得到右图，访问代价是：1×2+2×3+3×1+4×2=19，加上额外修改代价10，一共是29。

【数据规模和约定】

对于40%的数据，满足：N<=30；

对于70%的数据，满足：N<=50；

对于100%的数据，满足：N<=70，1<=K<=30000000。

解析

可以发现，题目所给的意思就是构造了一棵Treap。由于数据值是不会变的，所以根据平衡树的性质，中序遍历也是不会改变的。另外，中序遍历中的一段区间对应着树上的一棵子树，所以，我们可以利用区间DP的思想以及子树根节点的权值是子树中最小的这个性质，得出如下状态：

设\(f[i][j][k]\)表示中序遍历中区间\([i,j]\)得到一棵树且最小权值大于等于k的最小代价。枚举子树的根节点x，如果x的权值小于k，就需要修改权值。我们有如下状态转移方程：

\[f[i][j][k]=min(f[i][x-1][k]+f[x+1][j][k],f[i][x-1][w[x]]+f[x+1][j][w[x]]+K)
\]

同时，因为根节点两边的子树深度均加1，所以需要再加上i到j的频率之和。

另外，每个点的权值可以直接离散化为1到n，不影响答案。

代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define N 72
using namespace std;
struct node{
	int dat,w,f;
}a[N];
int n,m,i,j,k,l,x,val[N],sum[N],f[N][N][N];
int read()
{
	char c=getchar();
	int w=0;
	while(c<'0'||c>'9') c=getchar();
	while(c<='9'&&c>='0'){
		w=w*10+c-'0';
		c=getchar();
	}
	return w;
}
int my_comp(const node &x,const node &y)
{
	return x.dat<y.dat;
}
int main()
{
	n=read();m=read();
	for(i=1;i<=n;i++) a[i].dat=read();
	for(i=1;i<=n;i++){
		a[i].w=read();
		val[i]=a[i].w;
	}
	for(i=1;i<=n;i++) a[i].f=read();
	sort(val+1,val+n+1);
	sort(a+1,a+n+1,my_comp);
	int n1=unique(val+1,val+n+1)-val-1;
	for(i=1;i<=n;i++){
		a[i].w=lower_bound(val+1,val+n1+1,a[i].w)-val;
		sum[i]=sum[i-1]+a[i].f;
	}
	memset(f,0x3f,sizeof(f));
	for(i=1;i<=n+1;i++){
		for(k=1;k<=n;k++) f[i][i-1][k]=0;
	}
	for(l=1;l<=n;l++){
		for(i=1;i+l-1<=n;i++){
			j=i+l-1;
			for(k=1;k<=n;k++){
				for(x=i;x<=j;x++){
					f[i][j][k]=min(f[i][j][k],f[i][x-1][k]+f[x+1][j][k]+m+sum[j]-sum[i-1]);
					if(a[x].w>=k) f[i][j][k]=min(f[i][j][k],f[i][x-1][a[x].w]+f[x+1][j][a[x].w]+sum[j]-sum[i-1]);
				}
			}
		}
	}
	printf("%d\n",f[1][n][1]);
	return 0;
}

反思

并没有注意到这是一个Treap，即使知道了也没有注意到中序遍历不变的性质。所以，多多关注特殊条件特殊性质。