神经网络基础篇：梯度下降法（Gradient Descent）

梯度下降法

梯度下降法可以做什么？

在 测试集上，通过最小化代价函数（成本函数）\(J(w,b)\)来训练的参数\(w\)和\(b\)，

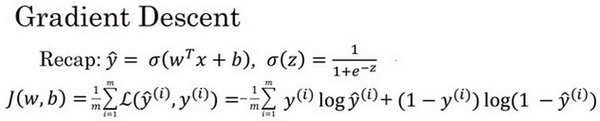
如图，在第二行给出和之前一样的逻辑回归算法的代价函数（成本函数）

梯度下降法的形象化说明

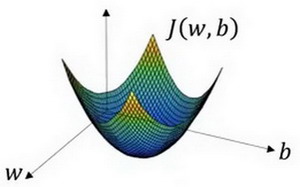
在这个图中，横轴表示 的空间参数\(w\)和\(b\)，在实践中，\(w\)可以是更高的维度，但是为了更好地绘图， 定义\(w\)和\(b\)，都是单一实数，代价函数（成本函数）\(J(w,b)\)是在水平轴\(w\)和\(b\)上的曲面，因此曲面的高度就是\(J(w,b)\)在某一点的函数值。 所做的就是找到使得代价函数（成本函数）\(J(w,b)\)函数值是最小值，对应的参数\(w\)和\(b\)。

如图，代价函数（成本函数）\(J(w,b)\)是一个凸函数(convex function)，像一个大碗一样。

如图，这就与刚才的图有些相反，因为它是非凸的并且有很多不同的局部最小值。由于逻辑回归的代价函数（成本函数）\(J(w,b)\)特性， 必须定义代价函数（成本函数）\(J(w,b)\)为凸函数。

初始化\(w\)和\(b\)，

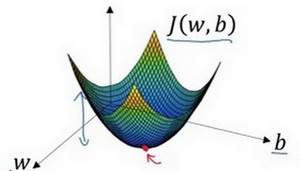
可以用如图那个小红点来初始化参数\(w\)和\(b\)，也可以采用随机初始化的方法，对于逻辑回归几乎所有的初始化方法都有效，因为函数是凸函数，无论在哪里初始化，应该达到同一点或大致相同的点。

以如图的小红点的坐标来初始化参数\(w\)和\(b\)。

2. 朝最陡的下坡方向走一步，不断地迭代

朝最陡的下坡方向走一步，如图，走到了如图中第二个小红点处。

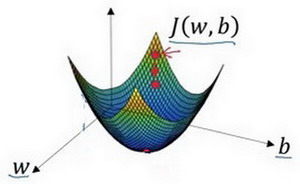
可能停在这里也有可能继续朝最陡的下坡方向再走一步，如图，经过两次迭代走到第三个小红点处。

3.直到走到全局最优解或者接近全局最优解的地方

通过以上的三个步骤 可以找到全局最优解，也就是代价函数（成本函数）\(J(w,b)\)这个凸函数的最小值点。

梯度下降法的细节化说明（仅有一个参数）

假定代价函数（成本函数）\(J(w)\) 只有一个参数\(w\)，即用一维曲线代替多维曲线，这样可以更好画出图像。

迭代就是不断重复做如图的公式:

\(:=\)表示更新参数,

$a $ 表示学习率（learning rate），用来控制步长（step），即向下走一步的长度\(\frac{dJ(w)}{dw}\) 就是函数\(J(w)\)对\(w\) 求导（derivative），在代码中 会使用\(dw\)表示这个结果

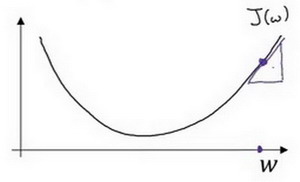
对于导数更加形象化的理解就是斜率（slope），如图该点的导数就是这个点相切于 \(J(w)\)的小三角形的高除宽。假设 以如图点为初始化点，该点处的斜率的符号是正的，即\(\frac{dJ(w)}{dw}>0\)，所以接下来会向左走一步。

梯度下降

整个梯度下降法的迭代过程就是不断地向左走，直至逼近最小值点。

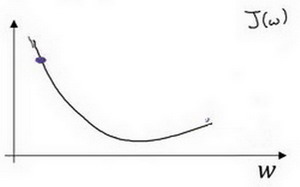
假设 以如图点为初始化点，该点处的斜率的符号是负的，即\(\frac{dJ(w)}{dw}<0\)，所以接下来会向右走一步。

整个梯度下降法的迭代过程就是不断地向右走，即朝着最小值点方向走。

梯度下降法的细节化说明（两个参数）

逻辑回归的代价函数（成本函数）\(J(w,b)\)是含有两个参数的。

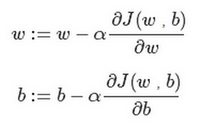
$\partial $ 表示求偏导符号，可以读作round，

\(\frac{\partial J(w,b)}{\partial w}\) 就是函数\(J(w,b)\) 对\(w\) 求偏导，在代码中 会使用\(dw\) 表示这个结果，

\(\frac{\partial J(w,b)}{\partial b}\) 就是函数\(J(w,b)\)对\(b\) 求偏导，在代码中 会使用\(db\) 表示这个结果，

小写字母\(d\) 用在求导数（derivative），即函数只有一个参数，

偏导数符号$\partial $ 用在求偏导（partial derivative），即函数含有两个以上的参数。