oeasy教您玩转vim - 49 - # 命令进阶

​

命令进阶

回忆上节课内容

• 我们上次研究vim的历史
• 为什么会有行编辑器这种东西
• 竟然是当年
• 没有显示器只有纸的时代的无奈之举
• vim进化到今天
• 依然还有好多人使用
• 而且ssh连接的时候直接vim就很方便
• 命令行还有什么好玩的么？

缩进控制

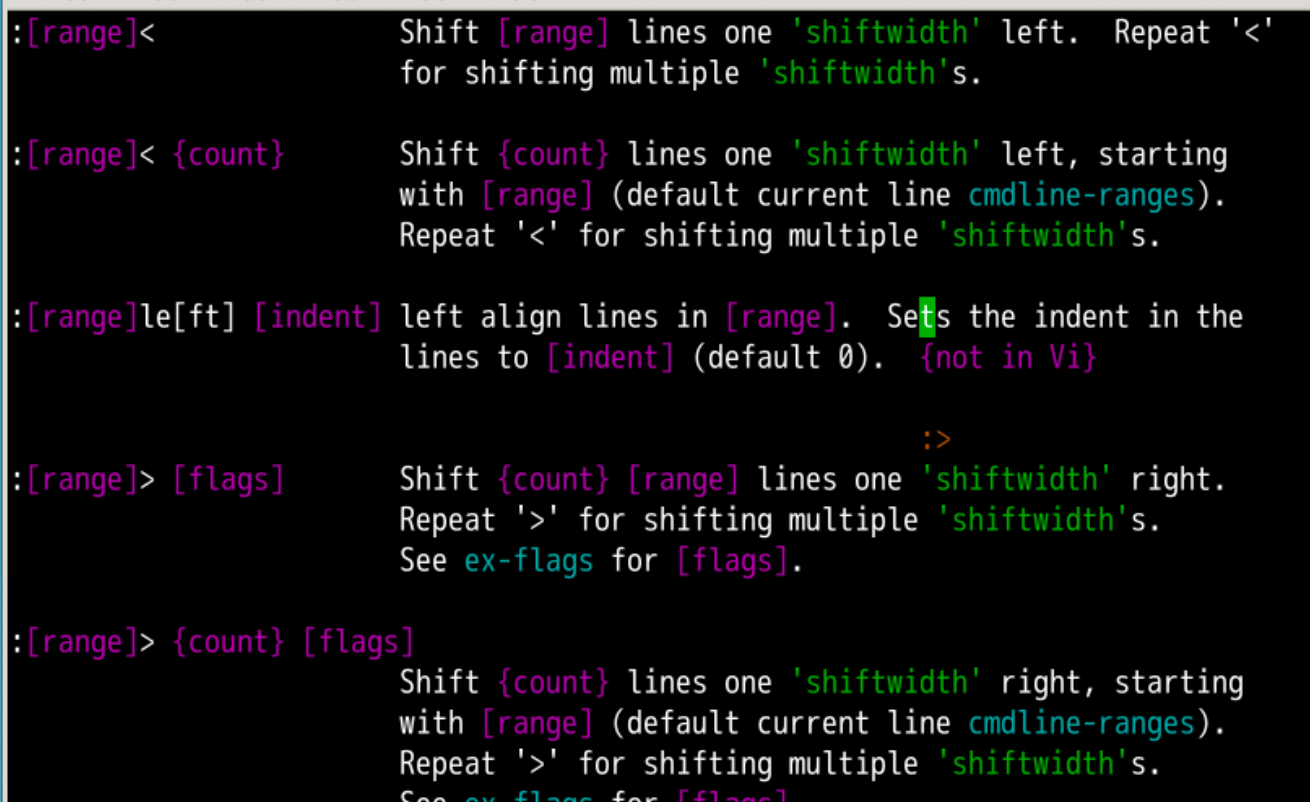
• 我们学习过用<kbd><</kbd><kbd><</kbd>、<kbd>></kbd><kbd>></kbd>控制缩进
  • <kbd><</kbd><kbd><</kbd> 向左一个shiftwidth
  • <kbd>></kbd><kbd>></kbd>向右一个shiftwidth
  • 如果忘了的话,可以:h 'shiftwidth'
• 如果我们想要多行进行控制呢？
  • :20,40>
    • 20-40 行向右一个 shiftwidth
  • :'a,$>
    • a标记 到 结尾 向右一个 shiftwidth
  • %<
    • 所有行向左一个 shiftwidth

​

范围添加分号结尾

• 我们如果想要给从4到10行添加分号结尾，应该如何呢？

• :4,10normal A;

  • 首先是range,先打上:4,10
  • 然后让这个范围内的东西进入 normal 格式再
  • :4,10normal切换为normal模式
  • 打一个空格，后面打上命令A;
    • A是normal模式下的命令在行尾进入插入模式
    • 在最后的位置插入;
  • 整体的命令为:4,10normal A;

• 思考

  • 如果我想在8,15行添加//应该如何做呢？
  • 动手试一试！

• 但是这些都是执行 vim 的内部命令

  • 我想要执行外部命令
  • 比如 shell 中的 ls 可以么？

直接执行外部命令

• 要直接执行外面的命令比如 ls
• 我们在前面加上!就可以
  • 比如:!ls
  • 更复杂一些的
    • !javac oeasy.java
    • !source o2z.sh
    • !python3 %
• 这很方便，直接在vi里面就可以执行命令了
• 而且编译运行能看到报错的结果
  • 直接G跳到出错那行就可以！
• 可以直接修改，很爽！！！
• 超爽！！！
• 不过这一行命令执行完了就没了
• 看不见前面执行的结果了
• 我想一直看见前面的命令和执行结果
• 可以么？

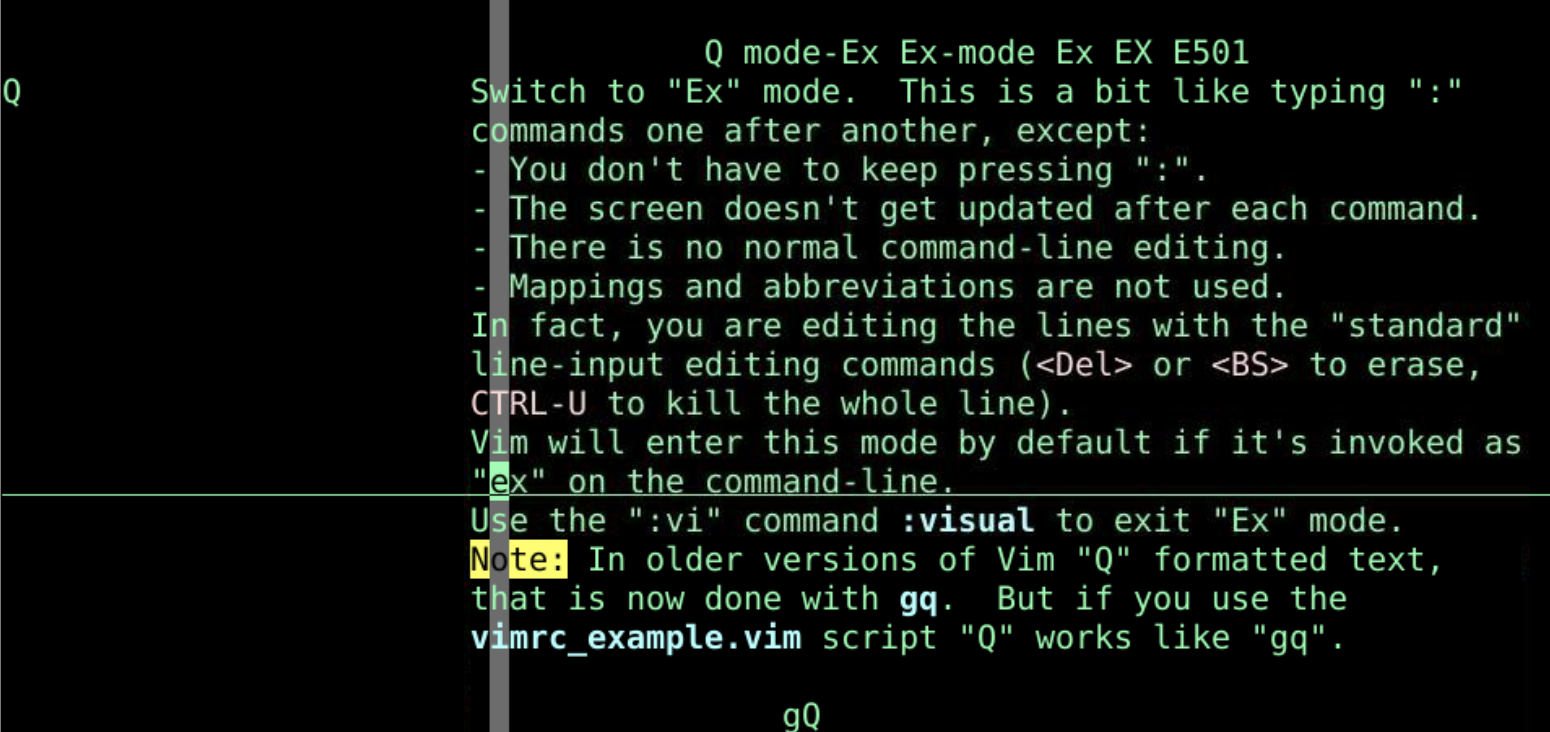
进入命令模式 ex-mode

• 在 Normal 模式下直接按下<kbd>Q</kbd>
• 进入Ex-mode
• 全屏执行命令格式
• 可以执行各种命令行
  • :ls
  • :1,3d
  • :1,7p
  • :visual 退回到正常模式
• 可视化模式 visual 是 vi 名字的来源
• vi 就是ed + 可视化模式 visual

​

• 能直接挂起vim运行命令么？

跳到shell

• 我们知道我们是从 shell 运行 vim 然后进来的
  • 如果我们想退出 vim 的话需要保存并退出:wq
  • 如果我不想保存并退出
  • 就想切到外面
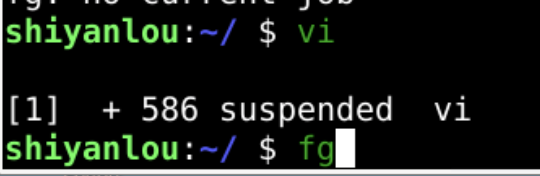
  • 把 vim 整个进程先挂起放到后台
  • 我们就 <kbd>ctrl</kbd>+<kbd>z</kbd>
  • 我们就挂起 vim 切出去了
• 在 shell 运行完命令之后
  • fg就可以把vim切回到前台
  • fg的意思是foreground前台

​

• 但是我们可以直接不挂起 vim 的情况下
• 执行 shell 命令么？

分屏终端 :term

• :term
• 上面切出一个窗口
  • 执行命令
  • exit 退出 shell

​

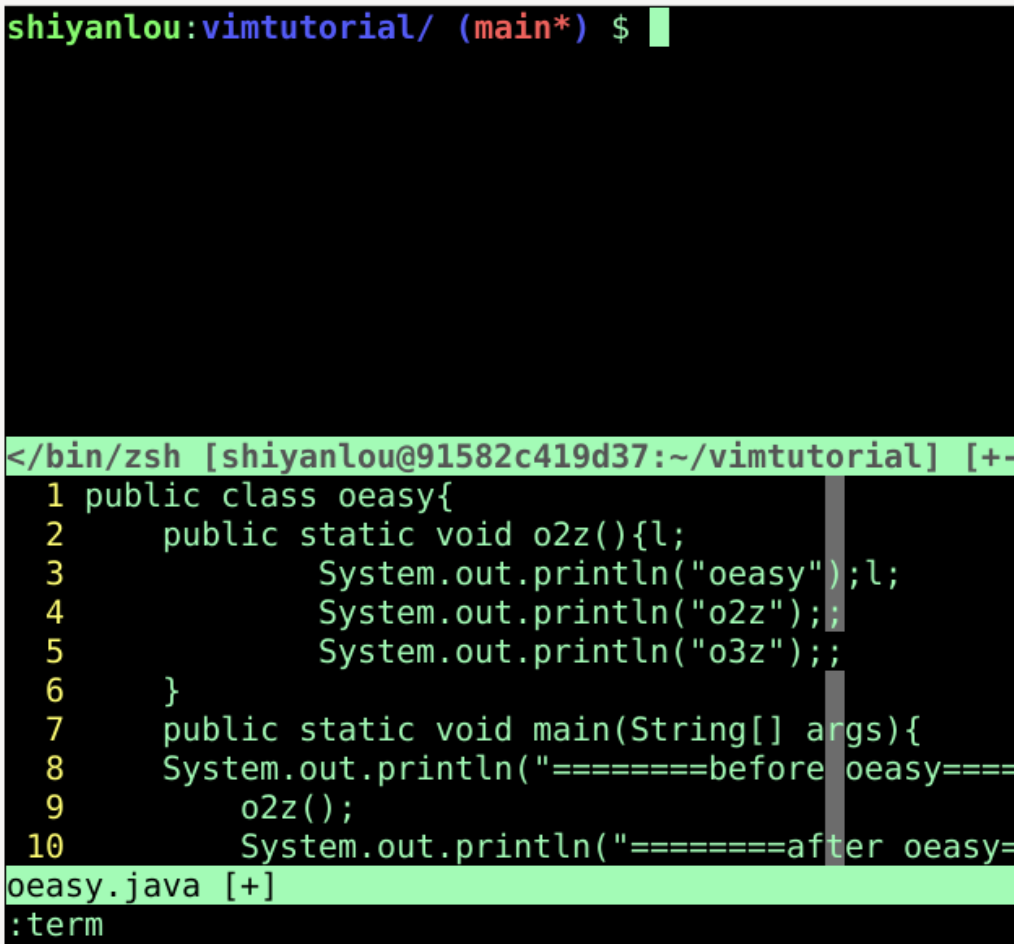
• 上下切换
  • <kbd>ctrl</kbd>+<kbd>w</kbd> <kbd>j</kbd> 切换到下方窗口
  • <kbd>ctrl</kbd>+<kbd>w</kbd> <kbd>k</kbd> 切换到上方窗口
  • 可以切来切去
  • 一边修改一边运行
• 这个 :term 什么意思

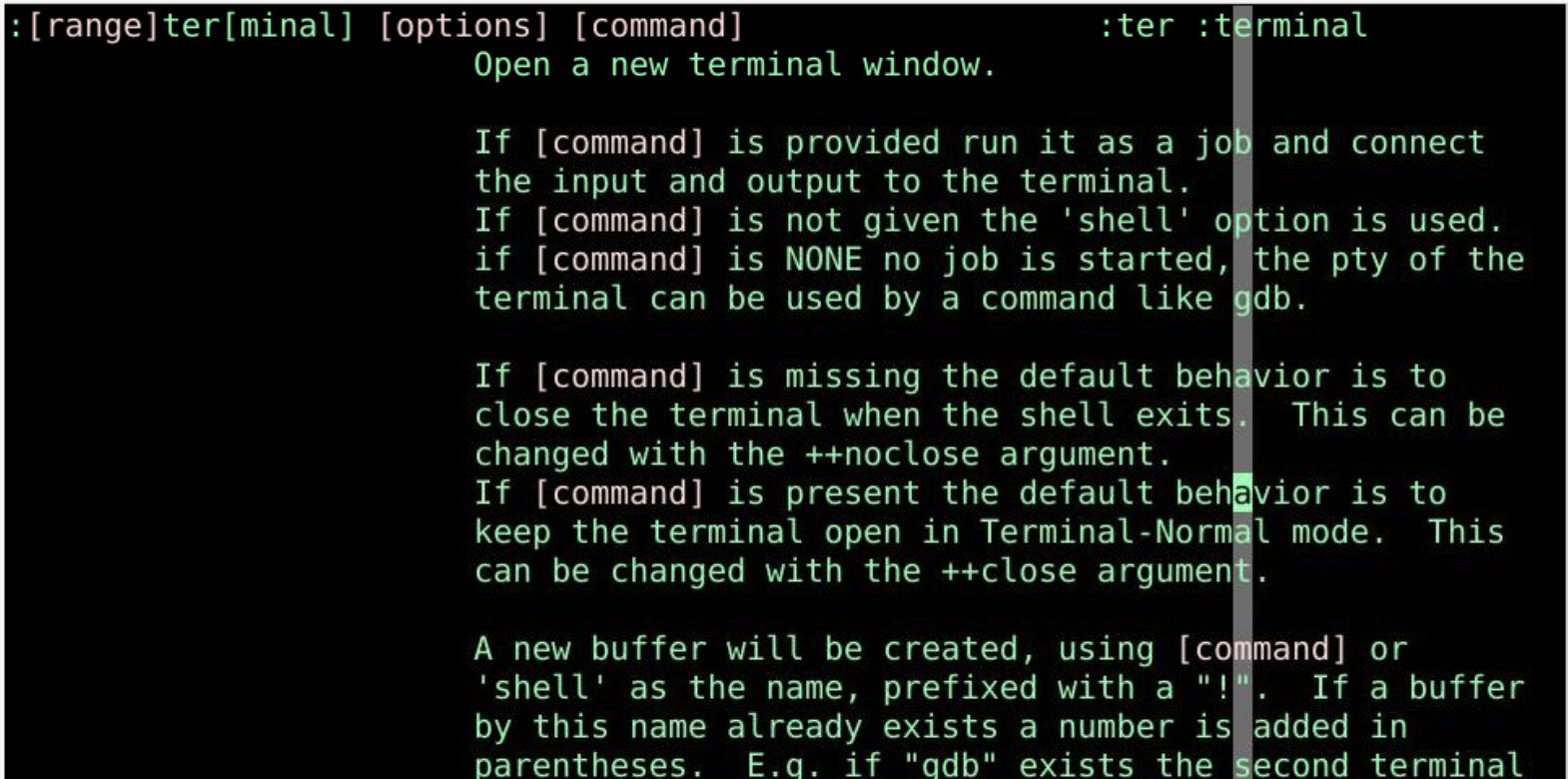
:term 帮助

• 什么不会,:h什么
  • :h :term

​

总结

• 我们这次研究范围命令执行方法
• 批量控制缩进
  • :20,40>
• 批量执行普通模式下的命令
  • :4,10normal A;
• 直接切换到全屏命令模式 ex-mode
  • Q
• 执行外部命令
  • !javac oeasy.java
• 新开一个termianl窗格
  • :term
• 这个方式真的很爽!
  • 在 vi 什么都干了！
• 命令模式本身可以再提高效率吗？
• 下次再说

[Github地址] (https://github.com/overmind1980/oeasyvim)

[Gitee地址] (overmind1980/oeasyvim)

[蓝桥实验楼] (oeasy 教您零基础玩转编辑神器 Vim_Linux - 蓝桥云课)

​