【状态压缩 meet in middle】poj3139Balancing the Scale

数组溢出真是可怕的事情

Description

You are given a strange scale (see the figure below), and you are wondering how to balance this scale. After several attempts, you have discovered the way to balance it — you need to put different numbers on different squares while satisfying the following two equations:

x₁ * 4

x₂ * 3

x₃ * 2

x₄

x₅

x₆ * 2

x₇ * 3

x₈ * 4

y₁ * 4

y₂ * 3

y₃ * 2

y₄

y₅

y₆ * 2

y₇ * 3

y₈ * 4

How many ways can you balance this strange scale with the given numbers?

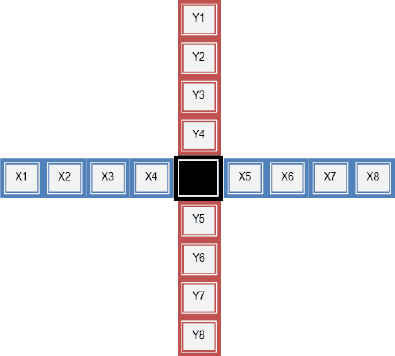
Input

There are multiple test cases in the input file. Each test case consists of 16 distinct numbers in the range [1, 1024] on one separate line. You are allowed to use each number only once.

A line with one single integer 0 indicates the end of input and should not be processed by your program.

Output

For each test case, if it is possible to balance the scale in question, output one number, the number of different ways to balance this scale, in the format as indicated in the sample output. Rotations and reversals of the same arrangement should be counted only once.

Sample Input

87 33 98 83 67 97 44 72 91 78 46 49 64 59 85 88

0

Sample Output

Case 1: 15227223

题目大意

有16个重量互不相同的砝码，问有多少种不同的方案能够使这16个砝码分为两组分别平衡。两个方案不相同当且仅当它们不能够互相旋转或翻转得到。

题目分析

显然是道meet in middle，但是把什么状态折半呢？

$C_{16}^{8}，C_{8}^{4}$

分两次折半搜索，先从16个里取8个，再从选出的8个里取4个。

先用二进制状态压缩，再用$f[i]$表示$i$这个取了8个的状态有多少种合法方案。因为最后的统计是独立的，所以对于总共16个数拆成的状态$i$和状态$j$来说，它们对答案的贡献是$f[i]*f[j]$。

再来考虑如何计算$f[x]$。因为$x$这个状态是选了8个砝码的状态，最普通的计算当然就是$8!$地枚举有多少满足条件。毋庸置疑这里也可以用meet in middle来优化，具体就是用$mp[i][j]$表示$i$这个状态下权值为$j$的方案数。因为8选4之后的4个有$4!$的排列情况，每一种情况的权值都不一样。之后的操作就是比较经典的meet in middle模型了。算出来后再将答案贡献至$f[]$即可。

这是一个正确的算法，但是所要计算的状态数达到了$2*C_{16}^{8}*C_{7}^{4}*4!=21621600$。千万级别的状态数……还是吃不太消。

 #include<bits/stdc++.h>

 int a[],s[],c[];

 int mp[][],f[],bel;

 bool vis[],tk[];

 int scenario;

 long long ans;

 void get(int x, int done, bool opt)

 {

     if (done==){

         register int statu = , tt;

         c[] = ;

         for (int i=; i<x; i++)

             if (tk[i]) statu += <<(i-), c[++c[]] = a[s[i]];

         for (int i=; i<=; i++)

             for (int j=; j<=; j++)

                 if (i!=j)

                     for (int k=; k<=; k++)

                         if (i!=k&&j!=k)

                             for (int l=; l<=; l++)

                                 if (i!=l&&j!=l&&k!=l){

                                     tt = i*c[]+j*c[]+k*c[]+l*c[];

                                     if (!opt)

                                         mp[statu][tt]++;

                                     else f[bel] += mp[-statu][tt];

                                 }

         return;

     }

     if (x > ) return;

     tk[x] = , get(x+, done+, opt);

     tk[x] = , get(x+, done, opt);

 }

 void check()

 {

     memset(mp, , sizeof mp);

     s[] = , bel = ;

     for (int i=; i<=; i++)

         if (vis[i]) s[++s[]] = i, bel += <<(i-);

     get(, , );

     tk[] = ;

     get(, , );

     tk[] = ;

 }

 void dfs(int now, int done, bool opt)

 {

     if (done==){

         if (!opt) check();

         else{

             int status = ;

             for (int i=; i<now; i++)

                 if (vis[i]) status += <<(i-);

             ans += 1ll*f[status]*f[-status];

         }

         return;

     }

     if (now > ) return;

     vis[now] = , dfs(now+, done+, opt);

     vis[now] = , dfs(now+, done, opt);

 }

 int main()

 {

     while (scanf("%d",&a[])&&a[])

     {

         memset(f, , sizeof f);

         for (int i=; i<=; i++) scanf("%d",&a[i]);

         dfs(, , );

         ans = ;

         dfs(, , );

         printf("Case %d: %lld\n",++scenario,ans);

     }

     return ;

 }

高效合并信息

其实上一种做法最关键受限在于选出8个后再选4个。这里每次选4个都是相对独立的操作，而不能共享重复的信息。也就是说，我们其实可以一开始就只考虑选4个，再考虑合并成选8个。

用$f[x]$表示所有权值为$x$的选数方案，于是合并时就可以通过位运算来判断两个状态是否能够合并了。最后统计时也是一样，统计所有选了8个的状态就行了。

第二种相当于是从小信息合并回大信息，不仅时间复杂度优秀，理解和代码复杂度也十分轻松。

注意一下这样子的话，$a[]$数组是要先排序的，否则next_permutation无法遍历全部情况。

 #include<vector>

 #include<cstdio>

 #include<cstring>

 #include<algorithm>

 std::vector<int> f[];

 int bit[],a[],mp[],scenario;

 long long ans;

 bool check(int x)

 {

     bit[] = ;

     for (int i=; i<; i++)

         if (x&(<<i))

             bit[++bit[]] = a[i+];

     return bit[]==;

 }

 int main()

 {

     while (scanf("%d",&a[])&&a[])

     {

         memset(mp, , sizeof mp);

         for (int i=; i<=; i++) scanf("%d",&a[i]);

         std::sort(a+, a+);

         for (int i=; i<=; i++) f[i].clear();

         for (int i=; i<=; i++)

             if (check(i))

                 do{

                     int tt = bit[]*+bit[]*+bit[]*+bit[]*;

                     for (unsigned int j=; j<f[tt].size(); j++)

                         if ((i&f[tt][j])==) mp[i|f[tt][j]]++;

                     f[tt].push_back(i);

                 }while (std::next_permutation(bit+, bit+));

         ans = ;

         for (int i=; i<=; i++)

             ans += 1ll*mp[i]*mp[^i];

         printf("Case %d: %lld\n",++scenario,ans/);

     }

     return ;

 }

真是很奇妙啊……

END