逻辑回归（logic regression）的分类梯度下降

　　首先明白一个概念，什么是逻辑回归；所谓回归就是拟合，说明x是连续的；逻辑呢？就是True和False，也就是二分类；逻辑回归即使就是指对于二分类数据的拟合（划分）。

　　那么什么是模型呢？模型其实就是函数。函数是由三部分组成：自变量，因变量以及参数。

　　此次采用模型是sigmoid函数：

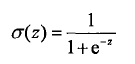
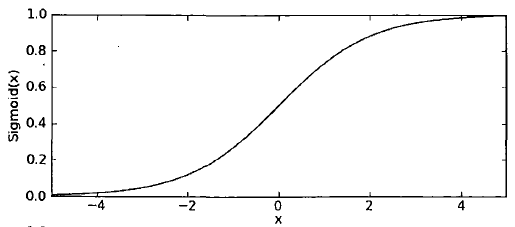
　　sigmoid函数的精妙之处就在于在x=0点出是一个分水岭，x>0y值去1，x<0 y值取0。所以sigmoid函数很像是跃阶函数。

　　z代表什么？则代表分类的数学表达式，是函数的右侧；

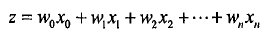
　　那么怎么使用sigmoid阶函数？sigmoid函数目标情况是当传入z，返回值是1或者0；但是实际情况因为参数（w0，w1..wn）都是估计状态，基本都是不为0，1；通过样本分类（0，或者1）和sigmoid值相减，获取一个差量，下面就是调整参数（weight），让数据不断合理；

from numpy import mat
from numpy import shape
from numpy import ones

def gradientAsendent(dataset, labels, time):
　　dataMat=mat(dataset)
　　labelMat=mat(labels).transpose()
　　m,n=shape(dataMat)
　　weights=ones((n,1)) #这个写法（两层括号）是创建一个矩阵
　　alpha=0.001 #学习率rate
　　maxtimes=time
　　for i in range(maxtimes):
　　　　#sigmod函数解决的分类问题，dataMat*weights返回的是一个矩阵，行数=datamat，列数=weights
　　　　h=sigmod(dataMat*weights)
　　　　# 合心意应该error=0，h应该是0,1的数组；但是sigmod返回的分类一定不是正好0,1，而是有差距的
　　　　# 目标就是通过调整系数（weights）来减少减少error的和0的差距，也是让h里面的数据不断的接近0,1
　　　　# 这里注意h是永远绝对值小于等于1的，从sigmond函数图可以看到，值域的取值范围是[0,1]
　　　　error=(labelMat - h)
　　　　# 如果有偏差了，就添加/减小参数值
　　　　weights=weights+alpha*dataMat.transpose()*error
return weights

　　首先要明确，梯度下降算法的目的是求解出系数w1,w2...wn，也就是代码中的weights变量，是一个数组，注意，这里和我们之前的数学里面不是很痒，我们之前是研究系数已知，求解自变量（系数是固定的，自变量是有多个值， 不固定的），但是在机器学习里面，我们是自变量已知，因变量已知，他们就是提供的样本，训练模型的模型的目的求解出系数，所以这个理解思路要调整一下。那么怎么求呢？梯度下降过程是一个试错过程，看一下上述的代码中，初始化的时候所有的参数是1，然后逐渐的调整系数值，每次调整一次系数值就是训练一个新的模型，然后再把样本带进去看看错误率怎么样，基于本次的错误率进行调整系数。

　　注意，敲黑板了，在我们计算错误率的时候，其实就是在使用损失函数，所谓损失函数就是新模型。损失函数一种表达方式是求偏导数（https://www.cnblogs.com/xiashiwendao/p/9470684.html）），另外一种简单的方式本文中提到的直接采用sigmod函数和分类结果做比值；如果是求偏导数的公式如下：

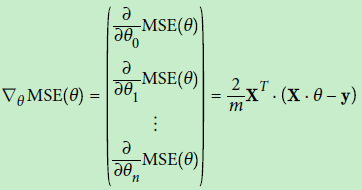
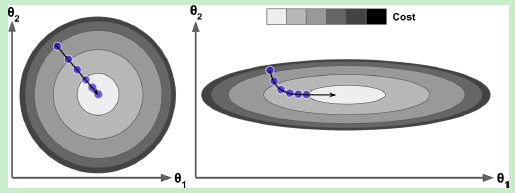
　　在几何图形上，我们可以将求偏导的过程理解为求解切线上面的法线向量（有方向，有大小，大小为步长）；这里就有一个问题，如果是系数取值范围差别比较大，就会导致梯度的下降变慢，为什么呢？因为如下图右图所示，边缘的某点为基础进行梯度下降，最初是的切线是几乎水平，之后，越往里面切线越偏向右边，法线将会逐渐倾向原点，最后到达原点；但是过程相比于左图过程就要漫长的多，如果步长一样的话，那么右图（椭圆）下降速度远小于左图；这个示例说明的两个系数的场景，如果是多个系数，互相影响，将会是在空间上的曲折，对于梯度下降影响将会更大。那么是不是需要做缩放呢？怎么做缩放？这就牵涉到了特征伸缩问题。