Robust Principal Component Analysis?（PCP）

目录

• 引
  • 一些微弱的假设：
• 问题的解决
• 理论
  • 去随机
  • Dual Certificates(对偶保证？)
    • 引理2.4
    • 引理2.5
  • Golfing Scheme
• 数值实验
• 代码

Candes E J, Li X, Ma Y, et al. Robust principal component analysis[J]. Journal of the ACM, 2011, 58(3).

引

这篇文章，讨论的是这样的一个问题：

\[M = L_0 + S_0
\]

有这样的一个矩阵\(M \in \mathbb{R}^{n_1 \times n_2}\)，它由一个低秩的矩阵\(L_0\)和稀疏矩阵\(S_0\)混合而成，那么，能否通过\(M\)将\(L_0\)和\(S_0\)分别重构出来？而且，最关键的是，也是这篇文章的亮点所在：对于\(L_0\)和\(S_0\)仅有一丢丢的微弱的假设。

一些微弱的假设：

关于\(L_0\):

低秩矩阵\(L_0\)不稀疏，这个假设很弱，但有意义。因为如果\(M=e_1e_1^*\)(文章采用\(*\)作为转置符号，这里沿用这种写法)，即只有左上角第一个元素非零，那么这个矩阵如何分解为低秩和稀疏呢，因为压根没法区分。作者引入incoherence condition(不连贯条件？抱歉，不晓得如何翻译)：

假设\(L_0\)的SVD分解为：

\[L_0 = U\Sigma V^*=\sum \limits_{i=1}^r \sigma_i u_i v_i^*
\]

其中\(r = \mathrm{rank}(L_0)\),\(\sigma_i\)为奇异值，并且，\(U = [u_1, \ldots, u_r]\),\(V = [v_1, \ldots, v_r]\)。

incoherence condition:



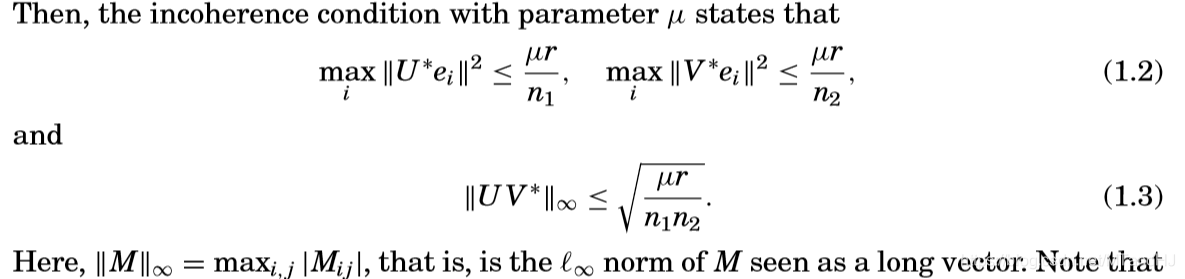
分析这些条件可以发现，\(U,V\)的每一行的模都不能太大，\(UV^*\)的每个元素同样不能太大，所以最后结果\(L_0\)的各个元素的大小会比较均匀，从而保证不稀疏？

关于\(S_0\):

类似地，需要假设\(S_0\)不低秩，论文另辟蹊径，假设\(S_0\)的基为\(m=\mathrm{Card}(S_0)\)，其支撑(support)定义为：

\[\Omega = \{(i,j)| [S_0]_{i,j} \ne 0\}
\]

论文假设\(S_0\)的支撑\(\Omega\)从一个均匀分布采样。即，\(S_0\)不为零的项为\(m\)，从\(n_1\times n_2\)个元素中挑选\(m\)个非零的组合有\(\mathrm{C}_{n_1 \times n_2}^m\)，论文假设每一种组合被采样的概率都是相同的。事实上，关于\(S_0\)元素的符号，论文在后面说明，符号固定或者随机（服从伯努利分布），都能将\(L_0,S_0\)恢复出来。

问题的解决

论文反复强调，多么令人惊讶，多么不可思议，事实上的确如此，上述问题只需求解一个形式非常简单的凸优化问题：



其中\(\|L\|_* = \sum \limits_{i=1}^r \sigma_i(L)\)为其核范数。

论文给出了以下结论：





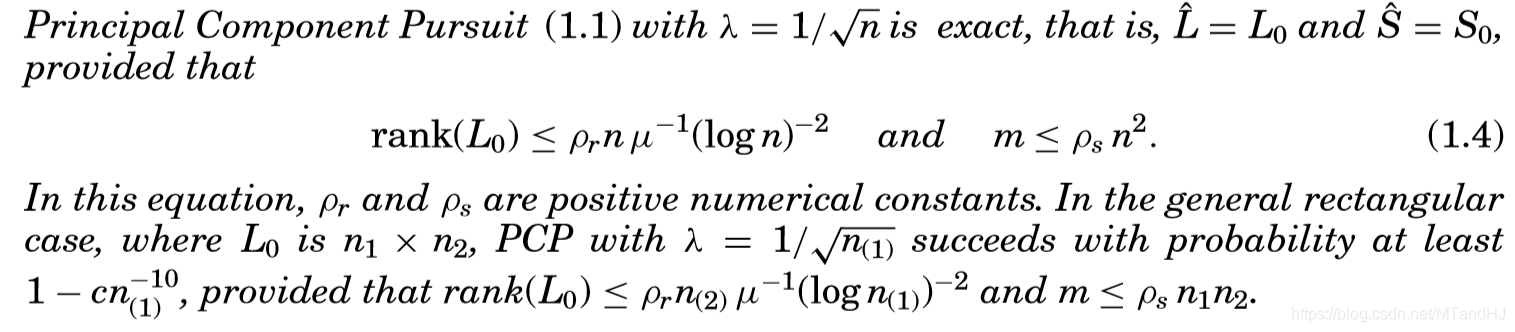
即：令\(n_{(1)}= \max(n_1, n_2), n_{(2)} = \min (n_1, n_2)\)，对于任意矩阵\(M = L_0 + S_0 \in \mathbb{R}^{n_1 \times n_2}\)，只要\(L_0\)和\(S_0\)满足上面提到的假设，那么就存在常数\(c\)使得，PCP的解（即（1.1）的解，且\(\lambda= 1/ \sqrt{n_{(1)}}\)）\(\hat{L}\)和\(\hat{S}\)有\(1-c n_{(1)}^{-10}\)的概率重构\(L_0\)，\(S_0\)，即\(\hat{L}=L_0\)，\(\hat{S}=S_0\)。并且有下列性质被满足\(\mathrm{rank}(L_0) \le \rho_r n_{(2)} \mu^{-1} (\log n_{(1)})^{-2},m \le \rho_s n_1 n_2\)。

这个结果需要说明的几点是，常数\(c\)是根据\(S_0\)的支撑\(\Omega\)决定的（根据后面的理论，实际上是跟\(\|\mathcal{P}_{\Omega} \mathcal{P}_{T}\|\)有关），另外一点是，\(\lambda = 1 / \sqrt{n_{(1)}}\)。是的，论文给出了\(\lambda\)的选择（虽然这个选择不是唯一的），而且，这个值是通过理论分析得到的。

关于问题 (1.1)的求解有很多现成的算法，这篇论文大量篇幅用于证明上述的理论结果，只在最后提到利用ALM（Augmented Largrange multiplier）方法有很多优势，算法如下：



其中\(\mathcal{S}_{\tau}[x] = \mathrm{sgn} (x) \max (|x| - \tau, 0)\), \(\mathcal{D}_{\tau} (X)=U\mathcal{S}_{\tau}(\Sigma)V^*,X=U\Sigma V^*\)。

ALM算法实际上是交替最小化下式：



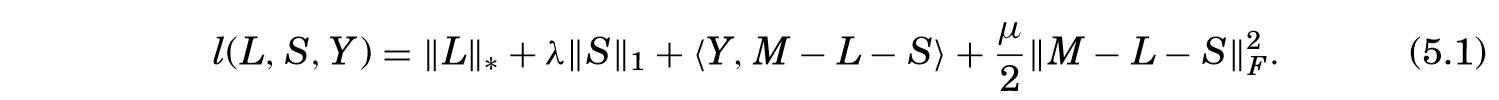
其中\(<A, B>:= \mathrm{Tr(A^TB)}\)。

固定\(L, Y\),实际上就是最小化：

\[\min \quad \lambda \|S\|_1 + <Y, -S> + \frac{\mu}{2}\mathrm{Tr}(S^TS -2S^T(M-L))
\]

其在\(S\)处的导数(虽然有些点并不可导)为：

\[\lambda \mathrm{sgn}(S) - Y + \mu S-\mu(M-L)
\]

实际上，对于每个\(S_{i,j}\)，与其相关的为：

\[a S_{i, j}^2 + b S_{i,j}+c|S_{i,j}|, \alpha > 0
\]

关于最小化这个式子，我们可以得到：

\[S_{i,j}= \left \{ \begin{array}{ll}
-\frac{b+c}{2a} & -\frac{b+c}{2a} \ge 0 \\
-\frac{b-c}{2a} & -\frac{b-c}{2a} \le 0 \\
0 & else
\end{array} \right.
\]

实际上就是\(S_{i,j}= \mathcal{S}_{c/2a}(-b/2a)\)，对\(S\)拆解，容易得到固定\(L,Y\)的条件下，\(S\)的最优解为：

\[\mathcal{S}_{\lambda / \mu}(M-L+\mu^{-1}Y)
\]

当\(S, Y\)固定的时候：

实际上就是最小化下式：

\[\|L\|_* + <Y, -L> + \frac{\mu}{2} \mathrm{Tr(L^TL-L^T(M-S))}
\]

观测其次梯度：

\[UV^*+W-Y+\mu L - \mu(M-S)
\]

其中\(L=U\Sigma V^*，U^*W=0,WV=0,\|W\| \le 1\)，\(\|X\|\)为\(X\)的算子范数。

最小值点应当满足\(0\)为其次梯度，即：

\[L = -\mu^{-1}UV^*-\mu^{-1}W+\mu^{-1}Y + M-S
\]

有解。

令\(A = M-S+\mu^{-1}Y\)

则：

\[L = -\mu^{-1}UV^*-\mu^{-1}W+A \\
\Rightarrow \Sigma=-\mu^{-1}I+U^*AV
\]

假设\(A=U_A\Sigma_A V_A^*\)，那么：

\[\Sigma=-\mu^{-1}I+U^*U_A\Sigma_A V_A^*V
\]

如果我们令\(U=U_A,V=V_A\)，则：

\[\Sigma = \Sigma_A-\mu^{-1}I
\]

但是我们知道，\(\Sigma\)的对角元素必须大于等于0，所以我可以这样构造解：

假设\(\Sigma_A\)的对角元素，即奇异值降序排列\(\sigma_1(A) \ge \sigma_2(A) \ldots \sigma_k(A) \ge \mu^{-1} > \sigma_{k+1}(A) \ge \ldots \ge \sigma_r(A)\)，相对于的向量为\(u_1(A),\ldots,u_r(A)\)和\(v_1{A},\ldots, v_r(A)\)。我们令

\[L=\sum \limits_{i=1}^k (\sigma_i(A)-\mu^{-1})u_i(A)v_i^T(A) \\
W = \sum \limits_{i=k+1}^{r} \mu \sigma_i(A)u_i(A)v_i^T(A)
\]

容易验证\(U^*W=0,WV=0\)，又\(\mu^{-1} > \sigma_i(A), i > k\)，所以\(\mu \sigma_i(A) < 1\)，所以\(\|W\| \le 1\)也满足。同样的，次梯度为0的等式也满足，所以\(L\)就是我们要找到点（因为这个是凸函数，极值点就是最小值点）。

理论

这里只介绍一下论文的证明思路。

符号：

去随机

论文先证明，如果\(S_0\)的符号是随机的（伯努利分布），在这种情况能恢复，那么\(S_0\)的符号即便不随机也能恢复。

Dual Certificates(对偶保证？)

引理2.4

引理2.4告诉我们，只要我们能找到一对\((W, F)\)，满足\(UV^*+W=\lambda(sgn(S_0)+F)\)。\((L_0,S_0)\)是优化问题(1.1)的唯一解。但是不够，因为这个条件太强了，\(W, F\)的构造是困难的。

引理2.5

进一步改进，有了引理2.5。



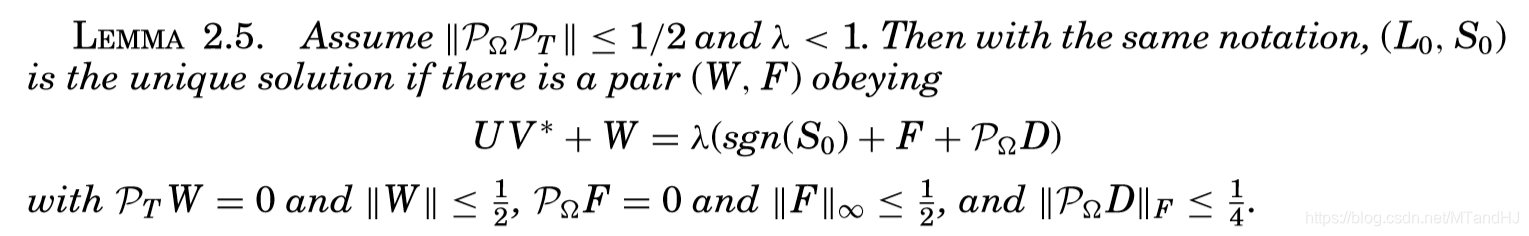
引理2.5的意义在哪呢？它意味着，我们只要找到一个\(W\)，满足：



那么，\((L_0,S_0)\)就是问题\((1.1)\)的最优解，而且是唯一的。

Golfing Scheme

接下来，作者介绍一种机制来构造\(W\)，并且证明这种证明能够大概率保证\(W\)能够满足上述的对偶条件。作者将\(W = W^L + W^S\)分解成俩部分，俩部分用不同的方式构造：



接下的引理和推论，总结起来便是最后的证明：









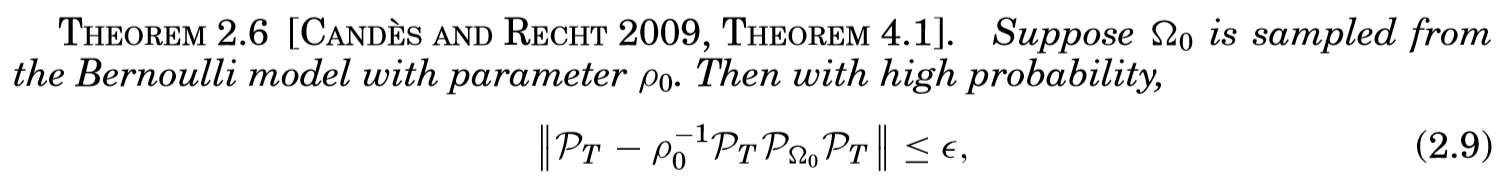
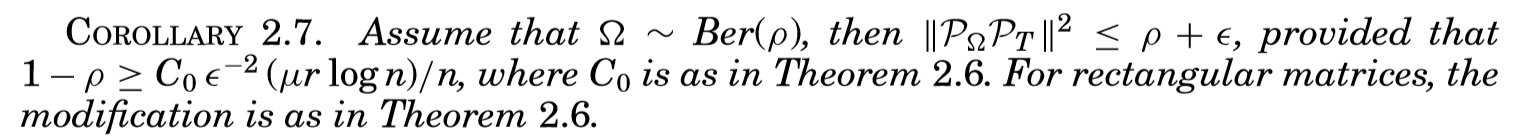
通过引理2.8和2.9，再利用范数的三角不等式，容易验证\(W = W^L+W^S\)满足对偶条件。

最后提一下，定理的概率体现在哪里，在对偶条件的引理中，有这么一个假设\(\|\mathcal{P}_{\Omega}\mathcal{P}_T\| \le 1\)和\(\|\mathcal{P}_{\Omega}\mathcal{P}_T\| \le 1/2\)，这些条件并不一定成立，根据\(\Omega\)的采样，成立的大概率的。

数值实验

按照论文里，普通的人工生成矩阵，实验下来和论文的无异。也的确，\(S_0\)的规模大小（每个元素的大小）对能否恢复几乎没有影响，有影响的是\(S_0\)的稀疏度。实验下来，稀疏度越高（0基越小），恢复的越好，而且差距蛮大的。

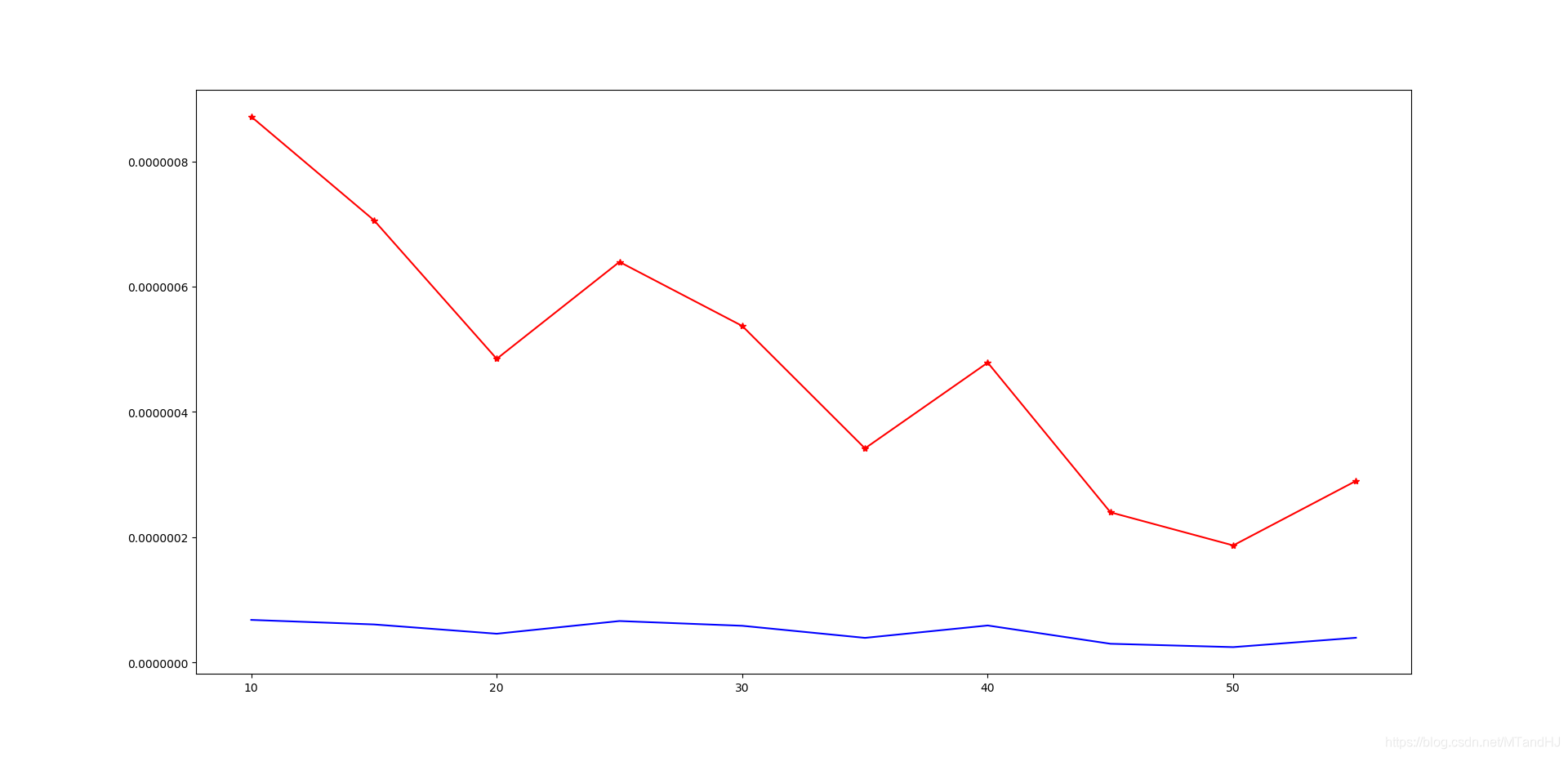
我们的实验，\(L = XY\)，其中\(X,Y \in \mathbb{R}^{500 \times 25}\)依标准正态分布生成的，\(S_0\)是每个元素有\(\rho\)的概率为\(100\)，\(\rho\)的概率为\(-1\)，\(1-2\rho\)的概率为0。\(\rho\)我们选了\(1/10, 1/15, \ldots, 1/55\)。

下面的图，红色表示\(\|\hat{L}-L_0\|_F/\|L_0\|_F\)，蓝色表示\(\|\hat{S}-S_0\|_F/\|S_0\|_F\)。因为每种情况我只做了一次实验，所以结果有起伏，但是趋势是在的。

比较有意思的是图片的拆解，我在马路上拍了31张照片，按照论文的解释，通过将照片拉成向量，再混合成一个矩阵\(M\)，然后通过优化问题解出\(\hat{L}\)和\(\hat{S}\)，那么\(\hat{L}\)的行向量（我做实验的时候是将一个照片作为一个行向量，论文里的是列向量）重新展成图片应该是类似背景的东西，而\(\hat{S}\)中对应的行向量应该是原先图片中会动的东西。

照片我进行了压缩(\(416 \times 233\))和灰度处理，处理\(M\)用了1412次迭代，时间大概15分钟？比我预想的快多了。

我挑选其中比较混乱的图（就是车比较多的）：

第一组：

M:



L:



S:



第二组：

M:

L:



S:



第三组：

M:

L:



S:

比较遗憾的是，\(\hat{S}\)中都出现了面包车，我以为面包车会没有的，结果还是出现了。

代码

"""
Robust Principal Component Analysis?
"""

import numpy as np

class RobustPCA:

    def __init__(self, M, delta=1e-7):
        self.__M = np.array(M, dtype=float)
        self.__n1, self.__n2 = M.shape
        self.S = np.zeros((self.__n1, self.__n2), dtype=float)
        self.Y = np.zeros((self.__n1, self.__n2), dtype=float)
        self.L = np.zeros((self.__n1, self.__n2), dtype=float)
        self.mu = self.__n1 * self.__n2 / (4 * self.norm_l1)
        self.lam = 1 / np.sqrt(max(self.__n1, self.__n2))
        self.delta = delta

    @property
    def norm_l1(self):
        """返回M的l1范数"""
        return np.sum(np.abs(self.__M))

    @property
    def stoprule(self):
        """停止准则"""
        A = (self.__M - self.L - self.S) ** 2
        sum_A = np.sqrt(np.sum(A))
        bound = np.sqrt(np.sum(self.__M ** 2))
        if sum_A <= self.delta * bound:
            return True
        else:
            return False
    def squeeze(self, A, c):
        """压缩"""
        if c <= 0:
            return A
        B1 = np.where(np.abs(A) < c)
        B2 = np.where(A >= c)
        B3 = np.where(A <= -c)
        A[B1] = [0.] * len(B1[0])
        A[B2] = A[B2] - c
        A[B3] = A[B3] + c
        return A

    def newsvd(self, A):
        def sqrt(l):
            newl = []
            for i in range(len(l)):
                if l[i] > 0:
                    newl.append(np.sqrt(l[i]))
                else:
                    break
            return np.array(newl)
        m, n = A.shape
        if m < n:
            C = A @ A.T
            l, u = np.linalg.eig(C)
            s = sqrt(l)
            length = len(s)
            u = u[:, :length]
            D_inverse = np.diag(1 / s)
            vh = D_inverse @ u.T @ A
            return u, s, vh
        else:
            C = A.T @ A
            l, v = np.linalg.eig(C)
            s = sqrt(l)
            length = len(s)
            v = v[:, :length]
            D_inverse = np.diag(1 / s)
            u = A @ v @ D_inverse
            return u, s, v.T

    def update_L(self):
        """更新L"""
        A = self.__M - self.S + self.Y / self.mu
        u, s, vh = np.linalg.svd(A) #or self.newsvd(A)
        s = self.squeeze(s, 1 / self.mu)
        s = s[np.where(s > 0)]
        length = len(s)
        if length is 0:
            self.L = np.zeros((self.__n1, self.__n2), dtype=float)
        elif length is 1:
            self.L = np.outer(u[:, 0] * s[0], vh[0])
        else:
            self.L = u[:, :length] * s @ vh[:length]

    def update_S(self):
        """更新S"""
        A = self.__M - self.L + self.Y / self.mu
        self.S = self.squeeze(A, self.lam / self.mu)

    def update_Y(self):
        """更新Y"""
        A = self.__M - self.L - self.S
        self.Y = self.Y + self.mu * A

    def process(self):
        count = 0
        while not (self.stoprule):
            count += 1
            assert count < 10000, "something wrong..."
            self.update_L()
            self.update_S()
            self.update_Y()
        print(count)

注意到，我自己写了一个newsvd的方法，这是因为，在处理图片的时候，用numpy的np.linalg.svd会报memoryerror，所以就自己简单调整了一下。