HDU 2865 Birthday Toy [Polya 矩阵乘法]

传送门

题意：

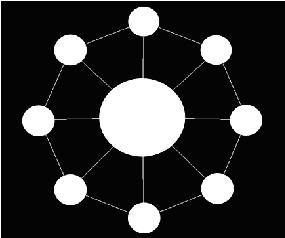
相邻珠子不能相同，旋转等价。$n$个珠子$k$中颜色，求方案数

---

首先中间珠子$k$种选择，$k--$
如果没有相邻不同的限制，就和$POJ\ 2154$一样了
$|C(f)|=k^{\#(f)}$
但是有了相邻不同的限制，每种循环的颜色就不能任意选择了
旋转等价循环个数是$gcd(n,i)$，同一个循环的元素相差$i$步
容易得到只要满足长度$gcd(n,i)$的一段相邻颜色不同整个环就不同了，因为这样的一段正好每个循环有一个元素
考虑$DP$，$f[i]$表示$i$个元素组成的环染色方案数
$f[i]=(k-2)*f[i-1]+(k-1)*f[i-2]$
因为这时候$i-1$是可以和$1$相同的，那样$i$有$k-1$种选择，所以加上后面的一块
显然可以用矩阵快速幂
计算的时候使用和和$POJ\ 2154$同样的技巧
最后的式子为：
$\frac{k}{n}\sum\limits_{d \mid n}{f(d)*\phi(\frac{n}{d})},\ d \neq 1$

注意：$Candy?$把矩阵的构造函数里加上了每个矩阵都初始化为单位矩阵，认为这样就不用在做矩阵快速幂前初始化了。

然后就被坑惨了......矩阵乘法里还需要零矩阵啊啊啊啊啊啊啊 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=1e5+,P=1e9+;
typedef long long ll;
inline int read(){
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-; c=getchar();}
    while(c>=''&&c<=''){x=x*+c-''; c=getchar();}
    return x*f;
}
int n;
ll k;
int p[N];
bool notp[N];
void sieve(int n){
    for(int i=;i<=n;i++){
        if(!notp[i]) p[++p[]]=i;
        for(int j=;j<=p[]&&i*p[j]<=n;j++){
            notp[i*p[j]]=;
            if(i%p[j]==) break;
        }
    }
}
inline int phi(int n){
    int re=n,m=sqrt(n);
    for(int i=;i<=p[]&&p[i]<=m&&p[i]<=n;i++) if(n%p[i]==){
        re=re/p[i]*(p[i]-);
        while(n%p[i]==) n/=p[i];
    }
    if(n>) re=re/n*(n-);
    return re%P;
}
struct Matrix{
    ll a[][];
    ll* operator [](int x){return a[x];}
    Matrix(){a[][]=a[][]=a[][]=a[][]=;}
    void ini(){a[][]=a[][]=;}
}a,b;
Matrix operator *(Matrix a,Matrix b){
    Matrix c;
    for(int k=;k<;k++)
        for(int i=;i<;i++) if(a[i][k])
            for(int j=;j<;j++) if(b[k][j])
                (c[i][j]+=a[i][k]*b[k][j])%=P;
    return c;
}
Matrix operator ^(Matrix a,int b){
    Matrix re;re.ini();
    for(;b;b>>=,a=a*a)
        if(b&) re=re*a;
    return re;
}
ll F[];
ll f(int x){
    if(x<=) return F[x];
    Matrix re=a^(x-);
    re=re*b;
    return re[][];
}
inline void mod(int &x){if(x>=P) x-=P;}
inline ll Pow(ll a,int b){
    ll re=;
    for(;b;b>>=,a=a*a%P)
        if(b&) re=re*a%P;
    return re;
}
inline ll Inv(ll a){return Pow(a,P-);}
void solve(){
    int m=sqrt(n),ans=;
    for(int i=;i<=m;i++) if(n%i==){
        if(i!=) mod(ans+= f(i)*phi(n/i)%P);
        if(i*i!=n) mod(ans+= f(n/i)*phi(i)%P);
    }
    printf("%lld\n",ans*Inv(n)%P*(k+)%P);
}
int main(){
    freopen("in","r",stdin);
    sieve();
    while(scanf("%d%lld",&n,&k)!=EOF){
        k--;
        F[]=k;F[]=k*(k-)%P;F[]=k*(k-)%P*(k-)%P;
        a[][]=k-; a[][]=k-;
        a[][]=;     a[][]=;
        b[][]=F[];b[][]=;
        b[][]=F[];b[][]=;
        solve();
    }
}