[MCSM]随机搜索和EM算法

1. 概述

本节将介绍两类问题的不同解决方案。其一是通过随机的搜索算法对某一函数的取值进行比较，求取最大/最小值的过程；其二则和积分类似，是使得某一函数被最优化，这一部分内容的代表算法是EM算法。（书中章节名称为Optimization）

2. 随机搜索

对于优化，一本很有名的书是Stephen Boyd 的凸优化（Convex Optimization）。但看过的人可能思维会受到一点限制。最简单、最基本的求最大/最小值的算法，除了直接求解，就是把所有的可能值枚举出来，然后求最大/最小就可以了，而不是凸优化里面的下降方法。

当然，一个基本的条件是定义域有界，这样即使定义域连续，我们也可以求到足够近似的解。譬如如果要求解函数

在[0,1]之间的最大值，采用搜索算法可得到如下结果

MATLAB 代码

a = rand(,);

a = sort(a);

b = (cos(*a) + sin(*a)).^;

a = (:)./;

c = (cos(*a) + sin(*a)).^;

subplot(,,);

plot(a,c);xlabel('Function');

subplot(,,);

plot(a,b,'.','MarkerSize',4.5);xlabel('Evaluation');

max(b)

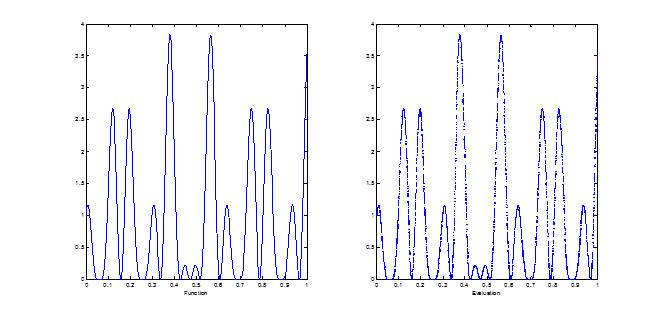
但问题是这种方法很有可能要花费很多资源，但即便如此，在低维的很多问题下，速度还是可以接受的。在这一方法中我没没有利用任何的需要求解函数的特征（除了映射关系），从这一角度上来看，搜索方法还是有很大改进的余地的。

3. 梯度方法

参考凸优化中的基本算法——梯度下降，我们构造了一序列进行搜索，序列满足

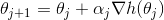
更一般的情况下，我们需要对上面的式子加上一些扰动。这是因为函数或是解空间不是那么规则（我的理解是凸性），此时算法变成了（Rubinstein）

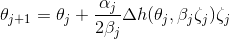
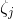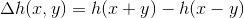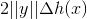其中，服从均匀分布且范数为1，是的逼近。

4. 模拟退火   

另一类算法是模拟退火算法，这一算法最初被应用在有限集合最小化准则函数下（Metropolis et al），但后来也被用在最优化连续集合上。这一算法引入了温度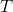来改变搜索的尺度。算法可描述如下

1. 按照指定分布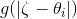仿真产生；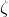

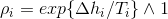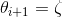2. 依概率接受，否则保持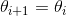

3. 更新

同第一节中的例子，MATLAB代码

% 定义域[,]

for m = :

    x = zeros(,);

    y = (cos(*x) + sin(*x)).^;

    for k = :

        T_t = /log(k);

        a = max(,x(k-)-0.5);

        b = min(,x(k-)+0.5);

        x(k) = a+(b-a)*rand();

        y(k) = (cos(*x(k)) + sin(*x(k))).^;

        if(y(k) < y(k-))

            if(rand()>exp((y(k)-y(k-))/T_t))

                x(k) = x(k-);

                y(k) = (cos(*x(k)) + sin(*x(k))).^;

            end

        end

    end

    subplot(,,m);

    plot(x,y,'Marker','.');

end

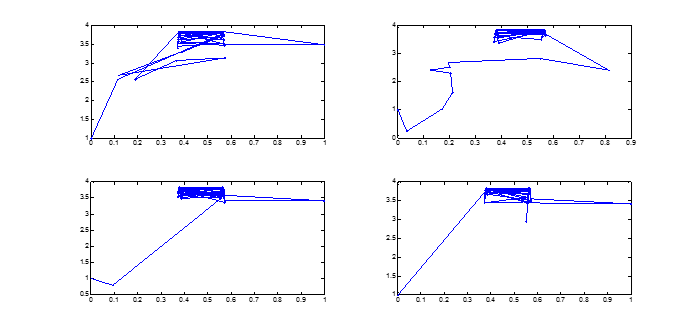
    由于函数在[0,1]之间有两个最大值，最后模拟退火算法在两个值之间来回抖动。

5. Prior Feedback

没看懂（p169）

6. 随机近似（Stochastic Approximation）

We next turn to methods that work more directly with the objective function rather than being concerned with fast explorations of the space.

意思就是实际上之前的搜索算法解决的实际上是（以最大化为例）

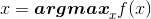
也就是在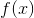的定义域上搜索最大值的过程。然而这里回到更本质的问题上去计算函数的最大/最小值在什么地方取得。

7. Missing Data Models（缺失数据模型）

文中提到这些近似方法多用在缺失数据模型中，此处先简要介绍缺失数据模型。数据的缺失往往会使得观测模型变得很复杂，譬如说Censored Data Model（观测范围有限，小于或大于某常数的观测值缺失了）以及混合模型（mixture models）。以下举例说明：

Censored Data Model Likewood：

假设我们观测到独立同分布的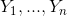服从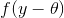，假设前m没有被限制幅度，后n-m个被限制为a（最大值），那么似然函数可以表示为

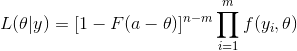
如果假设我们得到了最后n-m的准确值，那么完整的似然函数应该是

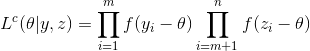
同时有

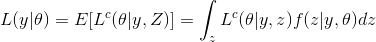
这几个式子告诉我们，观测量似然函数和完整似然函数之间的关系，这一点在下一节将会用到。

8. EM算法

文中的EM算法介绍实在是晦涩难懂，而且各种似然函数和条件概率写法没有区别……

可以参考 http://en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm或是 JerryLead的文章（EM算法）The EM Algorithm。（这两个的思想不一样）

下面是书本上的表示，感兴趣的还是去看WIKI上的吧，这个表示写得真的乱七八糟

---

从缺失数据模型考虑，对于缺失数据而言，条件概率可以表示为

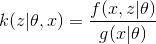
完整似然函数和观测数据似然函数之间的关系可以表示为（对于任意的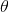都成立）注意这里的L都代表似然函数。

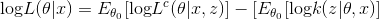
为了最大化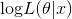，我们先只关注右侧式子的第一项。

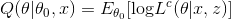
我们之后最大化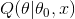，如果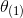使得式子取值最大，那么更新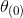，也就是说

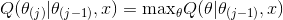
此处EM算法具体表现为

1. E-step 计算（注意此处求解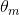最后只是代入求条件概率去了，所以最后还是会有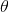出现）

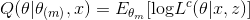
2. 最大化

---

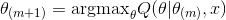
EM算法的思想在于，由于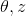都是未知的，此时不好求解，但是一旦其中一个固定，求另一个以最大化似然函数就变得简单了，而迭代进行这个过程，会得到最优值，有点类似坐标下降法。（EM算法是一种贪婪的算法，所以可能会收敛到局部最优）

对于EM算法收敛到最优值，可以证明，序列满足

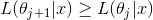
单且仅当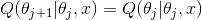时等号成立。这是因为（定义）

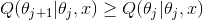
和（Jensen不等式）

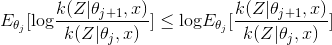
9. 其他