Solution -「AGC 004E」「AT 2045」Salvage Robots

\(\mathcal{Description}\)

  Link.

  有一个 \(n\times m\) 的网格。每个格子要么是空的，要么有一个机器人，要么是一个出口（仅有一个）。每次可以命令所有机器人向上下左右中的某个方向同时移动一格，如果某个机器人超出了棋盘的边界就会死亡。如果它到了出口的位置就会获救。求获救机器人的最大值。

  \(n,m\le100\)。

\(\mathcal{Solution}\)

  换系，以任一机器人为参考系，使出口成为唯一的动点。设 \(f(u,d,l,r)\) 表示出口向上最多移 \(u\) 格，向下最多移 \(d\) 格，向左最多移 \(l\) 格，向右最多移 \(r\) 格，最多能救到的机器人数量。

  故 \(f(0,0,0,0)=0\) 为初始状态，考虑向上下左右四个方向转移。但需要注意，出口的移动会导致网格外层的一些机器人死亡。如图：

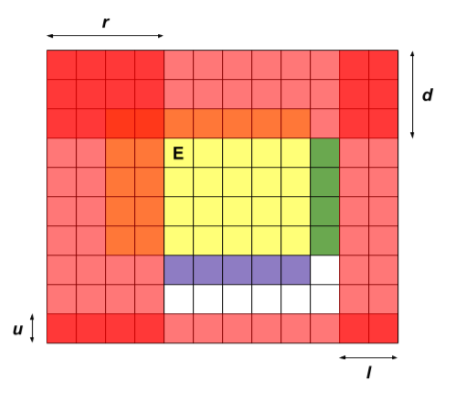
  以图为例，有 \(f(u,d+1,l,r)=f(u,d,l,r)+\operatorname{count}(purple)\)，\(f(u,d,l,r+1)=f(u,d,l,r)+\operatorname{count}(green)\)。

  总之，亿 点 细 节 即可。

\(\mathcal{Code}\)

  用 short 卡空间不香嘛 qwq~

#include <cstdio>

#define int short
#define int32 signed

const int MAXN = 100;
int n, m, er, ec, srow[MAXN + 5][MAXN + 5], scol[MAXN + 5][MAXN + 5];
int f[MAXN + 1][MAXN + 1][MAXN + 1][MAXN + 1];

inline void chkmax ( int& a, const int b ) { if ( a < b ) a = b; }
inline int max_ ( const int a, const int b ) { return a < b ? b : a; }
inline int min_ ( const int a, const int b ) { return a < b ? a : b; }

inline int rsum ( const int row, const int l, const int r ) {
	return l > r ? 0 : srow[row][r] - srow[row][l - 1];
}

inline int csum ( const int col, const int u, const int d ) {
	return u > d ? 0 : scol[col][d] - scol[col][u - 1];
}

int32 main () {
	int32 tn, tm; char str[MAXN + 5];
	scanf ( "%d %d", &tn, &tm ), n = tn, m = tm;
	for ( int i = 1; i <= n; ++ i ) {
		scanf ( "%s", str + 1 );
		for ( int j = 1; j <= m; ++ j ) {
			if ( str[j] == 'E' ) er = i, ec = j;
			srow[i][j] = srow[i][j - 1] + ( str[j] == 'o' );
			scol[j][i] = scol[j][i - 1] + ( str[j] == 'o' );
		}
	}
	int umx = er - 1, dmx = n - er, lmx = ec - 1, rmx = m - ec;
	for ( int u = 0; u <= umx; ++ u ) {
		for ( int d = 0; d <= dmx; ++ d ) {
			for ( int l = 0; l <= lmx; ++ l ) {
				for ( int r = 0, cur, aliveL, aliveR, aliveU, aliveD; r <= rmx; ++ r ) {
					cur = f[u][d][l][r];
					aliveL = max_ ( r + 1, ec - l ), aliveR = min_ ( m - l, ec + r );
					chkmax ( f[u + 1][d][l][r],
						cur + ( er - u - 1 >= d + 1 ? rsum ( er - u - 1, aliveL, aliveR ) : 0 ) );
					chkmax ( f[u][d + 1][l][r],
						cur + ( er + d + 1 <= n - u ? rsum ( er + d + 1, aliveL, aliveR ) : 0 ) );

					aliveU = max_ ( d + 1, er - u ), aliveD = min_ ( n - u, er + d );
					chkmax ( f[u][d][l + 1][r],
						cur + ( ec - l - 1 >= r + 1 ? csum ( ec - l - 1, aliveU, aliveD ) : 0 ) );
					chkmax ( f[u][d][l][r + 1],
						cur + ( ec + r + 1 <= m - l ? csum ( ec + r + 1, aliveU, aliveD ) : 0 ) );
				}
			}
		}
	}
	int32 ans = f[umx][dmx][lmx][rmx];
	printf ( "%d\n", ans );
	return 0;
}