是一个五元组

M=(S,∑,f,S0,F)

其中

S：有穷状态集

∑：输入字母表(有穷)

f：状态转换函数。f(S,a)=S'

是单值部分映射，每个状态面临一个输入符号时，转入的后继状态是确定的。

S0∈S：唯一初态

F∈S：终态集(可空)

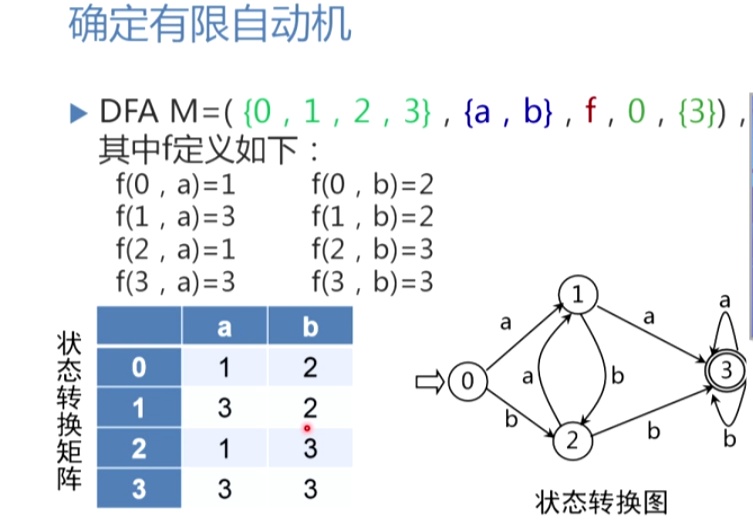
编译原理-确定有穷自动机(deterministic finite automata ，DFA)的更多相关文章

  1. 编译原理-非确定有穷自动机(nondeterministic finite automata,NFA)

    是一个五元组,M=(S,∑,f,S0,F) S:有穷状态集 ∑:输入字母表(有穷) f:f(S,α)=S' 表示从一个状态S出发,识别了一个字α后,可以到达S'这个状态集合之间的某一个状态(可能的后继 ...

  2. 编译原理实验 NFA子集法构造DFA,DFA的识别 c++11实现

    实验内容 将非确定性有限状态自动机通过子集法构造确定性有限状态自动机. 实验步骤 1,读入NFA状态.注意最后需要设置终止状态. 2,初始态取空,构造DFA的l0状态,将l0加入未标记状态队列que ...

  3. 编译原理：正规式转变成DFA算法

    //将正规式转变成NFApackage hjzgg.formal_ceremony_to_dfa; import java.util.ArrayList; class Edge{ public int ...

  4. Compiler Theory(编译原理)、词法/语法/AST/中间代码优化在Webshell检测上的应用

    catalog . 引论 . 构建一个编译器的相关科学 . 程序设计语言基础 . 一个简单的语法制导翻译器 . 简单表达式的翻译器(源代码示例) . 词法分析 . 生成中间代码 . 词法分析器的实现 ...

  5. 编译原理_P1004

    龙书相关知识点总结 //*************************引论***********************************// 1. 编译器(compiler):从一中语言( ...

  6. 编译原理-词法分析05-正则表达式到DFA-01

    编译原理-词法分析05-正则表达式到DFA 要经历 正则表达式 --> NFA --> DFA 的过程. 0. 术语 Thompson构造Thompson Construction 利用ε ...

  7. 正则表达式引擎的构建——基于编译原理DFA（龙书第三章）——3 计算4个函数

    整个引擎代码在github上,地址为:https://github.com/sun2043430/RegularExpression_Engine.git nullable, firstpos, la ...

  8. 编译原理-NFA构造DFA

    本题摘自北邮的编译原理与技术. 首先,根据此图构造状态转换表 表中第一列第一行表示从第一个符号B通过任意个空转换能到达的节点,Ia表示由此行的状态数组({B,5,1}可以看作0状态)经过一个a可以到达 ...

  9. 《编译原理》构造与正规式 (0|1)*01 等价的 DFA - 例题解析

    <编译原理>构造与正规式 (0|1)*01 等价的 DFA - 例题解析 解题步骤: NFA 状态转换图 子集法 DFA 的状态转换矩阵 DFA 的状态转图 解: 已给正规式:(0|1)* ...

随机推荐

  1. 前端小白的学习之路html与css的较量【一】

    html和css的较量 web结构的组成 html标签规则 快速生成一个html html的基本结构 标签的关系 标签 标题标签 段落 图片 超链接 a 属性 a标签里面的值 字符实体 新增的标签 1 ...

  2. 截取字符串长度，超出部分用省略号代替 PHP

    function subText($text, $length){ if (mb_strlen($text, 'utf8') > $length) { return mb_substr($tex ...

  3. No input file specified.问题的解决

    问题描述:apache配置网站出现问题"No input file specified." 解决1: 打开.htaccess 在RewriteRule 后面的index.php教程 ...

  4. chemfig化学式转换为pdf

    SMILES 与 chemfig 针对化学分子结构,可以用SMILES (用ASCII字符串明确描述分子结构的规范)来定义. SMILES(Simplified molecular input lin ...

  5. algorithm库介绍之---- stable_sort()方法 与 sort()方法 .

    文章转载自:http://www.cnblogs.com/ffhajbq/archive/2012/07/24/2607476.html 关于stable_sort()和sort()的区别: 你发现有 ...

  6. CSS3过渡应用

    小米图标转换 transition:需要过渡的属性 花费时间 (运动曲线 何时开始): Tips: 1.第二个属性值必须跟上单位(s) 2.谁要过渡给谁加 图标转换最终效果:当鼠标划过图标时,缓慢转换 ...

  7. 普里姆（Prim）算法

    概览 普里姆算法(Prim算法),图论中的一种算法,可在加权连通图(即"带权图")里搜索最小生成树.即此算法搜索到的边(Edge)子集所构成的树中,不但包括了连通图里的所有顶点(V ...

  8. [Java] Spring 示例

    (一)IoC/DI 功能 配置解析:将配置文件解析为BeanDefinition结构,便于BeansFactory创建对象 对象创建:BeansFactory 根据配置文件通过反射创建对象,所有类对象 ...

  9. 在python的class中的,self到底是什么？

    答案:self可以理解为一个字典变量,内部存的就是对象的数据属性.如:{'name':'zhang','age':'18'}就是这些. 注意只有数据属性,并没有创建新的类的方法.  类-----> ...

  10. Tomcat修改jdk版本

    tomcat修改jdk版本 修改tomcat bin目录下的catalina.sh和setclasspath.sh文件,添加以下内容 export JAVA_HOME=/home/nodemanage ...