charles抓取https设置
第一步:打开charles,查看电脑ip,手机设置代理(需要手机和电脑在同一网络)
手机下载证书不要用自带的下,会失败
1、查看电脑ip

2、手机设置代理,修改网络,保存
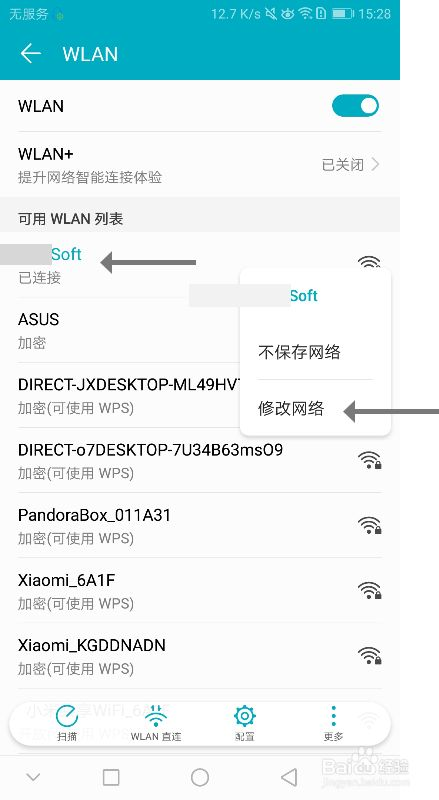
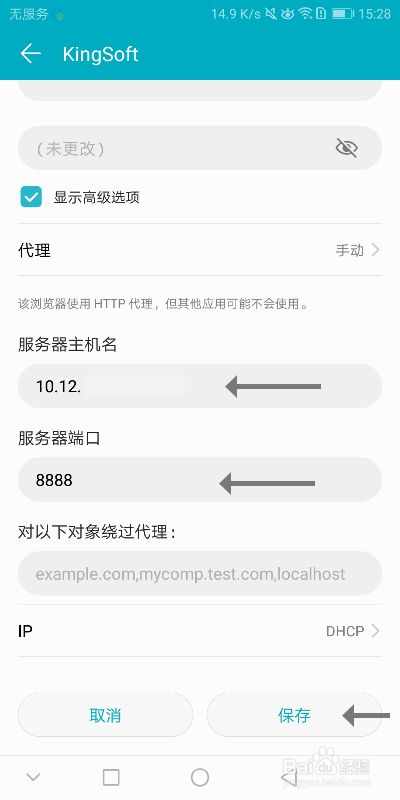
3、手机访问"看图片,发不出连接"安装证书
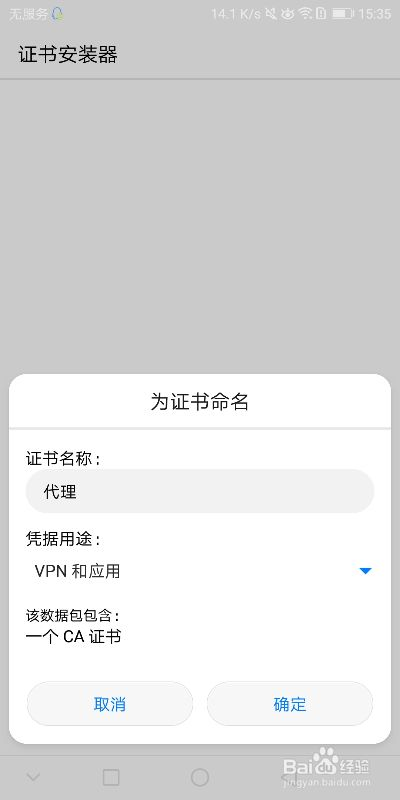
4、电脑端在charles里面设置(重要)
设置两个*就可以了
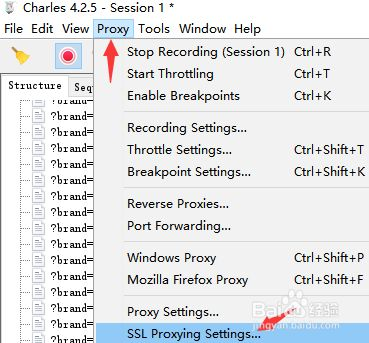
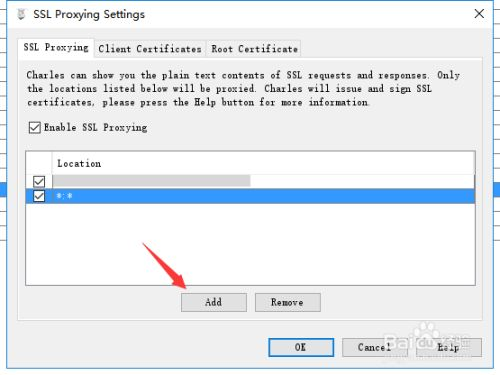
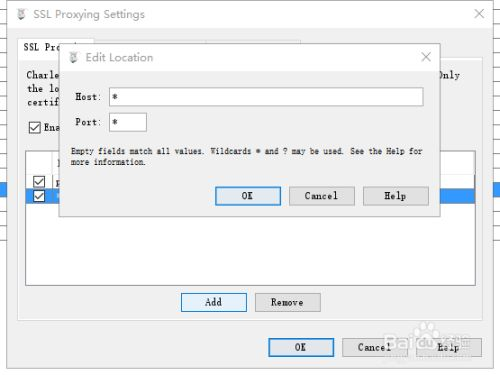
5、完成,可以看到https的请求了

注意事项:
第四步很重要
charles抓取https设置的更多相关文章
- charles抓取HTTPS设置,详细踩坑版
写这篇文章的背景就是,每次我在一台新电脑上用charles抓包时,总是因为各种原因无法抓到https请求,每个百度出来的回答又不是那么详细,需要通过几篇回答才能解决过程中的各种问题,所以把自己的安装经 ...
- charles抓取https请求包
说明: 用charles抓取https请求,会出现SSL Proxying disabled in Proxy Settings这样的提示,如下图.要通过charles抓取数据,还需要进行一些简单的设 ...
- 手机通过Charles抓取https包
因为fiddler不能在mac上使用,而Charles是跨平台的,可以在mac上使用,所以需要了解一下Charles的使用 安装破解版Charles 下载破解版包,先启动一次未破解版的Ch ...
- 对比使用Charles和Fiddler两个工具及利用Charles抓取https数据(App)
对比使用Charles和Fiddler两个工具及利用Charles抓取https数据(App) 实验目的:对比使用Charles和Fiddler两个工具 实验对象:车易通App,易销通App 实验结果 ...
- Fiddler抓取https设置及其原理
iddler抓取https设置及其原理 2018-02-02 目录 1 HTTPS握手过程2 Fiddler抓取HTTPS过程3 Fiddler抓取HTTPS设置参考 数字签名是什么? 1 HTTPS ...
- fiddler软件测试——Fiddler抓取https设置详解(图文)(摘抄)
随笔- 8 文章- 0 评论- 0 fiddler软件测试——Fiddler抓取https设置详解(图文) 强烈推荐(原创亲测)!!!Fiddler抓取https设置详解(图文)转 本文主要说 ...
- fiddler软件测试——Fiddler抓取https设置详解(图文)
强烈推荐(原创亲测)!!!Fiddler抓取https设置详解(图文)转 本文主要说明了自己在设置fiddler抓取https过程中所遇到的问题及解决步骤,特别是fiddler在设置证书的环节遇到的各 ...
- 爬虫之Fiddler抓取HTTPS设置
Fiddler抓取HTTPS设置 启动Fiddler,打开菜单栏中的 Tools > Telerik Fiddler Options,打开“Fiddler Options”对话框. 对Fiddl ...
- fiddler 4 抓取 https 设置
Fiddler抓取https 设置 1.打开fiddler,点击工具栏中的Tools—>Options,点击Actions,选择最后一项,Reset All certificates,然后关闭, ...
随机推荐
- Netty 框架学习 —— 基于 Netty 的 HTTP/HTTPS 应用程序
通过 SSL/TLS 保护应用程序 SSL 和 TLS 安全协议层叠在其他协议之上,用以实现数据安全.为了支持 SSL/TLS,Java 提供了 javax.net.ssl 包,它的 SSLConte ...
- 第三方API对接如何设计接口认证?
一.前言 在与第三方系统做接口对接时,往往需要考虑接口的安全性问题,本文主要分享几个常见的系统之间做接口对接时的认证方案. 二.认证方案 例如订单下单后通过 延时任务 对接 物流系统 这种 异步 的场 ...
- excel函数提取身份证出生日期,分离日期时间的日期和时间
1.提取身份证出生日期 =1*TEXT(MID(H13,7,8),"0-00-00")用MID函数提取表示日期的位数,再用text函数转换为格式1998-6-21格式的文本,再通过 ...
- excel匹配函数vlookup和lookup
1.vlookup(查找的条件,查找的区域,满足查找条件后需要返回的值在选中的查找区域的第几列,精确匹配还是近似匹配(精确匹配为0或False表示,反之为1或True)) =VLOOKUP(J2,$G ...
- 1、mysql基础入门(1)
1.mysql基础入门: 1.1.数据库介绍:
- POJ 2663 Tri Tiling dp 画图找规律
状态:d[i]代表n=i时的方案数. 状态转移方程:d[i]=d[i-2]+2*(d[i-2]+d[i-4]+-+d[0]) i只会为偶数,奇数情况不存在,d[0]=1 找状态转移方程的时候画图更好理 ...
- AcWing 1127. 香甜的黄油
农夫John发现了做出全威斯康辛州最甜的黄油的方法:糖. 把糖放在一片牧场上,他知道 N 只奶牛会过来舔它,这样就能做出能卖好价钱的超甜黄油. 当然,他将付出额外的费用在奶牛上. 农夫John很狡猾, ...
- 重新整理 .net core 实践篇————缓存相关[四十二]
前言 简单整理一下缓存. 正文 缓存是什么? 缓存是计算结果的"临时"存储和重复使用 缓存本质是用空间换取时间 缓存的场景: 计算结果,如:反射对象缓存 请求结果,如:DNS 缓存 ...
- Raspberry Pi:树莓派开发板配置USB启动系统
准备材料 树莓派4B U盘 TF卡 树莓派基础镜像2020-08-20稳定版(这个系统是必须的并拷录在TF卡) Kali树莓派系统(这个是我想要学习的系统,大家可以准备自己的系统,拷录在U盘的) SD ...
- 微信app支付,完整流程,完整代码 (转)
微信app支付流程 需要的配置参数 private function wechat($body,$indent_id,$cou,$user_id,$total_fee,$ip,$domain,$non ...
