【C/C++】习题3-2 分子量/算法竞赛入门经典/字符串

给出一种物质的分子式，求分子量。只包含4种原子，分别为C,H,O,N。

【知识点】

1.ASCII码

【阿拉伯数字】48~57

【大写字母】65~90

【小写字母】97~122

2.输入循环到n-1的原因

因为我用的结束输入是enter+ctrlz+enter的结束方法，但是读入字符的话，会多一个enter。

->直接scanf("%s")就不会多一个enter，但是因为数组长度是n，而数组下标是从0开始，所以实际坐标是0到n-1.

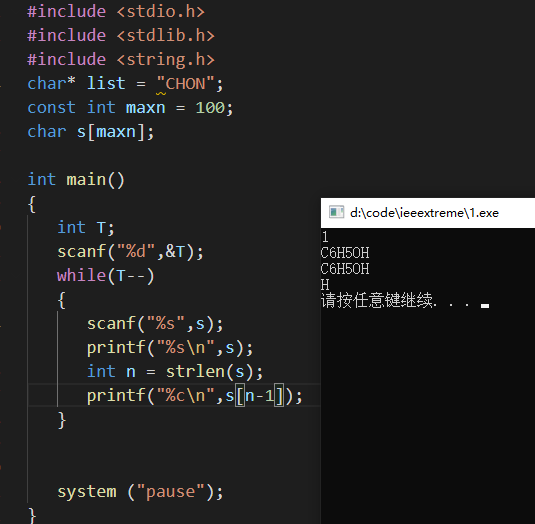
【代码】

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
const char* list = "CHON";
float weight[] = {12.01, 1.008, 16.00, 14.01};
const int maxn = 100;
char s[maxn];

int get_loc(char a)
{
   for (int i = 0; i < 4; i++)
   {
      if(a == list[i]) return i;
   }
   return -1;
}

int main()
{
   int T;
   float sum = 0.0;
   scanf("%d",&T);
   while(T--)
   {
      scanf("%s",s);
      printf("%s\n",s);
      int n = strlen(s);
      int loc;
      //printf("%c\n",s[n-1]);
      if( s[n-1]>=48 && s[n-1]<=57 ) //最后一位是数字
      {
         for(int i = 0; i < n ; i++) //可以读到最后一位
         {
            if (s[i] >= 65 && s[i]<= 90)
            {
               loc = get_loc(s[i]);
               if (s[i + 1] >= 65 && s[i + 1]<= 90) //如果下一位是字母
               {
                  sum += weight[loc];
               }
               else //如果下一位是数字
               {
                  printf("IN%d\n",s[i+1]-48);
                  sum += (s[i+1]-48)*weight[loc];
                  //sum += int(s[i+1])*weight[loc];
               }
            }
         }
      }
      else //最后一位是字母
      {
         for(int i = 0; i < n-1 ; i++) //少循环一位
         {
            if (s[i] >= 65 && s[i]<= 90)
            {
               loc = get_loc(s[i]);
               if (s[i + 1] >= 65 && s[i + 1]<= 90) //如果下一位是字母
               {

                  sum += weight[loc];

                  printf("1%f\n", sum);
               }
               else  //如果下一位是数字
               {
                  sum += (s[i+1]-48)*weight[loc];
                  printf("2%f\n", sum);
               }
            }
         }
         loc = get_loc(s[n-1]);
         sum += weight[loc];
         printf("3%f\n", sum);
      }
   }
   printf("SUM %f",sum);
   system ("pause");
}