数据结构(一)二叉树 & avl树 & 红黑树 & B-树 & B+树 & B*树 & R树
参考文档:
avl树:http://lib.csdn.net/article/datastructure/9204
avl树:http://blog.csdn.net/javazejian/article/details/53892797
trie树:https://www.cnblogs.com/huangxincheng/archive/2012/11/25/2788268.html
b,b+,b* 树 :https://www.cnblogs.com/wjoyxt/p/5501706.html
b,b+ 树 & linux磁盘存储 :https://www.cnblogs.com/vincently/p/4526560.html
b,b+树 & mysql索引 & 索引的结构优化:http://blog.codinglabs.org/articles/theory-of-mysql-index.html
树:
树(Tree)是n(n≥0)个结点的有限集T,并且当n>0时满足下列条件:
(1)有且仅有一个特定的称为根(Root)的结点;
(2)当n>1时,其余结点可以划分为m(m>0)个互不相交的有限集T1、T2 、…、Tm,每个集Ti(1≤i≤m)均为树,且称为树T的子树(SubTree)。
特别地,不含任何结点(即n=0)的树,称为空树。
如下就是一棵树的结构:
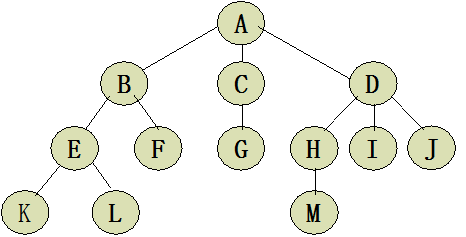
两种树:
- 有序树:若将树中每个结点的各子树看成是从左到右有次序的(即不能互换),则称该树为有序树
- 无序树:若将树中每个结点的各子树看成是从左到右无次序的(即可以互换),则称该树为无序树
多叉树的广度优先遍历与深度优先遍历
举个栗子:
多叉树 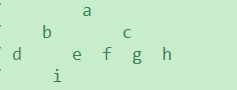
广度优先遍历:a b c d e f g h i
深度优先遍历:a b d e i c f g h (相当于二叉树的先序遍历)
实现:
public class MultiwayTree {
private static MultiwayNode root;
public MultiwayTree(){
// a
// b c
// d e f g h
// i
MultiwayNode h=new MultiwayNode("h");
MultiwayNode i=new MultiwayNode("i");
MultiwayNode g=new MultiwayNode("g");
MultiwayNode f=new MultiwayNode("f");
MultiwayNode d = new MultiwayNode("d");
MultiwayNode e = new MultiwayNode("e",i);
MultiwayNode b = new MultiwayNode("b", d, e);
MultiwayNode c = new MultiwayNode("c", f, g,h);
root = new MultiwayNode("a", b, c);
}
//深度优先遍历
static void depthFirstSearch(MultiwayNode node){
if(node==null){
return;
}
List<MultiwayNode> children=node.children;
if(children==null){
return;
}
System.out.print(node.value+" ");
for(MultiwayNode no:children){
depthFirstSearch(no);
}
}
//广度优先遍历
static void breadthFirstSearch(){
List<MultiwayNode> list=new ArrayList<MultiwayNode>();
list.add(root);
breadthFirstSearch(list);
}
//广度优先遍历
static void breadthFirstSearch(List<MultiwayNode> nodes){
List<MultiwayNode> level=new ArrayList<MultiwayNode>();
for(MultiwayNode node:nodes){
System.out.print(node.value+" ");
List<MultiwayNode> children=node.children;
level.addAll(children);
children.clear();
}
if(level.size()>0){
breadthFirstSearch(level);
}
}
public static void main(String[] args) {
MultiwayTree head=new MultiwayTree();
depthFirstSearch(head.root);
}
}
class MultiwayNode{
public String value;
public List<MultiwayNode> children=null;
public MultiwayNode(String value,MultiwayNode... nodes){
this.value=value;
children=new ArrayList<MultiwayNode>();
for(MultiwayNode node:nodes){
children.add(node);
}
}
}
二叉树:
二叉树是每个结点最多有两个孩子,且其子树有左右之分的有序树
二叉树的两个特殊形态
- 满二叉树:
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树
- 完全二叉树(Complete Binary Tree):
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树
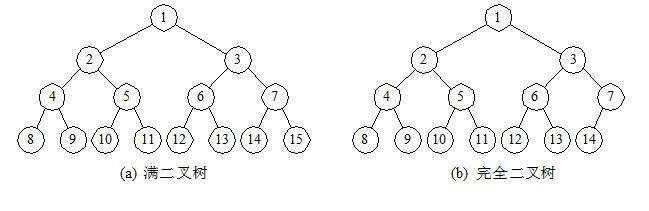
二叉树得到一般算法
求二叉树的最大深度:
int getMaxDeath(Node node) {
if (node == null) {
return 0;
}
int left = getMaxDeath(node.leftchild);
int right = getMaxDeath(node.leftchild);
return Math.max(left, right) + 1;
}
求二叉树的最小深度:
int getMinDepth(Node root) {
if (root == null) {
return 0;
}
int left=getMinDepth(root.leftchild);
int right=getMinDepth(root.rightchild);
return Math.min(left, right) + 1;
}
求二叉树的总节点数
//求二叉树的节点总数
int getTotalNumNode(Node root) {
if (root == null) {
return 0;
}
int left = getTotalNumNode(root.leftchild);
int right = getTotalNumNode(root.rightchild);
return left + right + 1;
}
求二叉树种的叶子节点的个数
// 求二叉树中叶子节点的个数
int getNumForLeafNode(Node root) {
if (root == null) {
return 0;
}
if (root.leftchild == null && root.rightchild == null) {
return 1;
}
return getNumForLeafNode(root.leftchild) + getNumForLeafNode(root.rightchild);
}
求二叉树中第k层节点的个数
//求二叉树中第k层节点的个数
int getNumOfkLevelNode(Node root, int k) {
if (root == null || k < 1) {
return 0;
}
if (k == 1) {
return 1;
}
int numsLeft = getNumOfkLevelNode(root.leftchild, k - 1);
int numsRight = getNumOfkLevelNode(root.rightchild, k - 1);
return numsLeft + numsRight;
}
两个二叉树是否完全相同
boolean isSameTree(Node t1, Node t2) {
if (t1 == null && t2 == null) {
return true;
} else if (t1 == null || t2 == null) {
return false;
}
if(!t1.getValue().equals(t2.getValue())){
return false;
}
boolean left = isSameTree(t1.leftchild, t2.leftchild);
boolean right = isSameTree(t1.rightchild, t2.rightchild);
return left && right;
}
两个二叉树是否互为镜像
//两个二叉树是否互为镜像
boolean isMirror(Node t1, Node t2) {
if (t1 == null && t2 == null) {
return true;
}
if (t1 == null || t2 == null) {
return false;
}
if (!t1.getValue().equals(t2.getValue())) {
return false;
}
return isMirror(t1.leftchild, t2.rightchild) && isMirror(t1.rightchild, t2.leftchild);
}
翻转/镜像二叉树
// 翻转二叉树or镜像二叉树
Node mirrorTreeNode(Node root) {
if (root == null) {
return null;
}
Node left = mirrorTreeNode(root.leftchild);
Node right = mirrorTreeNode(root.rightchild);
root.leftchild = right;
root.rightchild = left;
return root;
}
前根序遍历 父节点->左孩子->右孩子
// 前根序遍历 父节点->左孩子->右孩子
public void preOrder(Node no) {
if (no != null) {
printValue(no);
preOrder(no.getLeftchild());
preOrder(no.getRightchild());
}
}
中根序遍历 左孩子->父节点->右孩子
//中根序遍历 左孩子->父节点->右孩子
public void inOrder(Node no) {
if (no != null) {
inOrder(no.getLeftchild());
printValue(no);
inOrder(no.getRightchild());
}
}
后根序遍历 左孩子->右孩子->父节点
// 后根序遍历 左孩子->右孩子->父节点
public void reOrder(Node no) {
if (no == null) {
return;
}
reOrder(no.getLeftchild());
reOrder(no.getRightchild());
printValue(no);
}
二叉查找树(Binary Sort Tree)(排序树/搜索树)
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
1) 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2) 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
3) 左、右子树也分别为二叉排序树;
4) 没有键值相等的节点。

二叉查找树的性质:
对二叉查找树进行中序遍历,即可得到有序的数列
二叉查找树的时间复杂度:
它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡。我们追求的是在最坏的情况下仍然有较好的时间复杂度,这就是平衡查找树设计的初衷
平衡二叉查找树(Balanced Binary Tree)(简称平衡二叉树)(avl树):
它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
平衡因子(bf):
结点的左子树的深度减去右子树的深度,那么显然-1<=bf<=1
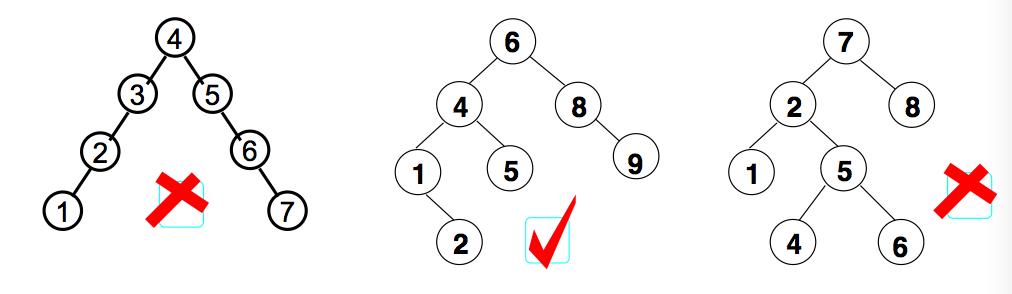
查询 & 插入 & 删除 时间复杂度:O(logn)
应用:
- windows对进程地址空间的管理用到了AVL树
// 判断是否为平衡二叉树
public boolean isBalanced(Node root, int depth) {
if (root == null) {
depth = 0;
return true;
}
int leftDepth = 0;
int rigthDepth = 0; boolean isLeftBalanced = isBalanced(root.getLeftchild(), leftDepth);
boolean isRightBalanced = isBalanced(root.getLeftchild(), rigthDepth); if (isLeftBalanced && isRightBalanced) {
int diff = leftDepth - rigthDepth; if (diff <= 1 || diff >= -1) {
depth = leftDepth > rigthDepth ? leftDepth : rigthDepth + 1;
return true;
}
}
return false;
}
- 节点是红色或黑色
- 根是黑色
- 所有叶子都是黑色(叶子是NIL节点)
- 从每个叶子到根的所有路径上不能有两个连续的红色节点
- 从任一节点到其每个叶子的所有简单路径 都包含相同数目的黑色节点
查询 & 插入 & 删除 时间复杂度:O(logn)
应用:
- 广泛用在C++的STL中。如map和set都是用红黑树实现的
- 著名的linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块
- epoll在内核中的实现,用红黑树管理事件块
- nginx中,用红黑树管理timer等
- Java的TreeMap实现
红黑树 vs avl树
- 插入:如果插入一个node引起了树的不平衡,AVL和RB-Tree都是最多只需要2次旋转操作,即两者都是O(1);
- 删除:最坏情况下,AVL需要维护从被删node到root这条路径上所有node的平衡性,因此需要旋转的量级O(logN),而RB-Tree最多只需3次旋转,只需要O(1)的复杂度。AVL的结构相较RB-Tree来说更为平衡,在插入和删除node更容易引起Tree的unbalance,因此在大量数据需要插入或者删除时,AVL需要rebalance的频率会更高。因此,RB-Tree在需要大量插入和删除node的场景下,效率更高。
- 查找:由于AVL高度平衡,因此AVL的search效率更高
map的实现只是折衷了两者在search、insert以及delete下的效率。总体来说,RB-tree的统计性能是高于AVL的。
Trie树(字典树)
B-树(平衡多路查找树)
一棵m阶的b树满足下列条件:
- 每个结点至多拥有m棵子树根结点至少拥有两颗子树(存在子树的情况下)
- 除了根结点以外,其余每个分支结点至少拥有 m/2 棵子树
- 所有的叶结点都在同一层上
- 有 k 棵子树的分支结点则存在 k-1 个关键码,关键码按照递增次序进行排列
- 关键字数量需要满足ceil(m/2)-1 <= n <= m-1
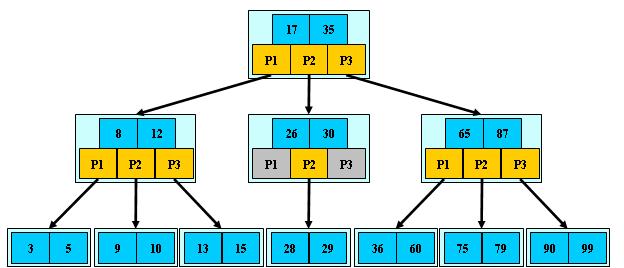
b树的特性:
- 关键字集合分布在整颗树中
- 任何一个关键字出现且只出现在一个结点中
- 搜索有可能在非叶子结点结束
- 其搜索性能等价于在关键字全集内做一次二分查找
查询,插入,删除 时间复杂度:O(logn)
B+树
B+树是B-树的变体,也是一种多路搜索树:
其定义基本与B-树同,除了:
- 非叶子结点的子树指针与关键字个数相同
- 非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间)
- 为所有叶子结点增加一个链指针
- 所有关键字都在叶子结点出现
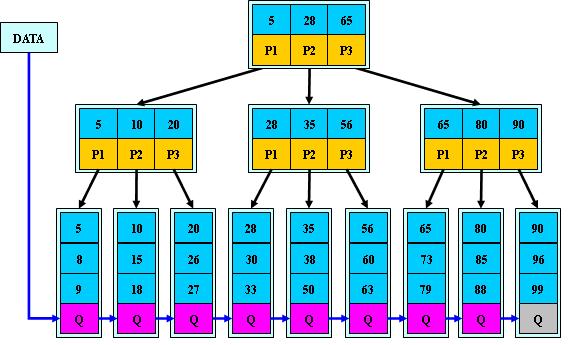 B+的特性:
B+的特性:
- 所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的
- 不可能在非叶子结点命中
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层
- 更适合文件索引系统
查询,插入,删除 时间复杂度:O(logn)
应用:InnoDB索引 MyISAM索引
B*树
是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针
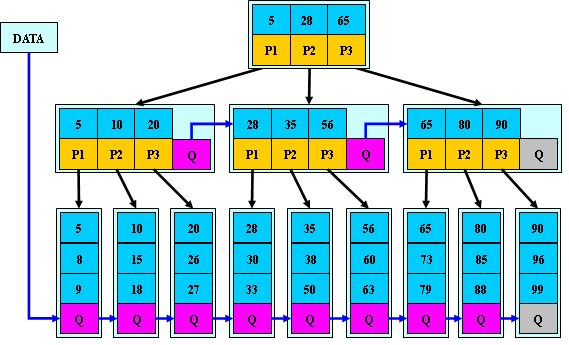
B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3
(代替B+树的1/2);
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据
复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父
结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分
数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字
(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之
间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;
所以,B*树分配新结点的概率比B+树要低,空间使用率更高;
R树
R树是B树在高维空间的扩展,是一棵平衡树。每个R树的叶子结点包含了多个指向不同数据的指针,这些数据可以是存放在硬盘中的,也可以是存在内存中。根据R树的这种数据结构,当我们需要进行一个高维空间查询时,我们只需要遍历少数几个叶子结点所包含的指针,查看这些指针指向的数据是否满足要求即可。这种方式使我们不必遍历所有数据即可获得答案,效率显著提高。下图1是R树的一个简单实例:
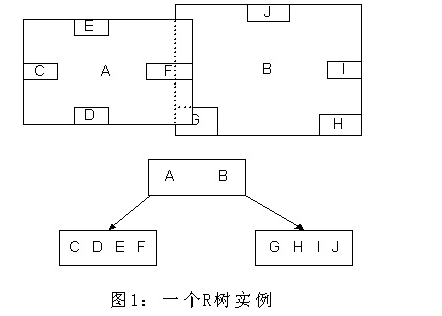
数据结构(一)二叉树 & avl树 & 红黑树 & B-树 & B+树 & B*树 & R树的更多相关文章
- 树:BST、AVL、红黑树、B树、B+树
我们这个专题介绍的动态查找树主要有: 二叉查找树(BST),平衡二叉查找树(AVL),红黑树(RBT),B~/B+树(B-tree).这四种树都具备下面几个优势: (1) 都是动态结构.在删除,插入操 ...
- 数据结构与算法--从平衡二叉树(AVL)到红黑树
数据结构与算法--从平衡二叉树(AVL)到红黑树 上节学习了二叉查找树.算法的性能取决于树的形状,而树的形状取决于插入键的顺序.在最好的情况下,n个结点的树是完全平衡的,如下图"最好情况&q ...
- AVL树,红黑树
AVL树 https://baike.baidu.com/item/AVL%E6%A0%91/10986648 在计算机科学中,AVL树是最先发明的自平衡二叉查找树.在AVL树中任何节点的两个子树的高 ...
- 浅谈AVL树,红黑树,B树,B+树原理及应用(转)
出自:https://blog.csdn.net/whoamiyang/article/details/51926985 背景:这几天在看<高性能Mysql>,在看到创建高性能的索引,书上 ...
- 浅谈AVL树,红黑树,B树,B+树原理及应用
背景:这几天在看<高性能Mysql>,在看到创建高性能的索引,书上说mysql的存储引擎InnoDB采用的索引类型是B+Tree,那么,大家有没有产生这样一个疑问,对于数据索引,为什么要使 ...
- JAVA中的数据结构 - 真正的去理解红黑树
一, 红黑树所处数据结构的位置: 在JDK源码中, 有treeMap和JDK8的HashMap都用到了红黑树去存储 红黑树可以看成B树的一种: 从二叉树看,红黑树是一颗相对平衡的二叉树 二叉树--&g ...
- 大名鼎鼎的红黑树,你get了么?2-3树 绝对平衡 右旋转 左旋转 颜色反转
前言 11.1新的一月加油!这个购物狂欢的季节,一看,已囊中羞涩!赶紧来恶补一下红黑树和2-3树吧!红黑树真的算是大名鼎鼎了吧?即使你不了解它,但一定听过吧?下面跟随我来揭开神秘的面纱吧! 一.2-3 ...
- B树 B+树 红黑树
B-Tree(B树) 具体讲解之前,有一点,再次强调下:B-树,即为B树.因为B树的原英文名称为B-tree,而国内很多人喜欢把B-tree译作B-树,其实,这是个非常不好的直译,很容易让人产生误解. ...
- 数据结构图解(递归,二分,AVL,红黑树,伸展树,哈希表,字典树,B树,B+树)
递归反转 二分查找 AVL树 AVL简单的理解,如图所示,底部节点为1,不断往上到根节点,数字不断累加. 观察每个节点数字,随意选个节点A,会发现A节点的左子树节点或右子树节点末尾,数到A节点距离之差 ...
随机推荐
- git 从远程克隆代码并实现分支开发,合并分支,上传本地代码到远程
首先确认你已经安装了git 1.克隆远程代码到本地的操作 git clone 地址 打开git操作命令行 鼠标右键点击 复制需要克隆的项目的地址类似下面的ssh 输入命令进行 ...
- Java 之 List 接口
一.List 接口介绍 java.util.List 接口继承自 Collection 接口,是单列集合的一个重要分支,习惯性地会将实现了 List 接口的对象称为 List 集合. 在 List 集 ...
- 英语bitellos钻石bitellos单词
大颗粒的钻石叫做bitellos,四大钻石指的就是“摄政王”.“南非之星”.“蓝色希望”和“光明之山”四颗钻石.经过琢磨的钻石光彩夺目.灿烂无比,历来被誉为“宝石之王”,科研领域里大颗粒的钻石叫做bi ...
- 面试题:android的安全机制有哪些
1 uid . gid . gids Android 的权限分离的基础是建立在 Linux 已有的 uid . gid . gids 基础上的 . UID: Android 在 安装一个应用程序,就会 ...
- xen虚拟化环境安装
1. 操作系统安装 OEL下载地址大全: http://koumm.blog.51cto.com/703525/1283801 # uname -a Linux localhost 2.6.39-40 ...
- Python 数学运算的函数
不需要导入模块(内置函数) 函数 返回值 ( 描述 ) abs(x) 返回绝对值 max(x1, x2,...) 最大值,参数可以为序列. min(x1, x2,...) 最小值,参数可以为序列. p ...
- 浅谈布隆过滤器Bloom Filter
先从一道面试题开始: 给A,B两个文件,各存放50亿条URL,每条URL占用64字节,内存限制是4G,让你找出A,B文件共同的URL. 这个问题的本质在于判断一个元素是否在一个集合中.哈希表以O(1) ...
- 生产环境碰到系统CPU飙高和频繁GC系统反应慢,你要怎么排查?(转)
处理过线上问题的同学基本上都会遇到系统突然运行缓慢,CPU 100%,以及Full GC次数过多的问题.当然,这些问题的最终导致的直观现象就是系统运行缓慢,并且有大量的报警.本文主要针对系统运行缓慢这 ...
- centos 启动 oracle
source .bash_profile su - oracle //切换到自己的oracle账户 lsnrctl start //启动oracle监听 sqlplus /nolog //登录 ...
- Codeforces C Match Points(二分贪心)
题目描述: Match Points time limit per test 2 seconds memory limit per test 256 mega bytes input standard ...
