HDOJ-1100 Trees made to order

一、题目链接

http://acm.hdu.edu.cn/showproblem.php?pid=1100

二、题目分析

对二叉树的所有形态顺序编号，编号规则是：节点数越多的编号越大；节点数相等，左子树节点数越多的越大；节点数相等，左子树节点数也相等，则依此规则比较右子树。

现给定一个正整数，依题目要求输出对应编号的二叉树形态。

三、求解思路

由题目输出格式要求，很直观地联想到使用深度优先搜索dfs，以当前二叉树对应的编号为条件，依次递归输出左子树和右子树。

 1 int main(void) {
 2     int n;
 3     unsigned int arr[20] = {0};
 4
 5     init(arr, 20);
 6
 7     while (scanf("%d", &n) != EOF && n != 0) {
 8         dfs(n, arr, 20);
 9         printf("\n");
10     }
11
12     return 0;
13 }

其中arr存储的是不同节点数对应的二叉树形态数，即arr[i]表示有i个节点的二叉树总共有多少种形态。

 1 void dfs(int n, unsigned int *arr, int num) {
 2
 3     int left, right;
 4
 5     if (n == 1) {
 6         printf("X");
 7         return ;
 8     }
 9
10     getChildren(&left, &right, n, arr, num);
11
12     if (left != 0) {
13         printf("(");
14         dfs(left, arr, num);
15         printf(")");
16     }
17     printf("X");
18     if (right != 0) {
19         printf("(");
20         dfs(right, arr, num);
21         printf(")");
22     }
23 }

通过getChildren得到左右子树对应的编号，然后递归搜索即可。

计算左右子树对应序号的思路：

1. 计算总节点数nall、左子树节点数nleft和右子树节点数nright；

2. 在计算总节点数和左子树节点数的同时，刨除所有总节点数小于nall的二叉树形态，刨除所有左子树节点数小于nleft的二叉树形态；

3. 那么下面如何确定当前左子树是nleft个节点的二叉树中的第几个？当前右子树又是nright个节点的二叉树中的第几个？且看一例

   

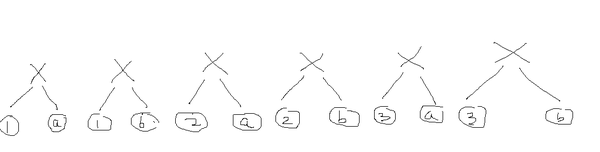
4. 这里假定左子树有三种形态，分别是1,2,3，右子树有两种形态，分别是a,b。额，其实有哪个节点总数对应三种二叉树形态，这里只是举例子

5. 由这个小例子可以看出，要想确定左右子树对应的序号，需要依据右子树的形态数 ，对应的就是代码中的div，rem以及下面计算的blablabla

 1 void getChildren(int *left, int *right, int n, unsigned int *arr, int num) {
 2
 3     int i;
 4     int nall, nleft, nright;
 5     int div, rem;
 6
 7     for (i = 1; i < num; i++) {
 8         if ((unsigned)n > arr[i]) {
 9             n -= arr[i];
10         } else {
11             nall = i;
12             break;
13         }
14     }
15
16     for (i = 0; i < nall; i++) {
17         if ((unsigned)n > arr[i] * arr[nall - i - 1]) {
18             n -= arr[i] * arr[nall - i - 1];
19         } else {
20             nleft = i;
21             break;
22         }
23     }
24     nright = nall - nleft - 1;
25
26     div = n / arr[nright];
27     rem = n % arr[nright];
28
29     *left = *right = 0;
30
31     if (nleft != 0) {
32         for (i = 1; i < nleft; i++) {
33             *left += arr[i];
34         }
35         *left += rem == 0 ? div : div + 1;
36
37     if (nright != 0) {
38         for (i = 1; i < nright; i++) {
39             *right += arr[i];
40         }
41         *right += rem == 0 ? arr[nright] : rem;
42     }
43 }

嗯，差不多就这些了。为什么是arr[20]？怎么计算i个节点对应的二叉树形态数？wiki一下Catalan numbers吧。

附完整代码：

  1 /* http://acm.hdu.edu.cn/showproblem.php?pid=1100 */
  2
  3 #include <stdio.h>
  4
  5 void    init(unsigned int *arr, int N);
  6 void    dfs(int n, unsigned int *arr, int num);
  7 void    getChildren(int *left, int *right, int n, unsigned int *arr, int num);
  8
  9 int main(void)
 10 {
 11     int n;
 12     unsigned int arr[20] = {0};
 13
 14     init(arr, 20);
 15
 16     while (scanf("%d", &n) != EOF && n != 0) {
 17         dfs(n, arr, 20);
 18         printf("\n");
 19     }
 20
 21     return 0;
 22 }
 23
 24 void init(unsigned int *arr, int N)
 25 {
 26     int i, j;
 27
 28     arr[0] = arr[1] = 1;
 29     for (i = 2; i < N; i++) {
 30         for (j = 0; j < i; j++) {
 31             arr[i] += arr[j] * arr[i - j - 1];
 32         }
 33     }
 34 }
 35
 36 void dfs(int n, unsigned int *arr, int num)
 37 {
 38     int left, right;
 39
 40     if (n == 1) {
 41         printf("X");
 42         return ;
 43     }
 44
 45     getChildren(&left, &right, n, arr, num);
 46
 47     if (left != 0) {
 48         printf("(");
 49         dfs(left, arr, num);
 50         printf(")");
 51     }
 52     printf("X");
 53     if (right != 0) {
 54         printf("(");
 55         dfs(right, arr, num);
 56         printf(")");
 57     }
 58 }
 59
 60 void getChildren(int *left, int *right, int n, unsigned int *arr, int num)
 61 {
 62     int i;
 63     int nall, nleft, nright;
 64     int div, rem;
 65
 66     for (i = 1; i < num; i++) {
 67         if ((unsigned)n > arr[i]) {
 68             n -= arr[i];
 69         } else {
 70             nall = i;
 71             break;
 72         }
 73     }
 74
 75     for (i = 0; i < nall; i++) {
 76         if ((unsigned)n > arr[i] * arr[nall - i - 1]) {
 77             n -= arr[i] * arr[nall - i - 1];
 78         } else {
 79             nleft = i;
 80             break;
 81         }
 82     }
 83     nright = nall - nleft - 1;
 84
 85     div = n / arr[nright];
 86     rem = n % arr[nright];
 87
 88     *left = *right = 0;
 89
 90     if (nleft != 0) {
 91         for (i = 1; i < nleft; i++) {
 92             *left += arr[i];
 93         }
 94         *left += rem == 0 ? div : div + 1;
 95
 96     if (nright != 0) {
 97         for (i = 1; i < nright; i++) {
 98             *right += arr[i];
 99         }
100         *right += rem == 0 ? arr[nright] : rem;
101     }
102 }