【CSP模拟赛】益智游戏（最短路（DJSPFA）&拓扑排序）

题目描述

小P和小R在玩一款益智游戏。游戏在一个正权有向图上进行。 小P 控制的角色要从A 点走最短路到B 点，小R 控制的角色要从C 点走最短路到D 点。 一个玩家每回合可以有两种选择，移动到一个相邻节点或者休息一回合。 假如在某一时刻，小P 和小R 在相同的节点上，那么可以得到一次特殊奖励，但是在每 个节点上最多只能得到一次。 求最多能获得多少次特殊奖励

输入格式

第一行两个整数n，m 表示有向图的点数和边数。 接下来m 行每行三个整数xi，yi，li，表示从xi 到yi 有一条长度为li 的边。 最后一行四个整数A，B，C，D，描述小P 的起终点，小R 的起终点。

输出格式

输出一个整数表示最多能获得多少次特殊奖励。若小P不能到达B点或者小R不能到达D点则输出-1。

输入样例

5 5
  1 2 1
  2 3 2
  3 4 4
  5 2 3
  5 3 5
  1 3 5 4

输出样例

2
提示
  对于30%的数据，满足n≤50 对于60%的数据，满足n≤1000，m≤5000 对于100%的数据，满足n≤50000，m≤200000，1≤li≤500000000

分析

A到B，C到D的最短路有很多条。

但对于任意一条A到B的最短路和任意一条C到D的最短路如果他们有交点，那交点一定是连续的，否则一定存在交点更多的两条最短路。

如图

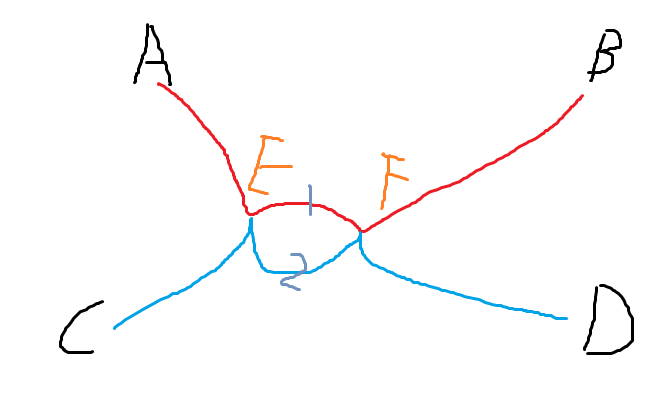
如果A到B的路径（红色）与C到D的路径（蓝色）有不连续的交点E与F

那么E通过路径1到达F与E通过路径2到达F的距离应该是一样，否则路径A-B，路径C-D中有一条不是最短路

此时，若A走到达E后走路径2到达F会与路径C-D有更多交点

即走绿色这条路<-也是最短路

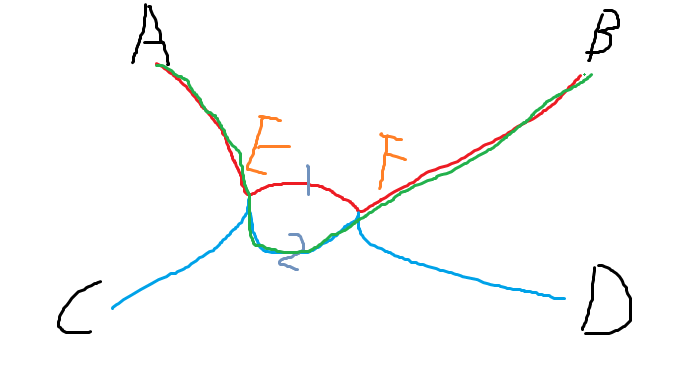
所以最优方案中特殊奖励的点一定是连续的。

于是我们可以用同时在A-B最短路上和C-D最短路上的有向边构成一个新图

那么新图一定是一个有向无环图，但不一定联通

最后对新图拓扑排序dp最长链即可

代码（给你们演示一下堆优化的SPFA）

#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=;
const int maxm=;
struct node{int id;long long d;};
bool operator <(node a,node b){return a.d>b.d;}
int info[maxn],nx[maxm<<],v[maxm<<],w[maxm<<],re[maxm<<];long long d[][maxn];
int n,m,en,ans,ecnt,p[],dp[maxn],vis[maxn],inp[maxn],top[maxn],lef[maxm<<];priority_queue<node>q;
void add(int u1,int v1,int w1,int r){nx[++ecnt]=info[u1];info[u1]=ecnt;v[ecnt]=v1;w[ecnt]=w1;re[ecnt]=r;}
void SPFA(int k)
{
    memset(vis,,sizeof vis);
    d[k][p[k]]=;q.push((node){p[k],});
    while(!q.empty())
    {
        node nw=q.top();q.pop();
        if(vis[nw.id]==)continue;vis[nw.id]=;d[k][nw.id]=nw.d;
        for(int i=info[nw.id];i;i=nx[i])
        if(!((k%)^re[i])&&d[k][v[i]]>nw.d+w[i])q.push((node){v[i],nw.d+w[i]});
    }
}
int main()
{
    scanf("%d%d",&n,&m);memset(d,0x7f,sizeof d);
    for(int i=,u1,v1,w1;i<=m;i++)scanf("%d%d%d",&u1,&v1,&w1),add(u1,v1,w1,),add(v1,u1,w1,);
    for(int k=;k<=;k++)scanf("%d",&p[k]),SPFA(k);
    if(d[][p[]]==d[][]||d[][p[]]==d[][]){puts("-1");return ;}
    for(int x=;x<=n;x++)
    {
        for(int e=info[x];e;e=nx[e])
        if(re[e]&&d[][x]+w[e]+d[][v[e]]==d[][p[]]&&d[][x]+w[e]+d[][v[e]]==d[][p[]])
        lef[e]=,inp[v[e]]++;
    }
    for(int x=;x<=n;x++)if(inp[x]==)top[++en]=x,dp[x]=;
    for(int i=;i<=en;i++)
    {
        int nw=top[i];
        for(int e=info[nw];e;e=nx[e])
            if(lef[e])
            {
                dp[v[e]]=max(dp[v[e]],dp[nw]+);
                ans=max(ans,dp[v[e]]);inp[v[e]]--;
                if(!inp[v[e]])top[++en]=v[e];
            }
    }
    printf("%d\n",ans);
}