ML- 线性回归推导

线性回归, 这部分算是我最为擅长的了, 真的不吹, 6年经验, 我高中时代就已经会推导了, 当然是最最小二乘法和统计学(假设检验, 参数分布等)的角度.

后来上了大学, 又是从最小二乘和统计学角度, 最终呢, 还是从线性代数(向量投影) 和 微积分 角度 + 代码实现给整了一遍, 再后来就是ML, 撸了一遍梯度下降, 嗯, 整体感悟就是,对一个事物的认知, 需要一个时间的过程和实践.

正如古人所讲, 纸上来得终觉浅, 绝知此事要躬行.

回归模型

数据:

\((y_i, X_{i1}, X_{i2}...X_{ip}), \ i = 1,2,3...n\)

y 是一个向量, X是一个矩阵

样本 X 是一个 nxp 的矩阵, 每一行是表示一个样本, 对应一个目标值

y 是由这 p 个(维) 列向量 线性组合 而成, 因此叫线性回归.

模型:

\(y_i = \beta_0 +\beta_1 X_{i1} + \beta_2 X_{i2} + \beta_p X_{il} + \epsilon_i, \ i=1,2,...n\)

\(\epsilon \backsim N(0, \sigma)\) , 为啥误差的均值是0, 参考大数定律呗.(总体和样本的关系)

写为矩阵的形式:

\(y = X\beta + \epsilon\)

X 是 nxp, \(\beta\) 是 px1, y 是 nx1

误差函数:

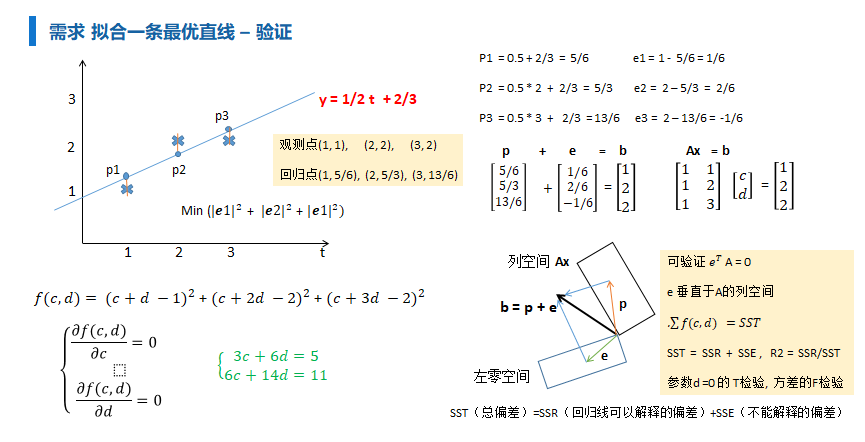
\(J(\beta) = ||X\beta - y||^2\)

\(X\beta - y\) 表示两个列向量相减, 表示两个向量 相似, 如果相似, 则对应的分量应该接近0, 这样得到的差向量, 对其求模, 就可衡量了.

当然, 之前在SVM 衡量相似 用的是 内积, 方法很多啦, 可解释就好.

最线性代数(投影)求解 \(\beta\)

涉及的现代知识有些多,不过这是必须的, 当你认识到本质的时候, 你会发现, 原来世界如此美妙.

这是为方便说明投影概念,我在2017年画的几张图.

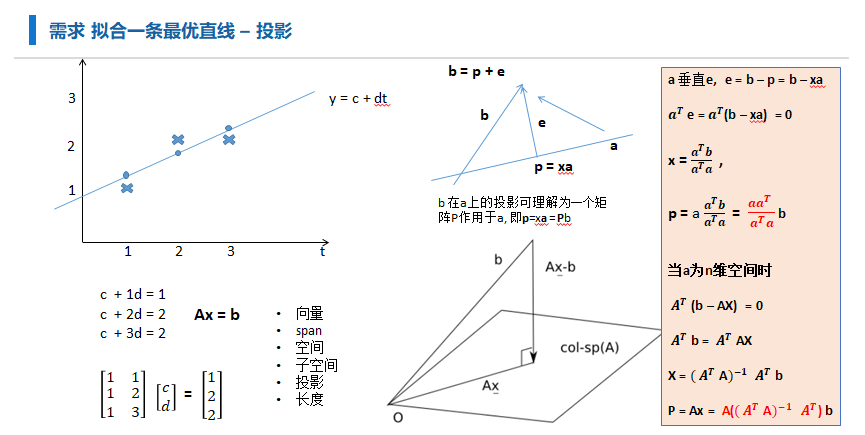
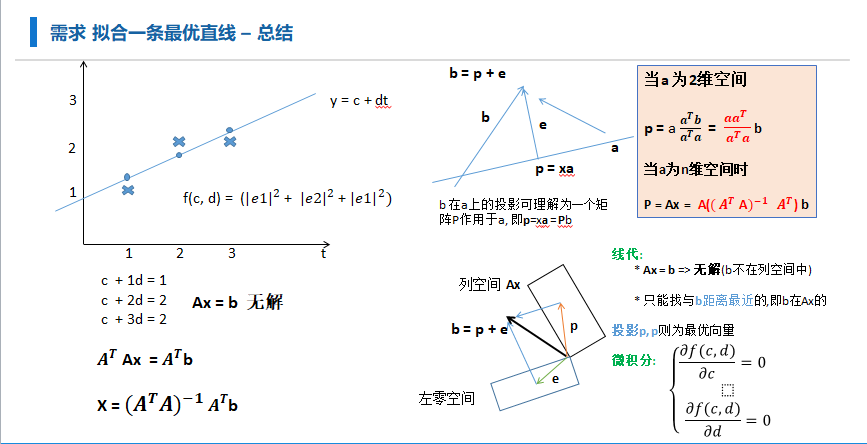
\(\beta = (X^TX)^{-1}X^Ty\)

从向量投影角度: 参考MIT <线性代数> 最小二乘

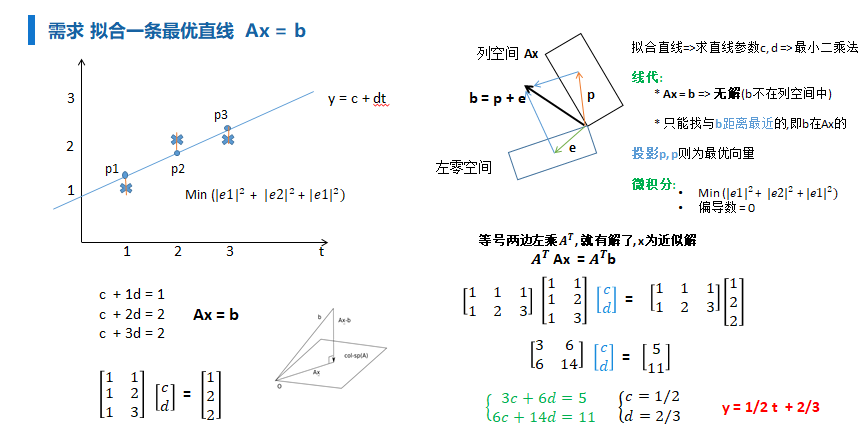
\(y = X\beta\) 无解, 做一个变换, 等号两边左乘 \(X^T\) 求近似解(空间投影找近似)

\(X^Ty = X^TX\beta\)

$即: \beta = (X^TX){-1}X^Ty $

感觉这是一个历史问题, 最小二乘在17-18世纪是非常火的, 但也是受到很多怀疑, 于是高斯这批人,就从概率的角度, 再对最小二乘法进行了一个推广, 也就差不多时大二的概率论书中的那个样子, 用似然来整的.

从微分(梯度)角度求解 \(\beta\)

\(J(\beta) = ||X\beta -y||^2\)

$ = (X\beta -y)^T (X\beta -y)$

\(= (\beta^T X^T -y^T) (X\beta -y)\)

\(=\beta^T X^T X \beta - \beta^T X^Ty - y^TX \beta + y^Ty\)

然后对 beta 求 偏导 = 0 即可

矩阵求导: http://www2.imm.dtu.dk/pubdb/views/publication_details.php?id=3274

矩阵求导讲起来有点复杂, 我目前都是记住了一些常用的形式的, 哈哈, CV 调参侠 一枚

\(\nabla_\beta J(\beta) = 0 = 2X^TX \beta - X^Ty - X^Ty\)

\(即X^TX\beta = X^Ty\)

$即: \beta = (X^TX){-1}X^Ty $

矩阵来写确实很优美简洁, 但有些抽象,尤其是求导, 这样还有啥好处呢? 当然是非常容易写代码了呀

人们来理解矩阵是非常困难的 - 涉及很多思想和求解

but

计算机理解矩阵是非常容易的 - 就是多维数组而已啦

只需一行代码求解 参数 beta

def 求解线性回归_beta(A, b):
    """return 值 = (