PAT_A1018#Public Bike Management

Source:

PAT A1018 Public Bike Management (30 分)

Description:

There is a public bike service in Hangzhou City which provides great convenience to the tourists from all over the world. One may rent a bike at any station and return it to any other stations in the city.

The Public Bike Management Center (PBMC) keeps monitoring the real-time capacity of all the stations. A station is said to be in perfect condition if it is exactly half-full. If a station is full or empty, PBMC will collect or send bikes to adjust the condition of that station to perfect. And more, all the stations on the way will be adjusted as well.

When a problem station is reported, PBMC will always choose the shortest path to reach that station. If there are more than one shortest path, the one that requires the least number of bikes sent from PBMC will be chosen.

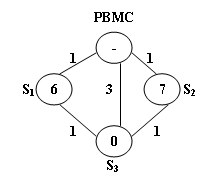
The above figure illustrates an example. The stations are represented by vertices and the roads correspond to the edges. The number on an edge is the time taken to reach one end station from another. The number written inside a vertex S is the current number of bikes stored at S. Given that the maximum capacity of each station is 10. To solve the problem at S​3​​, we have 2 different shortest paths:

• PBMC -> S​1​​ -> S​3​​. In this case, 4 bikes must be sent from PBMC, because we can collect 1 bike from S​1​​ and then take 5 bikes to S​3​​, so that both stations will be in perfect conditions.

• PBMC -> S​2​​ -> S​3​​. This path requires the same time as path 1, but only 3 bikes sent from PBMC and hence is the one that will be chosen.

Input Specification:

Each input file contains one test case. For each case, the first line contains 4 numbers: C​max​​ (≤), always an even number, is the maximum capacity of each station; N (≤), the total number of stations; S​p​​, the index of the problem station (the stations are numbered from 1 to N, and PBMC is represented by the vertex 0); and M, the number of roads. The second line contains N non-negative numbers C​i​​ (,) where each C​i​​ is the current number of bikes at S​i​​ respectively. Then Mlines follow, each contains 3 numbers: S​i​​, S​j​​, and T​ij​​ which describe the time T​ij​​ taken to move betwen stations S​i​​ and S​j​​. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print your results in one line. First output the number of bikes that PBMC must send. Then after one space, output the path in the format: 0. Finally after another space, output the number of bikes that we must take back to PBMC after the condition of S​p​​is adjusted to perfect.

Note that if such a path is not unique, output the one that requires minimum number of bikes that we must take back to PBMC. The judge's data guarantee that such a path is unique.

Sample Input:

10 3 3 5
6 7 0
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1

Sample Output:

3 0->2->3 0

Keys:

• 最短路径

Code:

 /*
 Data: 2019-04-20 19:10:26
 Problem: PAT_A1018#Public Bike Management
 AC: 34:36

 题目大意：
 站点最佳状态时，有一半的自行车；
 从起点选择最短路径终点，路径上的其他站点同样调整至最佳状态（补充/回收）；
 多条最短路径时，选择需要携带且回收数量最少的最条路径
 输入：
 第一行给出，最大容量Cmax，结点数N，Sp终点（默认起点为0），路径数M
 第二行给出，各站点现有库存Ci
 输出；
 携带车辆数，路径，回收车辆数
 */

 #include<cstdio>
 #include<vector>
 #include<algorithm>
 using namespace std;
 const int M=,INF=1e9;
 int grap[M][M],vis[M],d[M],c[M];
 int n,m,Cmax,st=,dt,optSent=INF,optBring=INF;
 vector<int> temp,opt,pre[M];

 void Dijskra(int s)
 {
     fill(vis,vis+M,);
     fill(d,d+M,INF);
     d[s]=;
     for(int i=; i<=n; i++)
     {
         int u=-,Min=INF;
         for(int j=; j<=n; j++)
         {
             if(vis[j]== && d[j]<Min)
             {
                 u=j;
                 Min=d[j];
             }
         }
         if(u==-)   return;
         vis[u]=;
         for(int v=; v<=n; v++)
         {
             if(vis[v]== && grap[u][v]!=INF)
             {
                 if(d[u]+grap[u][v] < d[v])
                 {
                     d[v]=d[u]+grap[u][v];
                     pre[v].clear();
                     pre[v].push_back(u);
                 }
                 else if(d[u]+grap[u][v]==d[v])
                     pre[v].push_back(u);
             }
         }
     }
 }

 void DFS(int v)
 {
     if(v == st)
     {
         int sent=,bring=;
         for(int i=temp.size()-; i>=; i--)
         {
             int v = temp[i];
             if(bring+(c[v]-Cmax/) > )
                 bring = bring + (c[v]-Cmax/);
             else
             {
                 sent += (Cmax/-bring-c[v]);
                 bring=;
             }
         }
         if(sent < optSent)
         {
             optSent = sent;
             optBring = bring;
             opt = temp;
         }
         else if(sent==optSent && bring<optBring)
         {
             optBring = bring;
             opt = temp;
         }
         return;
     }

     temp.push_back(v);
     for(int i=; i<pre[v].size(); i++)
         DFS(pre[v][i]);
     temp.pop_back();
 }

 int main()
 {
 #ifdef ONLINE_JUDGE
 #else
     freopen("Test.txt", "r", stdin);
 #endif // ONLINE_JUDGE

     fill(grap[],grap[]+M*M,INF);
     scanf("%d%d%d%d", &Cmax,&n,&dt,&m);
     for(int i=; i<=n; i++)
         scanf("%d", &c[i]);
     for(int i=; i<m; i++)
     {
         int v1,v2;
         scanf("%d%d",&v1,&v2);
         scanf("%d", &grap[v1][v2]);
         grap[v2][v1]=grap[v1][v2];
     }
     Dijskra(st);
     DFS(dt);
     printf("%d %d", optSent,st);
     for(int i=opt.size()-; i>=; i--)
         printf("->%d", opt[i]);
     printf(" %d", optBring);

     return ;
 }