C. Searching for Graph(cf)

C. Searching for Graph

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's call an undirected graph of n vertices p-interesting, if the following conditions fulfill:

• the graph contains exactly 2n + p edges;
• the graph doesn't contain self-loops and multiple edges;
• for any integer k (1 ≤ k ≤ n), any subgraph consisting of k vertices contains at most 2k + p edges.

A subgraph of a graph is some set of the graph vertices and some set of the graph edges. At that, the set of edges must meet the condition: both ends of each edge from the set must belong to the chosen set of vertices.

Your task is to find a p-interesting graph consisting of n vertices.

Input

The first line contains a single integer t (1 ≤ t ≤ 5) — the number of tests in the input. Next t lines each contains two space-separated integers: n, p (5 ≤ n ≤ 24; p ≥ 0; 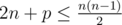) — the number of vertices in the graph and the interest value for the appropriate test.

It is guaranteed that the required graph exists.

Output

For each of the t tests print 2n + p lines containing the description of the edges of a p-interesting graph: the i-th line must contain two space-separated integers a_i, b_i (1 ≤ a_i, b_i ≤ n; a_i ≠ b_i) — two vertices, connected by an edge in the resulting graph. Consider the graph vertices numbered with integers from 1 to n.

Print the answers to the tests in the order the tests occur in the input. If there are multiple solutions, you can print any of them.

Sample test(s)

input

1
6 0

output

1 2
1 3
1 4
1 5
1 6
2 3
2 4
2 5
2 6
3 4
3 5
3 6

这个题是A题的水平额。。是在考题意么。。

 #include <stdio.h>
 #include <string.h>
 #include <algorithm>
 #include <iostream>
 const int N=;
 using namespace std;

 int main()
 {
     int t,n,p;
     cin>>t;
     while(t--)
     {
         cin>>n>>p;
         int m = *n+p;
         int cnt = ,flag = ;
         for (int i = ;i <= n; i++)
         {
             for (int j = i+;j <= n; j++)
             {
                 cout<<i<<" "<<j<<endl;
                 cnt++;
                 if (cnt==m)
                 {
                     flag = ;
                     break;
                 }
             }
             if (flag)
             break;
         }
     }
     return ;
 }