如何理解pca和svd的关系?

主成分分析和奇异值分解进行降维有何共同点？

矩阵的奇异值分解

当矩阵不是方阵，无法为其定义特征值与特征向量，可以用一个相似的概念来代替：奇异值。

通常用一种叫奇异值分解的算法来求取任意矩阵的奇异值：

抽象的概念要用具体的方式理解，来看几张图：

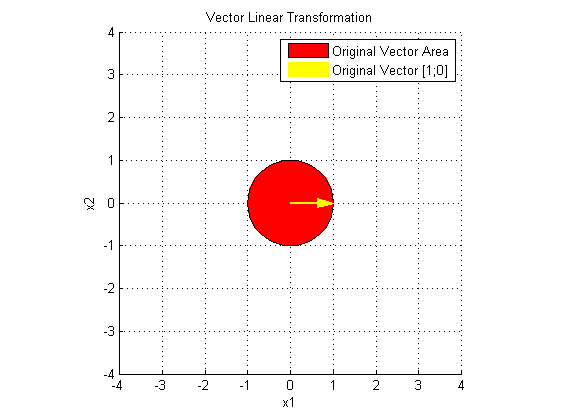
上图中的红色区域是一个以原点为中心的单位圆。圆当中的任意一点可以用向量 x 标示，且 x 满足：

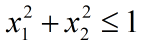
给定一个 2×2 的方阵：

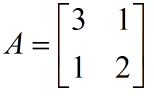
利用 MATLAB 对 A 做奇异值分解：

即：

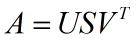
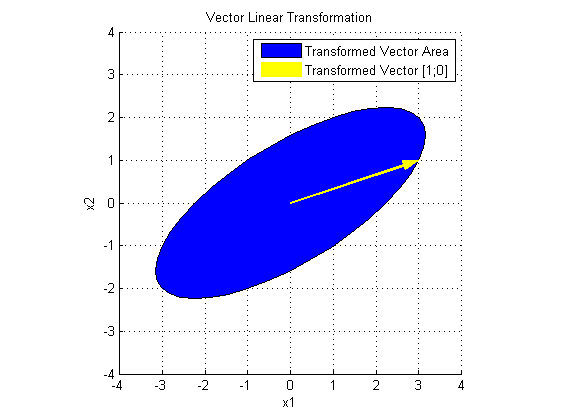
所以：

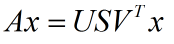
先看 V' 对 x 做了什么：

V' 使 x 旋转了一个角度。

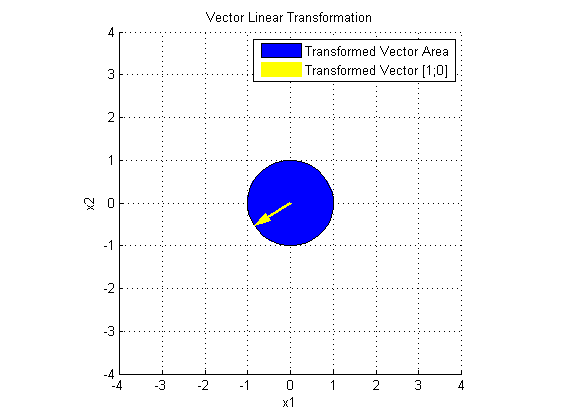
再看 SV' 对 x 做了什么：

S 在 V'x 的基础上，在两个主方向进行了伸缩变换。

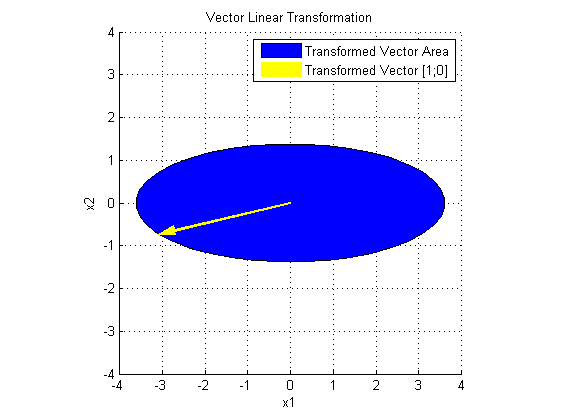
最后看 USV' 对 x 做了什么：

U 在 SV'x 的基础上，进行了旋转变换。

至此，奇异值分解的几何意义可谓一目了然：

A 是一个线性变换，把 A 分解成 USV'，S 给出了变换后椭圆长短轴的长度， U 和 V' 一起确定了变换后的方向，所以 U、S、V' 包含了这个线性变换的全部信息。S 矩阵的对角线元素称为 A 的奇异值，与特征值一样，大的奇异值对应长轴，小的奇异值对应短轴，大的奇异值包含更多信息。

当矩阵是对称方阵时，其特征值与奇异值相等。

网上有一个很经典的案例来说明 SVD 的应用：

有一张 25×15 的图片：

把它用矩阵表示：

这个矩阵的秩等于 3。即矩阵只有 3 种线性无关的列，其他的列都是冗余的：

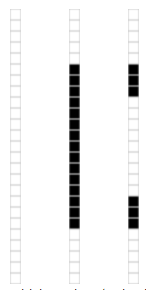
对 M 做奇异值分解，得到 3 个不为零的奇异值：

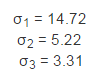
它们分别对应着 3 个线性无关的列。

另一种更一般的情况，处理一张有噪声的图片

它的奇异值为：

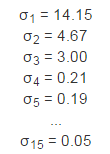
可以想象在15维空间中有一个超椭球体，它有15个轴，其中有3个轴是主要的轴（对应着3个最大的奇异值），有这3个轴就可以大致勾勒出超椭球体的形状，因为它们包含了大部分信息。

如果 S 中的对角线元素从大到小排列，我们就只保留 S 左上角的 3×3 的子矩阵，并相应保留 U 和 V 的前 3 列，简化后的 U、S、V 依然保留了 M 的大部分信息：

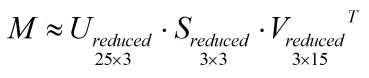
主成分分析

案例1

假如有 m 条1维数据，由于混入了噪音，变成了2维。

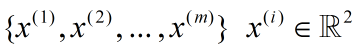
在坐标系中把他们绘制出来：

主成分分析（PCA）可以用来排除这些噪音，把原来的维度提取出来。

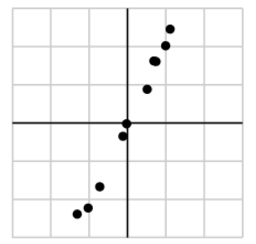
首先将数据归一化，并将其所包含的信息用 协方差矩阵（协方差矩阵表示不同维度之间的相关关系，这是一个对称矩阵）来表示：

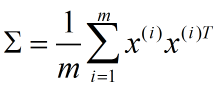
Σ 有2个奇异值，例如：

显然前者包含了大部分信息，对应的矩阵 U 的第一列就是主成分的方向：

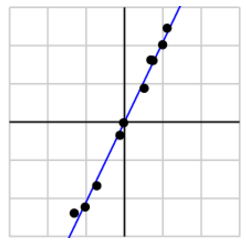
于是就通过降维对数据实现了去噪。

在更一般的情况下，假设有 m 条 n 维的数据，对协方差矩阵进行奇异值分解得到 n 个从大到小排列的奇异值：

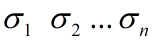
如果希望信息利用率在99%以上，可利用如下不等式来确定主成分的维度 p：

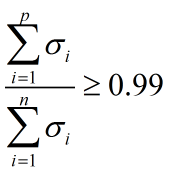
参见以下链接文章．

https://my.oschina.net/findbill/blog/535044