Codeforces Round #240 (Div. 2) D

D. Mashmokh and ACM

Mashmokh's boss, Bimokh, didn't like Mashmokh. So he fired him. Mashmokh decided to go to university and participate in ACM instead of finding a new job. He wants to become a member of Bamokh's team. In order to join he was given some programming tasks and one week to solve them. Mashmokh is not a very experienced programmer. Actually he is not a programmer at all. So he wasn't able to solve them. That's why he asked you to help him with these tasks. One of these tasks is the following.

A sequence of l integers b1, b2, ..., bl (1 ≤ b1 ≤ b2 ≤ ... ≤ bl ≤ n) is called good if each number divides (without a remainder) by the next number in the sequence. More formally 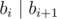 for all i (1 ≤ i ≤ l - 1).

Given n and k find the number of good sequences of length k. As the answer can be rather large print it modulo 1000000007 (109 + 7).

Input

The first line of input contains two space-separated integers n, k (1 ≤ n, k ≤ 2000).

Output

Output a single integer — the number of good sequences of length k modulo 1000000007 (109 + 7).

Sample test(s)

input

3 2

output

5

input

6 4

output

39

input

2 1

output

2

题意：给出一组数列，问满足数列递增且前一个元素能整除后一个元素的数列一共有多少种。

sl:赤裸裸的dp，比赛时叫C整的快没时间了，十分钟敲了下交了一发wa了原来忘记mod1e9了。

dp方程：  dp[i][j]+=dp[i-1][k]  (j%k==0) 只要预处理因子就可以了。

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<algorithm>
 4 #include<vector>
 5 using namespace std;
 6 const int MAX = +;
 7 const int MOD = 1e9+;
 8 int dp[MAX][MAX];
 9 vector<int> v[MAX];
 void init()
 {
     memset(dp,,sizeof(dp));
     for(int i=;i<MAX;i++) dp[][i]=;
     for(int i=;i<MAX;i++)
     {
         for(int j=;j<=i;j++)
         {
             if(i%j==) v[i].push_back(j);
         }
     }
 }
 int main()
 {
     int n,k;
     init();
     scanf("%d %d",&n,&k);
     for(int j=;j<=n;j++)
     for(int i=;i<=k;i++)
     {
         for(int m=;m<v[j].size();m++)
         {
             dp[i][j]=(dp[i][j]+dp[i-][v[j][m]])%MOD;
         }
     }
     int ans=;
     for(int i=;i<=n;i++) ans=(ans+dp[k][i])%MOD;
     printf("%d\n",ans%MOD);
     return ;

39 }