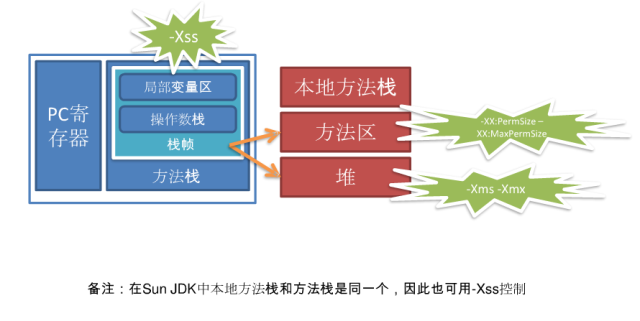
java内存组成

 java内存组成介绍：堆(Heap)和非堆(Non-heap)内存

按照官方的说法：“Java 虚拟机具有一个堆，堆是运行时数据区域，所有类实例和数组的内存均从此处分配。堆是在 Java 虚拟机启动时创建的。”“在JVM中堆之外的内存称为非堆内存(Non-heap memory)”。可以看出JVM主要管理两种类型的内存：堆和非堆。简单来说堆就是Java代码可及的内存，是留给开发人员使用的；非堆就是JVM留给 自己用的，所以方法区、JVM内部处理或优化所需的内存(如JIT编译后的代码缓存)、每个类结构(如运行时常数池、字段和方法数据)以及方法和构造方法 的代码都在非堆内存中。

组成图

• 方法栈&本地方法栈:
  线程创建时产生,方法执行时生成栈帧
• 方法区
  存储类的元数据信息 常量等
• 堆
  java代码中所有的new操作
• native Memory(C heap)
  Direct Bytebuffer JNI Compile GC;

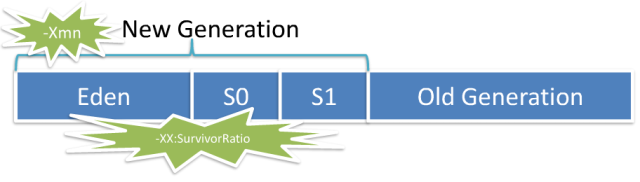
堆内存分配

JVM初始分配的内存由-Xms指定，默认是物理内存的1/64；JVM最大分配的内存由-Xmx指 定，默认是物理内存的1/4。默认空余堆内存小于40%时，JVM就会增大堆直到-Xmx的最大限制；空余堆内存大于70%时，JVM会减少堆直到 -Xms的最小限制。因此服务器一般设置-Xms、-Xmx相等以避免在每次GC 后调整堆的大小。对象的堆内存由称为垃圾回收器的自动内存管理系统回收。

组成	详解
Young Generation	即图中的Eden + From Space + To Space
Eden	存放新生的对象
Survivor Space	有两个，存放每次垃圾回收后存活的对象
Old Generation	Tenured Generation 即图中的Old Space  主要存放应用程序中生命周期长的存活对象

非堆内存分配
      JVM使用-XX:PermSize设置非堆内存初始值，默认是物理内存的1/64；由XX:MaxPermSize设置最大非堆内存的大小，默认是物理内存的1/4。

组成	详解
Permanent Generation	保存虚拟机自己的静态(refective)数据 主要存放加载的Class类级别静态对象如class本身，method，field等等 permanent generation空间不足会引发full GC(详见HotSpot VM GC种类)
Code Cache	用于编译和保存本地代码（native code）的内存 JVM内部处理或优化

JVM内存限制(最大值)

JVM内存的最大值跟操作系统有很大的关系。简单的说就32位处理器虽然 可控内存空间有4GB,但是具体的操作系统会给一个限制，这个限制一般是2GB-3GB（一般来说Windows系统下为1.5G-2G，Linux系统 下为2G-3G），而64bit以上的处理器就不会有限制了。