Luogu P4139 上帝与集合的正确用法【扩展欧拉定理】By cellur925

题目传送门

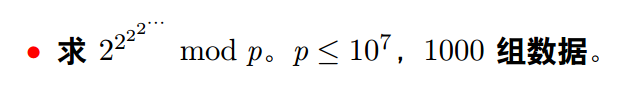
题目中的式子很符合扩展欧拉定理的样子。（如果你还不知扩展欧拉定理，戳）。对于那一堆糟心的2，我们只需要递归即可，递归边界是模数为1.

另外，本题中好像必须要用快速乘的样子...否则无法通过...。

$Code$

 #include<cstdio>
 #include<algorithm>

 using namespace std;
 const int lim=;

 int T,p;
 int phi[lim];

 void init_phi()
 {
     phi[]=;
     for(int i=;i<=lim;i++) phi[i]=i;
     for(int i=;i<=lim;i++)
         if(phi[i]==i)
             for(int j=i;j<=lim;j+=i)
                 phi[j]=phi[j]/i*(i-);
 }

 int mul(int a,int b,int mo)
 {
     int ans=;
     while(b)
     {
         if(b&) ans=(ans%mo+a%mo)%mo;
         b>>=;
         a=a%mo*%mo;
     }
     return ans;
 }

 int ksm(int a,int b,int mo)
 {
     int ans=;
     while(b)
     {
         if(b&) ans=mul(ans,a,mo)%mo;
         b>>=;
         a=mul(a,a,mo)%mo;
     }
     return ans;
 }

 int work(int mod)
 {
     if(mod==) return ;
     return ksm(,work(phi[mod])+phi[mod],mod);
 }

 int main()
 {
     init_phi();
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d",&p);
         printf("%d\n",work(p));
     }
     return ;
 }