洛谷 P5066 [Ynoi2014] 人人本着正义之名debug-log

序言

此日志分为四部分。

00:00是开始打代码的时间。

最开始打完代码（没有debug）大约用了两小时。

part1-20210323

02:30

生成新节点时，没有给随机权值。

02:41

upd中，sum更新时没有先清空，没有加上右儿子的sum。

02:46

操作12没问题

操作3会RE+WA

5 100000
0 0 0 1 1
3 1 5

change1中第7行，merge中顺序反了。

change1中第11行，分裂出的子树错误(\(z\rightarrow y\))。

03:01

split1中if(k>l[i])应为if(k>=l[i])

分裂左/右子树反了。

03:07

assign中，\(l\not=1\&\&r=n\)中\(lv[y]=x\)的case中，没有拓展同色区间。root=merge(x,node(l,n,v));改为root=merge(x,node(ll[y],n,v));

1和l看错了root=merge(root,node(1,rr[y],v));应为root=merge(root,node(l,rr[y],v));

x和1搞错了if(lv[y]!=x)应为if(lv[y]!=v)

03:10~11:40

睡觉

11:57

change1中，修改y树的根时work(y,1,flag==1?1:-1);应为work(y,0,flag?1:-1);

12:02

dfs中始终只会spread rootspread(root);改为spread(x);

12:33

spread中只要有一种标记没有打，则就不会下传标记if(!lazy[x][0]||!lazy[x][1]) return;应为if(!lazy[x][0]&&!lazy[x][1]) return;

过样例，WA+MLE+RE

12:45

hack:

5 10000
1 0 0 0 0
4 1 5

树的结构错误的变成了

1 1 1
3 5 0

操作4错误

12:55

打模拟赛

14:22

上面的错误是debug错了，输出树的结构没有spread。

15:32

忘记强制在线了，WA-ALL(说明只差一点点了！)

15:32

写了对拍(无加密)

10 100
1 1 0 1 0 0 0 1 0 0
3 3 6
5 1 4
5 4 7
7 7 8
5 5 6
3 10 10
4 6 9
3 8 9
3 5 10
7 2 9
5 6 9
6 3 10
4 1 1
1 7 7
4 4 8
2 4 7
5 5 9
1 9 9
7 1 4
5 3 4
2 2 8
2 9 10
7 8 10
2 2 7
7 3 9

我输出

1
2
2
3
7

std

1
5
4
3
7

为什么修改无效？

16:30

午餐

17:20

午休

18:12

下午好

下午没有做什么，所以暂停了计时。

18:56

晚上好。加油吧，\(Vanilla\_chan\)！

19:25

重写了upd，assign函数

/**************************************************************
 * Problem: 5066
 * Author: Vanilla_chan
 * Date: 20210323
 * E-Mail: Vanilla_chan@outlook.com
**************************************************************/
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<limits.h>
#define IL inline
#define re register
#define LL long long
#define ULL unsigned long long
#ifdef TH
#define debug printf("Now is %d\n",__LINE__);
#else
#define debug
#endif
#ifdef ONLINE_JUDGE
char buf[1<<23],* p1=buf,* p2=buf,obuf[1<<23],* O=obuf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
#endif
using namespace std;

namespace oi
{
	inline bool isdigit(const char& ch)
	{
		return ch<='9'&&ch>='0';
	}
	inline bool isalnum(const char& ch)
	{
		return (ch>='a'&&ch<='z')||(ch>='A'&&ch<='Z')||(ch>='0'&&ch<='9');
	}
	struct istream
	{
		char ch;
		bool fu;
		template<class T>inline istream& operator>>(T& d)
		{
			fu=d=0;
			while(!isdigit(ch)&&ch!='-') ch=getchar();
			if(ch=='-') fu=1,ch=getchar();
			d=ch-'0';ch=getchar();
			while(isdigit(ch))
				d=(d<<3)+(d<<1)+(ch^'0'),ch=getchar();
			if(fu) d=-d;
			return *this;
		}
		inline istream& operator>>(string& str)
		{
			str.clear();
			for(;!isdigit(ch);ch=getchar());
			while(isalnum(ch))
				str+=ch,ch=getchar();
			return *this;
		}
	}cin;
	inline int read()
	{
		int x=0,fu=1;
		char ch=getchar();
		while(!isdigit(ch)&&ch!='-') ch=getchar();
		if(ch=='-') fu=-1,ch=getchar();
		x=ch-'0';ch=getchar();
		while(isdigit(ch)) { x=x*10+ch-'0';ch=getchar(); }
		return x*fu;
	}
	int G[55];
	template<class T>inline void write(T x)
	{
		int g=0;
		if(x<0) x=-x,putchar('-');
		do { G[++g]=x%10;x/=10; } while(x);
		for(int i=g;i>=1;--i)putchar('0'+G[i]);putchar('\n');
	}
};
using namespace oi;

#define N 6000010

int n,m;
int a[N];
int root;
int key[N];
int l[N],r[N];//平衡树上一个点所代表的一段区间[l,r]
int ll[N],rr[N];//平衡树上一个点的子树代表的一段区间[ll,rr]
bool val[N];//当前点代表区间的值0/1
int ls[N],rs[N];//左右儿子
int cnt[N][2];//以当前点为根的子树内的0/1段数量
int mn[N][2];//以当前点为根的子树内，最短的0/1段的长度
int sum[N];//当前点的子树和
bool lv[N],rv[N];//当前点的子树的边界位置的值
int lazy[N][2];
int tot;
void upd(int x)
{
	if(ls[x]) ll[x]=ll[ls[x]];
	else ll[x]=l[x];
	if(rs[x]) rr[x]=rr[rs[x]];
	else rr[x]=r[x];
	cnt[x][val[x]]=1;
	cnt[x][!val[x]]=0;
	mn[x][val[x]]=r-l+1;
	mn[x][!val[x]]=n+1;
	if(val[x]) sum[x]=r[x]-l[x]+1;
	else sum[x]=0;
	if(ls[x]) lv[x]=lv[ls[x]];
	else lv[x]=val[x];
	if(rs[x]) rv[x]=rv[rs[x]];
	else rv[x]=val[x];
	if(ls[x])
	{
		cnt[x][0]+=cnt[ls[x]][0];
		cnt[x][1]+=cnt[ls[x]][1];
		mn[x][0]=min(mn[x][0],mn[ls[x]][0]);
		mn[x][1]=min(mn[x][1],mn[ls[x]][1]);
		sum[x]+=sum[ls[x]];
	}
	if(rs[x])
	{
		cnt[x][0]+=cnt[rs[x]][0];
		cnt[x][1]+=cnt[rs[x]][1];
		mn[x][0]=min(mn[x][0],mn[rs[x]][0]);
		mn[x][1]=min(mn[x][1],mn[rs[x]][1]);
		sum[x]+=sum[rs[x]];
	}
}
int node(int L,int R,bool vv)
{
	tot++;
	l[tot]=L;
	r[tot]=R;
	val[tot]=vv;
	key[tot]=rand();
	ls[tot]=rs[tot]=0;
	lazy[tot][0]=lazy[tot][1]=0;
	upd(tot);
	return tot;
}
void work(int x,bool flag,int k)
{
	//if(!x||!k) return;
	lazy[x][flag]+=k;
	if(flag)
	{
		if(val[x]) r[x]+=k;
		else l[x]+=k;
	}
	else
	{
		if(val[x]) l[x]-=k;
		else r[x]-=k;
	}
	mn[x][0]-=k;
	mn[x][1]+=k;
	sum[x]+=k*cnt[x][1];
}
void spread(int x)
{
	//if(!lazy[x][0]&&!lazy[x][1]) return;
	if(ls[x]) work(ls[x],0,lazy[x][0]),work(ls[x],1,lazy[x][1]);
	if(rs[x]) work(rs[x],0,lazy[x][0]),work(rs[x],1,lazy[x][1]);
	lazy[x][0]=lazy[x][1]=0;
}
int merge(int x,int y)
{
	if(!x) return y;
	if(!y) return x;
	if(key[x]>key[y])
	{
		spread(x);
		rs[x]=merge(rs[x],y);
		upd(x);
		return x;
	}
	else
	{
		spread(y);
		ls[y]=merge(x,ls[y]);
		upd(y);
		return y;
	}
}
void split1(int i,int k,int& x,int& y)
{
	if(!i)
	{
		x=y=0;
		return;
	}
	spread(i);
	if(k>=l[i])
	{
		split1(rs[i],k,rs[i],y);
		x=i;
	}
	else
	{
		split1(ls[i],k,x,ls[i]);
		y=i;
	}
	upd(i);
}
void split2(int i,int k,int& x,int& y)
{
	if(!i)
	{
		x=y=0;
		return;
	}
	spread(i);
	if(k<=r[i])
	{
		split2(ls[i],k,x,ls[i]);
		y=i;
	}
	else
	{
		split2(rs[i],k,rs[i],y);
		x=i;
	}
	upd(i);
}
int ask(int l,int r)
{
	int x,y,z;
	split2(root,l,x,y);//可以切多但是不能切少
	split1(y,r,y,z);//所以这里切最左侧时，应是小于当前块的右边界
	int ans=sum[y];//这样即使有可能让l在最左边的一块内部，但是下面会将多余的减去。反之同理
	if(lv[y]) ans-=l-ll[y];
	if(rv[y]) ans-=rr[y]-r;
	root=merge(x,merge(y,z));
	return ans;
}
void assign(int l,int r,bool v)
{
	int x,y,z;
	if(l==1)
	{
		if(r==n)
		{
			root=node(l,r,v);
			return;
		}
		else
		{
			split1(root,r+1,x,y);
			//if(rv[x]!=v) root=merge(merge(node(1,r,v),node(r+1,rr[x],!v)),y);
			//else root=merge(node(1,rr[x],v),y);
			if(rv[x]!=v)
			{
				root=node(1,r,v);
				root=merge(root,node(r+1,rr[x],!v));
			}
			else
			{
				root=node(1,rr[x],v);
			}
			root=merge(root,y);
		}
	}
	else
	{
		if(r==n)
		{
			split2(root,l-1,x,y);
			//if(lv[y]!=v) root=merge(x,merge(node(ll[y],l-1,!v),node(l,n,v)));
			//else root=merge(x,node(ll[y],n,v));
			root=x;
			if(lv[y]!=v)
			{
				root=merge(root,node(ll[y],l-1,!v));
				root=merge(root,node(l,n,v));
			}
			else
			{
				root=merge(root,node(ll[y],n,v));
			}
		}
		else
		{
			split2(root,l-1,x,y);
			split1(y,r+1,y,z);
			root=x;
			/*
			if(lv[y]!=v)
			{
				root=merge(root,node(ll[y],l-1,!v));
				if(rv[y]!=v)
				{
					root=merge(root,node(l,r,v));
					root=merge(root,node(r+1,rr[y],!v));
				}
				else
				{
					root=merge(root,node(l,rr[y],v));
				}
			}
			else
			{
				if(rv[y]!=v)
				{
					root=merge(root,node(ll[y],r,v));
					root=merge(root,node(r+1,rr[y],!v));
				}
				else
				{
					root=merge(root,node(ll[y],rr[y],v));
				}
			}
			root=merge(root,z);
			*/
			if(lv[y]!=v)
			{
				root=merge(root,node(ll[y],l-1,!v));
				if(rv[y]!=v)
				{
					root=merge(root,node(l,r,v));
					root=merge(root,node(r+1,rr[y],!v));
				}
				else
				{
					root=merge(root,node(l,rr[y],v));
				}
			}
			else
			{
				if(rv[y]!=v)
				{
					root=merge(root,node(ll[y],r,v));
					root=merge(root,node(r+1,rr[y],!v));
				}
				else
				{
					root=merge(root,node(ll[y],rr[y],v));
				}
				root=merge(root,z);
			}

		}
	}
}
void change1(int l,int r,bool flag)//向左传递flag
{
	int x,y,z,t;
	split1(root,l-1,x,y);
	split1(y,r,y,z);
	if(y&&lv[y])
	{
		split2(x,ll[y]-1,x,t);
		y=merge(t,y);
	}
	if(y&&!rv[y])
	{
		split2(y,rr[x],y,t);
		z=merge(t,z);
	}
	if(y)
	{
		work(y,0,flag?1:-1);
	}
	root=merge(x,merge(y,z));//FHQ-Treap常规操作
}
void change2(int l,int r,bool flag)
{
	int x,y,z,t;
	split2(root,r+1,y,z);
	split2(y,l,x,y);
	if(y&&rv[y])
	{
		split1(z,rr[y]+1,t,z);
		y=merge(y,t);
	}
	if(y&&!lv[y])
	{
		split1(y,ll[y],t,y);
		x=merge(x,t);
	}
	if(y)
	{
		work(y,1,flag?1:-1);
	}
	root=merge(x,merge(y,z));
}
int dfs(int x)
{
	//debug cout<<"x="<<x<<endl;
	spread(x);
	if(l[x]==r[x]+1) return l[x];
	else if(ls[x]&&(!mn[ls[x]][0]||!mn[ls[x]][1]))
	{
		return dfs(ls[x]);
	}
	else return dfs(rs[x]);
}
void del()
{
	int t=dfs(root);
	int x,y,z;
	split2(root,t-1,x,y);
	split1(y,t,y,z);
	root=merge(x,merge(node(ll[y],rr[y],r[y]+1==l[y]?!val[y]:val[y]),z));
}
void init()
{
	int res=1;
	for(int i=2;i<=n;i++)
	{
		if(a[i]!=a[i-1])
		{
			root=merge(root,node(res,i-1,a[res]));
			res=i;
		}
	}
	root=merge(root,node(res,n,a[res]));
}
void out(int x)
{
	spread(x);
	if(ls[x]) out(ls[x]);
	cout<<"id="<<x<<" "<<l[x]<<" "<<r[x]<<" "<<val[x]<<endl;
	if(rs[x]) out(rs[x]);
}
int op,x,y;
int lastans;

int main()
{
	freopen("5066.in","r",stdin);
	//freopen(".out","w",stdout);
	oi::cin>>n>>m;
	srand(20050228);
	for(int i=1;i<=n;i++) oi::cin>>a[i];
	init();
	while(m--)
	{
		op=read();
		x=read();
		y=read();
		//x^=lastans;
		//y^=lastans;
		if(op==1)
		{
			assign(x,y,0);
		}
		else if(op==2)
		{
			assign(x,y,1);
		}
		else if(op==3)
		{
			change1(x+1,y,1);
		}
		else if(op==4)
		{
			change2(x,y-1,1);
		}
		else if(op==5)
		{
			change2(x,y-1,0);
		}
		else if(op==6)
		{
			change1(x+1,y,0);
		}
		else
		{
			write(lastans=ask(x,y));
		}
		//out(root);
		while(!mn[root][0]||!mn[root][1]) del();
		debug
			out(root);
	}
	return 0;
}

显然这份代码不能过。能过就折寿了。

part2-20210327~20210328

在家与学校之间的地铁上debug。

upd函数中，r[x]-l[x]+1写成r-l+1。

重构代码，用指针全部重写。

\(0pts\).

part3-20210329

整个下午都在调指针。

过了自己的样例……还是\(0pts\).

又造出了一组hack数据！

debug……80pts！

数组开小了，\(3\times 10^6\)。

还是80pts……

卡常，卡常，跑完操，没吃晚饭。

找lxl小姐姐请求放大时限（然后把最后一组数据调成了8s）还是过不去。

果然，越可爱就会越毒瘤吗……

part4-20210330

进入了漫长的卡常期……

不delete废弃的指针(反正不会MLE)

把所有的==，!=都改成了^。

将while(!root->mn[0]||!root->mn[1]) update();改写到3|4|5|6内部去，减少四个if。

将随机数改写成了s*=13并\(\text{unsigned int}\)自然溢出。

spread等函数全部inline，并判断有lazy时再进入函数操作(if放到函数外面减少调用次数)。

将快读变为传址。

删除无关头文件。

split1/2中的k既不会修改也不会冲突，就去掉这个参数改为全局变量吧。

可以过\(\#27\)了！

将随机数改写成s=(s<<1)+s.等价于s*=3。

将ans变为全局变量，同时就可以不用lastans了。

对于update中的\(x\)同理。

我傻了，随机数怎么可以写成s*=3？那样对于一段内的key不久全是单调的了嘛！

换成s*=19260817。

可以过\(\#31\)了！\(90pts\)

将ask,assign,change1.change2函数中的*x,*y,*z,*t设置成全局的。

将有\(bool\)变量参数的函数全部分程两个，比如\(change1\)写成\(change10\)和\(change11\)，\(change2\)写成\(change20\)和\(change21\)，\(assign\)写成\(assign0\)和\(assign1\)，\(work\)写成\(work0\)和\(work1\)。

关于随机数，试了s=s*3^3在\(\text{unsigned short int}\)下虽然跑的很满很快，但是实际效果不如s*=19260817在\(\text{unsigned int}\)。于是我就换成了s*=1000000009在\(\text{long long}\)下的自然溢出。

考虑到读取\(3\times 10^6\)个\(\text{bool}\)变量用读取\(\text{int}\)的快读还是可圈可点的。所以写了readbool

inline void readbool(bool &xx)
{
	ch=getchar();
	while(!isdigit(ch)) ch=getchar();
	xx=ch-'0';
}

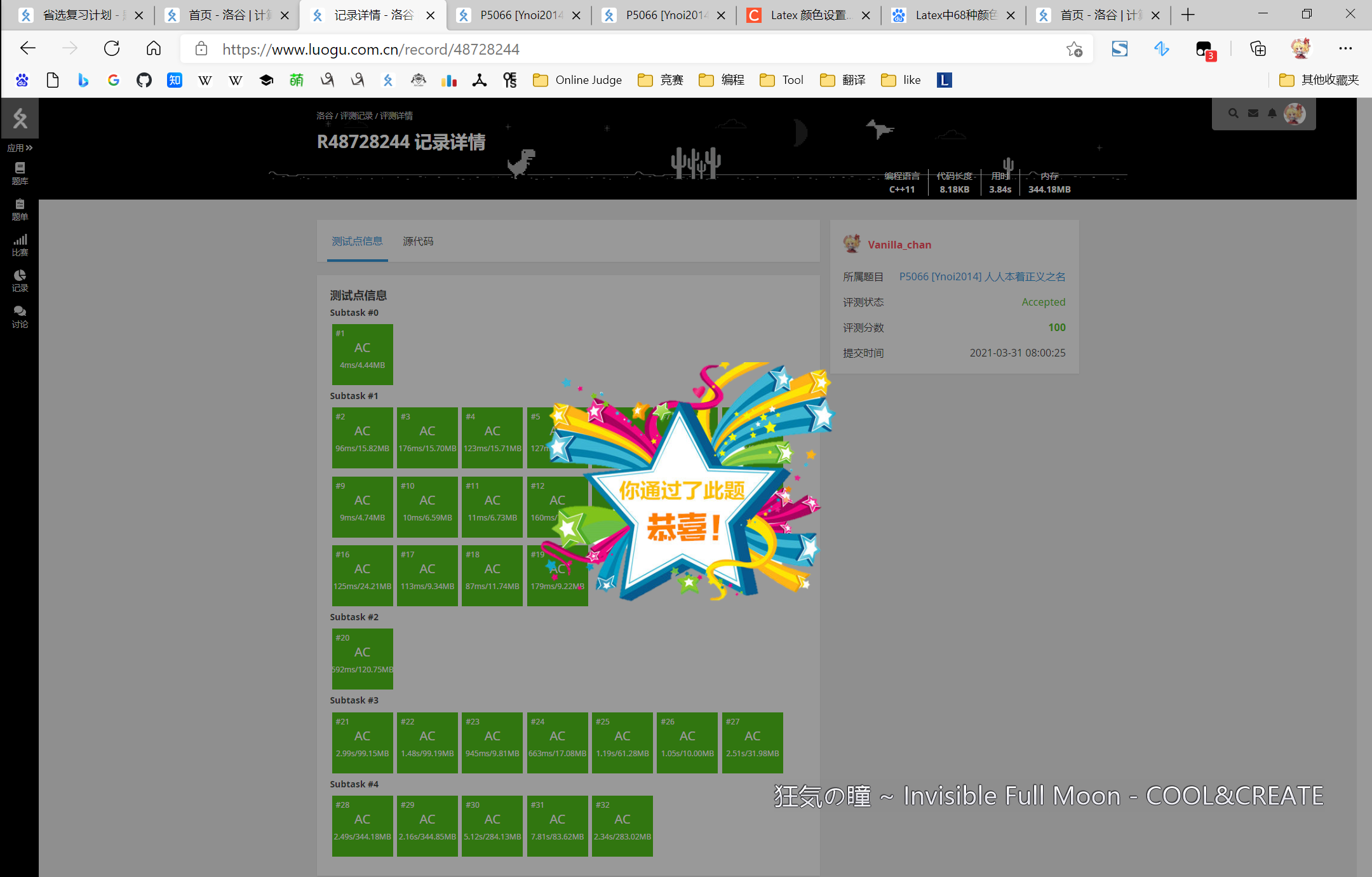
\(\textbf{2021-03-31 08:00:25 thus,AC.}\)

---

第129发过了。