Auto-Encoding Variational Bayes (VAE原文)、变分推理

　　变分自动编码器的大致概念已经理解了快一年多了，但是其中的数学原理还是没有搞懂，在看到相关的变体时，总会被数学公式卡住。下决心搞懂后，在此记录下我的理解。

公式推导——变分下界

　　这篇文章提出一种拟合数据集分布的方法，拟合分布最常见的应用就是生成模型。该方法遵循极大似然策略，即对于数据集$X = \{x^{(i)}\}^N_{i=1}$，对生成模型$p_{\theta}(x)$（注意！这里的$p_{\theta}(x)$既代表生成模型本身，又代表模型生成数据$x$的边缘概率，下面类似）完成如下优化：

\begin{align}\displaystyle \max\limits_{\theta}L = \sum\limits_{i=1}^N\log p_{\theta}(x^{(i)})\end{align}

　　但是，模型不可能凭空产生数据，必须要有输入才能有输出，所以作者对数据的生成过程进行了假设，假设数据集$X = \{x^{(i)}\}^N_{i=1}$的生成过程由以下两步组成：

　　1、通过某个先验分布$p_{\theta^*}(z)$，抽样获得隐变量$z^{(i)}$ 。

　　2、再通过某个条件分布$p_{\theta^*}(x|z)$，抽样生成$x^{(i)}$。

　　显然，以上参数$\theta^*$的值、个数，甚至是计算推演的过程，都是未知的。为了使优化得以进行，就要对参数的个数和计算流程进行约束，通常专家会根据经验来给予特定数据集特定的计算过程。不失一般性，作者假设先验分布$p_{\theta^*}(z)$和似然函数$p_{\theta^*}(x|z)$来自于参数族$p_{\theta}(z)$和$p_{\theta}(x|z)$，并且它们的概率分布函数（PDFs）几乎处处可微。换句话说，作者定义生成模型为$p_{\theta}(z)p_{\theta}(x|z)$。

　　尽管有如上假设，由于数据$x^{(i)}$与隐变量抽样$z$之间的关系未知，$p_{\theta}(x|z)$还是无法直接进行优化。于是，作者采用一种迂回的方式，让模型自己学会$z$与$x$之间的关系。作者使用自动编码器的机制，与生成模型同时训练一个后验分布模型$q_{\phi}(z|x)$，用来模拟其后验分布$p_{\theta}(z|x)$，称为编码器，并称$p_{\theta}(x|z)$为解码器。概率图如下：

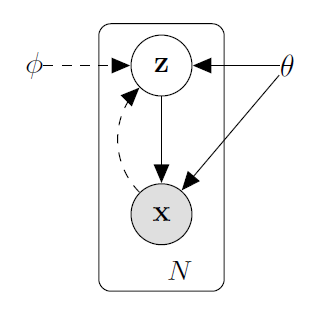
　　其中$\theta$表示生成模型$p_{\theta}(z)p_{\theta}(x|z)$的待优化参数，$\phi$表示用于估计$p_{\theta}(z|x)$的模型的参数。

　　有了$q_\phi(z|x)$作为辅助后，针对每一数据集样本$x$，待优化式可转换如下：

\begin{align} &\log p_{\theta}(x)\\ =&  \text{E}_{q_{\phi}(z|x)}\log p_{\theta}(x)\\ =&  \text{E}_{q_{\phi}(z|x)}\log \frac{p_{\theta}(x,z)}{p_{\theta}(z|x)}\\ =&  \text{E}_{q_{\phi}(z|x)}\left[ \log p_{\theta}(x,z) - \log p_{\theta}(z|x)+\log q_{\phi}(z|x)-\log q_{\phi}(z|x) \right]\\ =&  \text{E}_{q_{\phi}(z|x)}\left[ \log \frac{q_{\phi}(z|x)}{ p_{\theta}(z|x)} + \log p_{\theta}(x,z) -\log q_{\phi}(z|x) \right]\\ =& \text{KL} \left[ q_{\phi}(z|x) || p_{\theta}(z|x) \right]+ \text{E}_{q_{\phi}(z|x)}\left[ \log p_{\theta}(x,z) -\log q_{\phi}(z|x) \right] \\ =& \text{KL} \left[ q_{\phi}(z|x) || p_{\theta}(z|x) \right]+ \mathcal{L}(\theta,\phi)        \\ \end{align}

　　容易看出，由于$(8)$式第一项是相对熵非负，第二项就可看作$(2)$式的下界，称之为变分下界或证据下界（evidence lower bound, ELBO）。获得如下不等式

\begin{align}\log p_{\theta}(x) \ge \mathcal{L}(\theta, \phi)\end{align}

　　当且仅当$q_{\phi}(z|x) = p_{\theta}(z|x)$时，不等式取等。因为$p_{\theta}(z|x)$未知，第一项KL散度无法计算，又因为它有非负的性质，对优化的影响有限。所以，我们只需对$\mathcal{L}(\theta,\phi)$进行优化，原式自然变大。将$\mathcal{L}(\theta,\phi)$进行变换如下：

\begin{align} \mathcal{L}(\theta,\phi) &= \text{E}_{q_{\phi}(z|x)}\left[ \log p_{\theta}(x,z) -\log q_{\phi}(z|x) + \log_{\theta}(z) - \log_{\theta}(z) \right] \\ &= \text{E}_{q_{\phi}(z|x)}\left[ -\log q_{\phi}(z|x) + \log_{\theta}(z) + \log p_{\theta}(x,z) - \log_{\theta}(z) \right] \\ &= \text{E}_{q_{\phi}(z|x)}\left[ -\log\frac{q_{\phi}(z|x)}{p_{\theta}(z)} + \log \frac{p_{\theta}(x,z)}{p_{\theta}(z)} \right] \\ &= -\text{KL}\left[q_{\phi}(z|x)||p_{\theta}(z)\right]+ \text{E}_{q_{\phi}(z|x)}\left[ \log p_{\theta}(x|z) \right] \\ \end{align}

　　对于以上两项，我们可以把第一项理解为正则项，也就是说拟合的后验分布应该和生成模型先验分布比较接近才好；第二项理解为重构损失，就是自编码器的损失。同时对这两项进行优化，就可以使生成模型向目标靠近。

　　最终的目标函数如下：

\begin{align} \frac{1}{N}\sum\limits_{i=1}^N-\text{KL}\left[q_{\phi}(z|x^{(i)})||p_{\theta}(z)\right]+ \text{E}_{q_{\phi}(z|x^{(i)})}\left[ \log p_{\theta}(x^{(i)}|z) \right] \\ \end{align}

　　换成期望的写法：

\begin{align} \text{E}_{x\sim \mathcal{X}}\text{E}_{q_{\phi}(z|x)}\left[ -\log q_{\phi}(z|x) + \log p_{\theta}(z)+ \log p_{\theta}(x|z) \right]  \end{align}

重参数化

　　在以上优化式中包含随机采样过程，作者提出使用重参数化来建立可反向传播的采样。实际上就是给模型额外添加一个已知的随机变量作为输入，从而使模型的抽样过程可微。

　　将作者于文中对以上推导的举例——变分自动编码器（VAE），拿来与$(13)$式做对比，推导的式子以及重参数化的意义就一目了然了。其中VAE的$p_{\theta}(z)$定义为相互独立的多维高斯分布；$q_{\phi}(z|x)$对$z$的采样则是先用模型产生其方差与均值，再使用标准高斯分布的抽样重参数化获得；$p_{\theta}(x|z)$在$z$条件下对$x$的抽样，由于图像数据分布的复杂性，在实践中并没有使用重参数化，也就是解码器直接对$z$进行解码产生$x$。