模算术 modular arithmetic

https://en.wikipedia.org/wiki/Modular_arithmetic#Integers_modulo_n

模算术： 整数达到特定值时会‘ 折返 ’ 回来—— 模数 modulus（moduli）

例如： 时钟 modulo 12. 且根据定义， 12 不仅和12一致，还和0一致。

模 n 就是除数为 n 的意思。

1. 定义同余关系

　　如果  a-b=kn   那么说 a,b 是模n同余的。n为正整数，k为整数。

　　a≡b (mod n)

　　n为同余的模数。

　　同余关系写为： a=kn+b

　　a=pn+r

　　b=qn+r

　　r 为共同余数。0<=r<n

　　如 -8 ≡ 7 (mod 5)    2 ≡ -3 (mod 5)  -3 ≡ -8 (mod 5)   商可以为负数，余数一定要为 正

　　性质1： primitive root modulo n  原根模n： 如果对于与 n互质的每一个整数 a, 都存在整数 k 使得 g^k≡a (mod n) , 则 g 为原根。

　　　　n 拥有 g 当且仅当 n=2, 4, p^k,2p^k

---

2. 同余类 classes

　　' 同余模n' 是一个等价关系，整数 a 的等价类为一个集合：  $ \overline{\mathit{a}}_{n}=\left \{ \cdots , a-2n,a-n,a,a+n,a+2n,\cdots  \right \}$

　　这个集合就是 a,n 的等价类，或残余类。

---

3. 残余系统

　　整数集合 $ \left \{ 0,1,2, \cdots , n-1  \right \} $   被称为 模n的最小残余系统；

　　对于 n 个整数的集合，如果其中没有2个同余模 n ,那么被称为 模n的完全残余系统。

　　例子：

　　　　取定 n=4， 那么 ‘ 同余类 ’ 可以为：

　　　　(1)  a=1, set={ -3 ,1, 5,9,13，…}  ，余数为 1

　　　　(2) a=2, set={-2, 2, 6, 10, 14, }， 余数为 2

　　　　(3) a=3, set={ -1, 3 , 7, 11, 15}， 余数为 3

　　　　(4) a=4, set={0, 4 , 8, 12, 16}， 余数为 0

　　　　从上面4个式子中各取一个元素出来，就组合成了 ‘’ 完全残余系统‘ ； ‘其中，’ 最小残余系统‘’  为{1,2,3,4}

---

4. 约化残余系统 RRS

　　欧拉函数 φ： 输入为整数 n， 输出为小于n 且与n互质的正整数个数。

　　RRS 中的元素为 φ(n) 个，它们与 n 互质，且彼此不同余！如 n=4 时， {5,15} 为 RRS

---

5. 整数模 n  integers modulo n

　　所有 ‘ 同余类’ 的集合称为 ‘ 整数模n的环’； 也就是说， Z/nZ 里的元素还是集合，如3中的(1) (2) (3) (4)　, 共有n个

　　我们可以在这个环上定义加法，减法和乘法：

　　

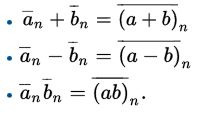
　　这些 集合 与 集合 的运算显然是成立的。

　　例如，环 Z/24Z 中 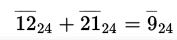    因为33除以24，余数为9

　　

　　当且仅当 n 为质数时， 这个环是个有限域。