网络编程：I/O模型

I/O模型

• Unix下可用的5种I/O模型有：
  • 阻塞式I/O
  • 非阻塞式I/O
  • I/O复用(select和poll,epoll)
  • 信号驱动式I/O
  • 异步I/O(POSIX的aio_系列函数)
• 一个输入操作通常包括两个不同的阶段：
  (1) 等待数据准备好
  (2) 从内核向进程复制数据
  对于一个套接字上的输入操作，第一步通常涉及等待数据从网络中到达。当所有分组到达时，它被复制到内核中的某个缓冲区，第二步就是把数据从内核缓冲区复制到应用进程缓冲区。

阻塞式I/O模型

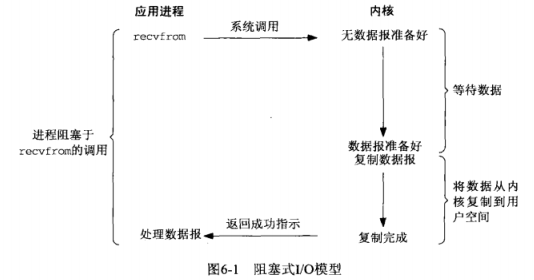
• 最流行的I/O模型时阻塞式I/O(blocking I/O)模型。默认情况下，所有套接字都是阻塞的。以数据报套接字为例：

非阻塞式I/O模型

• 进程把一个套接字设置成非阻塞是在通知内核：当所有请求的I/O操作非得把本地进程投入睡眠才能完成时，不要把本进程投入睡眠，而是返回一个错误。

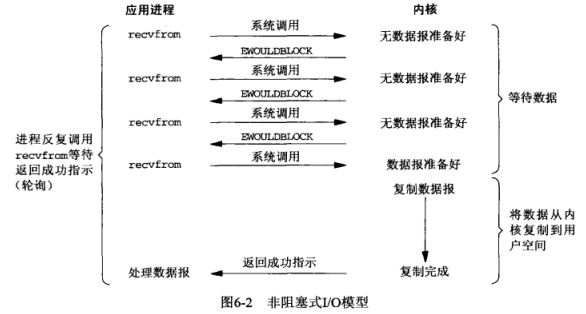
• 前三次调用recvfrom时没有数据可返回，因此内核转而立即返回一个EWOULDBLOCK错误。第四次调用recvfrom时已有一个数据报准备好，它被复制到应用进程缓冲区，于是recvfrom成功返回。我们接着处理数据。
• 当一个应用进程像这样对一个非阻塞描述符循环调用recvfrom时，我们称之为轮询(polling)。

I/O复用模型

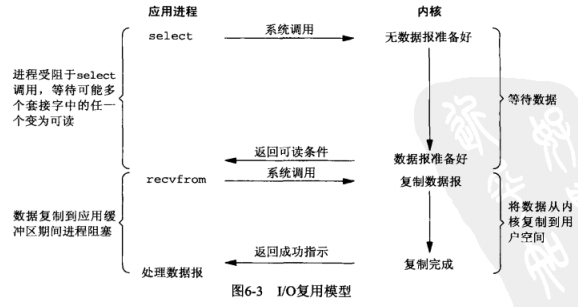
• 有了I/O复用(I/O multiplexing)，我们就可以调用select、poll或epoll，阻塞在这三个系统调用的某一个上，而不是阻塞在真正的I/O系统调用上。

信号驱动式I/O模型

• 我们也可以用信号，让内核在描述符就绪时发送SIGIO信号通知我们，称这种模型为信号驱动式I/O。

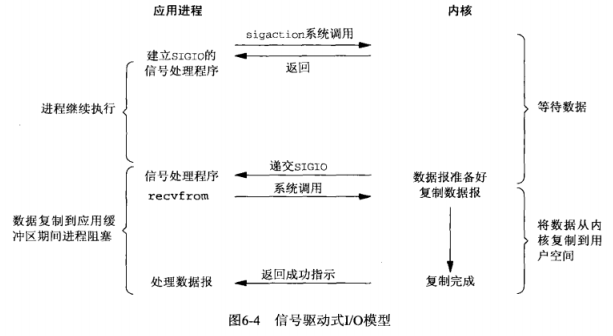
• 使用这种模型的方法：首先开启套接字的信号驱动I/O功能，并通过sigaction系统调用安装一个信号处理函数。该系统调用将立即返回，我们的进程继续工作，即进程没有被阻塞。当数据报准备好读取时，内核就为该进程产生一个SIGIO信号。我们随后可以在信号处理函数中调用recvfrom读取数据报，并通知主循环数据已准备好待处理，也可以立即通知主循环，让它读取数据报
• 无论如何处理SIGIO信号，这种模型的优势在于等待数据报到达期间进程不被阻塞。主循环可以继续执行，只要等待来自信号处理函数的通知：既可以是数据报已准备好被处理，也可以是数据报已准备好被读取。

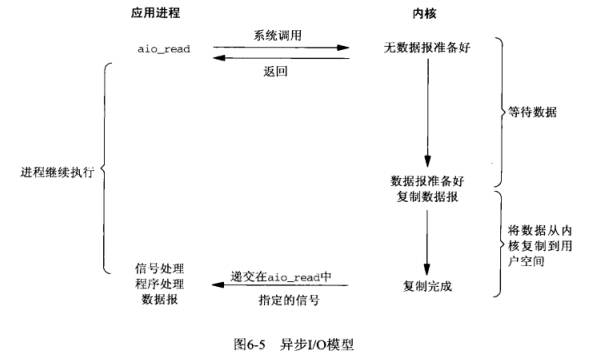
异步I/O模型

• 异步I/O(asynchronous I/O)由POSIX规范定义。演变成当前POSIX规范的各种早起标准所定义的实时函数中存在的差异已经取得一致。一般来说，这些函数的工作机制是：告知内核启动某个操作，并让内核在整个操作(包括将数据从内核复制到我们自己的缓冲区)完成后通知我们。
• 这一模型与信号驱动模型的主要区别在于：信号驱动式I/O是内核通知我们何时可以启动一个I/O操作，而异步I/O模型是由内核通知我们I/O操作何时完成。

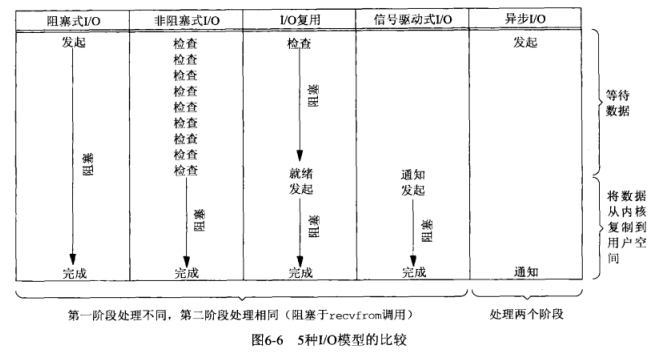
比较

• 上面所描述的5中I/O模型，前4种的主要区别在于第一阶段，因为它们的第二阶段是一样的：在数据从内核复制到调用者的缓冲区期间，进程阻塞于recvfrom调用。相反，异步I/O模型在这两个阶段都要处理，从而不同于其他4种模型。
• POSIX定义两个术语：
  • 同步I/O操作(synchronous I/O operation)导致进程阻塞，直到I/O操作完成。
  • 异步I/O操作(asynchronous I/O operation)不导致请求进程阻塞