Training Models

In this page, I am going to talk about the 'hello world' model that is linear regression and train it with 2 different ways. one is the "closed-form" equation that directly computes the model parameters that best fit the model to the training set. This method is only ok to linear regression. The other one is the Gradient Descent method(GD), that gradually tweaks the model parameters to minimize the cost function over the training set, eventually converging to the same set of parameters as the first method.

Linear Regression

Below equation 1 is the linear regression model.

Below equation 2 is the vector/matrix equation

As talked before, we have the cost function is as below.  To train a model, we have to find the value of  to minimize the RMSE/MSE

The Normal Equation

Below is the "closed-form" solution to find the model parameters that minimize the cost function.

Directly calculate the parameters:

Make a predition of 2 test data and plot the data/model: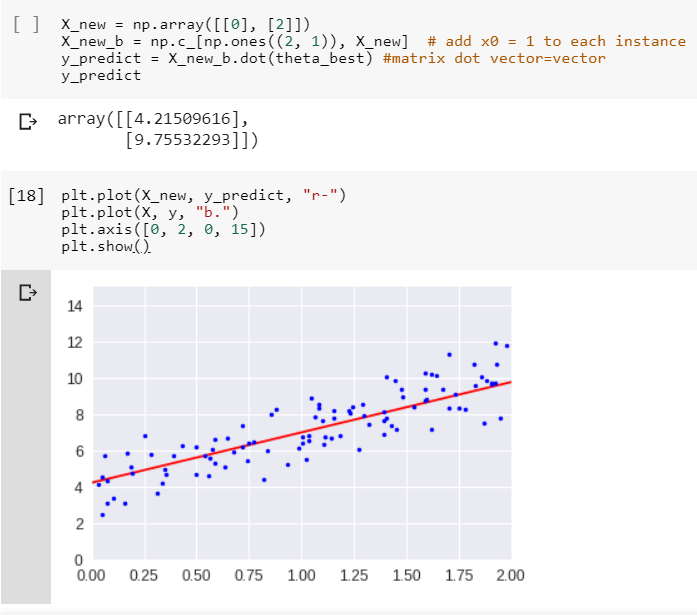

Using the sklearn lib to get the same thing:

Computational Complexity of Normal Equation

The Normal Equation computes the inverse of X.T.X, which is n*n matrix. It gets very slow when the number of features grows large(e.g., 100,000). Suggest to use it when n<=10000.

It is linear for the number of the training instances(m). The prediction is also linear with(n and m).  We will look at Gradient Descent in next article.